Awhile ago we added
GraphData[{"UnitDistance", {21, 2}}]
to Mathematica.
Graph[GraphData[{"UnitDistance", {21, 2}}], VertexLabels -> "Name"]
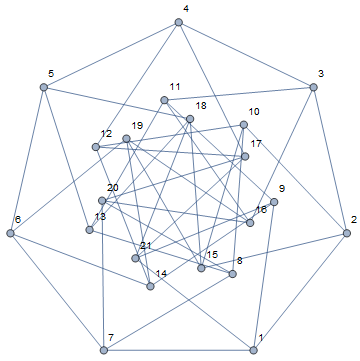
I found the graph while researching unit-distance graphs and it was an interesting enough graph to toss into GraphData.
A couple days ago I realized that this was likely a rigid graph, and thus gives a new record for bracing a heptagon. That would mean 42 edges is enough to brace the heptagon.
How to prove it? One method is to use a linkage system. If unit edge 1-7 is fixed and three thick edges of variable length are added, then all 21 points are determined. The red edges are not used in the construction process. 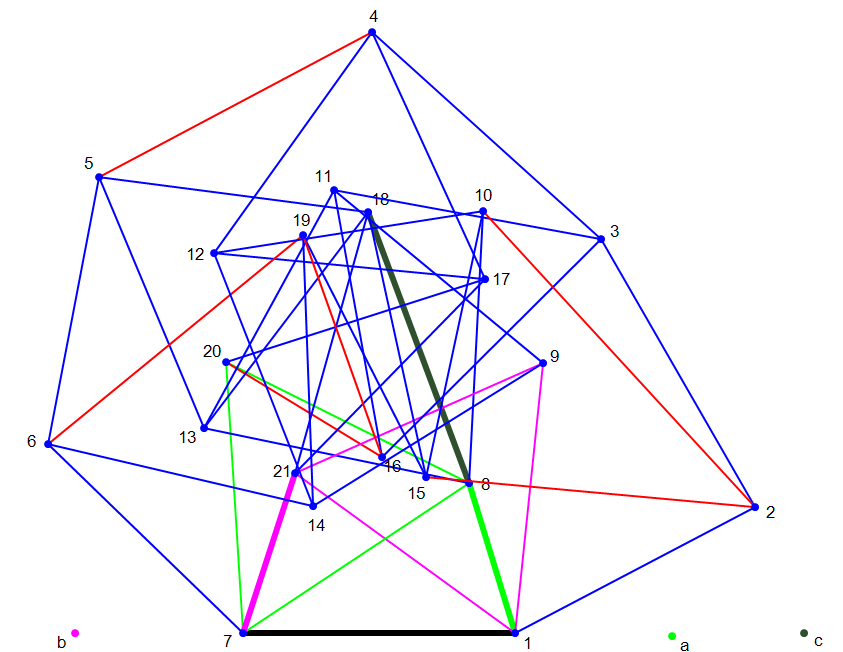
With a certain set of lengths on three variable edges, the red edges all have length 1. Adding all six red edges and removing the variable edges gives a structural rigid graph by a degrees of freedom argument. 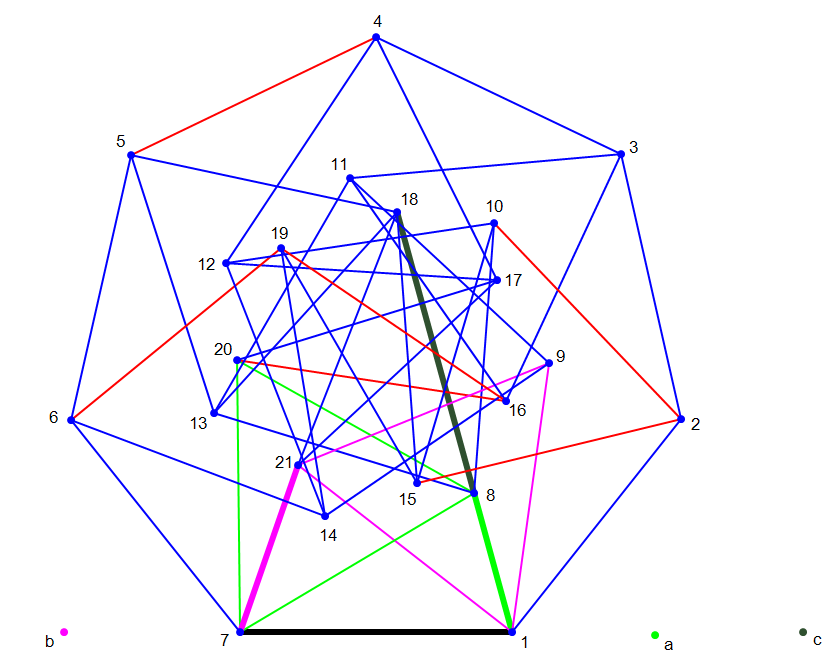
Graph coloring and rigidity seem to be interconnected. Usually, if a unit-distance graph is rigid instead of flexible, it also has chromatic number G=4. Turns out that any vertex can be deleted and the graph remains 4-chromatic. The code below verifies there are zero 3-colorings of the vertices.
ChromaticPolynomial[Select[GraphData[{"UnitDistance", {21, 2}}, "Edges"], Not[MemberQ[#, 21]] &], 3]
So theoretically, we don't need vertex 21 to brace the heptagon. That drops the bracing to 38 edges. But it seems we could toss out vertex 21 and one of the following edges and it would still be both rigid and 4-chromatic: {{4, 17}, {5, 18}, {12, 17}, {13, 18}, {15, 18}, {17, 20}}. So maybe 37 edges can brace the heptagon.
But wait! If we toss out vertex 21, it seems we can also toss out vertex 18, and it's still both 4-chromatic and rigid. So maybe just 35 edges are needed to brace the heptagon.
ChromaticPolynomial[Select[GraphData[{"UnitDistance", {21, 2}}, "Edges"], Not[MemberQ[#, 21]] && Not[MemberQ[#, 18]] &], 3]
Now we just need a rigid argument to prove it.
Many thanks to William R Somsky for assistance and the outline of a proof that 35 edges suffice. Separately, Parcly Taxel posted a different proof that 35 edges brace the heptagon.
Curiously, any two connected vertices can be removed and the graph remains rigid. But removing two non-connected vertices gives a flexible graph. I wonder if other graphs have this property.