Causal Cones are well defined in the technical introduction and in Gorard's paper on relativity: given an event (or a set of events) in the causal graph, its causal cone is the set of all the events that can be connected to it by a directed path in the causal graph. Causal cones in the Wolfram model can be directly related the concept of light cones in the theory of relativity, and this is nice.
In relativity there is a distinction between the interior of the cone, where the events are said timelike separated, and the surface of the cone, where the events are said to be lightlike separated, although still causally connected. I cannot find the same distinction in the Wolfram model.
Gorard's paper on relativity defines lightlike separated events using a discrete Minkowski norm defined on a "Minkowski lattice", but, as I have pointed out in this post, a Minkowski lattice may not be suited for the purpose because the spacetime separation of two events would be dependent on the embedding.
Even the more recent Gorard's paper Algorithmic Causal Sets and the Wolfram Model isn't (in my opinion) satisfactory regarding the concept of lightlike separation:
Two updating events may consequently be said to be causally related (i.e. connected by a directed path in the causal network) if and only if they are either lightlike-separated or timelike-separated (with lightlike separation corresponding to directed paths which lie on the boundary of discrete light cones, and all other such paths yielding timelike separations)
The problem is that I can't find an obvious way to define the boundary of a discrete light cone. To clarify what I mean, I copy here figure 8: 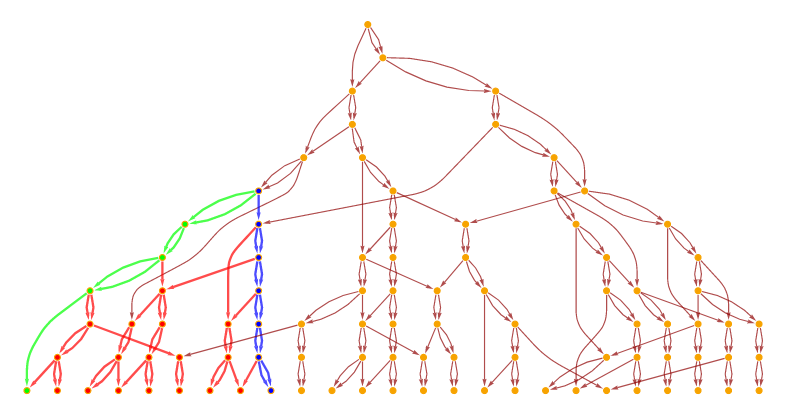
the caption says:
[...] the discrete future light cone [...] of a given updating event in the causal network [...] the two lightlike paths are highlighted in green and blue, with all other (timelike) paths shown in red.
It seems to me that the fact that the blue and green paths are on the boundary, is only due to the particular way the graph is drawn. I find no reason for which the two paths shown must necessary lie on the boundary and thus be called lightlike.
I think that if we want the causal graph to have a lorentzian manifold as limiting structure, it is important to find a good correspondence with the concept of lightlike separation in the Wolfram model. Are you aware of any way to properly define lightlike separation of events in a causal graph?