Hmmm. It looks like Piecewise, Table, and Simplify will do all of the work for you:
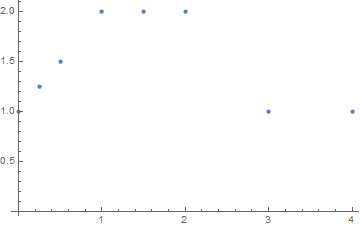
(* Make up some data *)
data = {{0, 1}, {1/4, 5/4}, {1/2, 3/2}, {1, 2}, {3/2, 2}, {2, 2}, {3, 1}, {4, 1}};
data = Sort[data, #1[[1]] <= #2[[1]] &]; (* Make sure it's sorted by the first coordinate *)
(* Define a Piecewise function *)
f[x_, data_] := Piecewise[Table[{data[[i - 1, 2]] + (x - data[[i - 1, 1]]) (data[[i - 1, 2]] - data[[i, 2]])/(data[[i - 1, 1]] - data[[i, 1]]) // Expand,
data[[i - 1, 1]] <= x <= data[[i, 1]]}, {i, 2, Length[data]}]] //Simplify
(* Use function on the data *)
g = f[z, data]

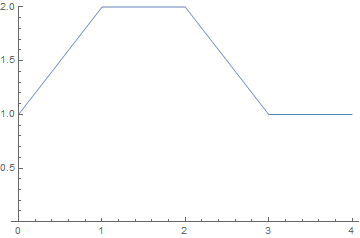
(* Plot the results *)
ListPlot[data]
Plot[g, {z, 0, 4}, PlotRange -> {Automatic, {0, Max[data[[All, 2]]]}}]