Good evening Henrik, your code looks quite good and is very fast. I think the two prominent directions are artefacts though. If I rotate the image by a random value, the peaks remain where they are. Probably the gradient function treats certain angles with a preference. This is also true for my algorithm but not to that extent. If I play with the cutoff for the refinement of the subdivision (the value 0.5 in the function "splt"), the algorithm also allows bigger deviations from the exact line, therefore also more variations in the angle of the line. I assume it is indeed a difficult issue to get a true representation of the real angular distribution, i.e. the ground truth of the underlying data, which is what we try to obtain.

We use a SEM to look at structures on a cell surface and want to test the hypothesis that they are aligned with the orientation of the tissue. First, I obtained the outline of the structures with U-Net, then I determined their center line with SkeletonTransform and Thinning. Actually I did not really phrase it correctly previously; it is not so much about finding a preferential direction but more about determining if there is an alignment with the orientation of the tissue. For this image, the anterior/posterior axis of the sample is at 18 deg, counted from the horizontal direction counterclockwise. We would assume a preference of the structures to align either parallel or perpendicular to the axis.

Good night,

Max

Hi Max,

In the end, the goal is to have a distribution of angles present in all the lines and see if there is a preference for a certain angle;

OK - new attempt! Maybe you can use GradientOrientationFilter; the result is an image consisting of the directional gradient data, ranging between -Pi/2 and +Pi/2: these data can be examined statistically (let img be the image above):

cnImg = ColorNegate@img;
gof = GradientOrientationFilter[cnImg, 3];
Histogram[gof // ImageData // Flatten, PlotRange -> {All, {0, 30000}}]

The big bar in the middle is just the background; but you see that two directions seem to be prominent.

Does that now got into the right direction? Regards -- Henrik

Hello Henrik,

I want a reduction of my line to segments, like a vectorization. So eventually I came up with this code. Maybe someone has a more elegant way of solving this, but it works, as long as it is a line without branching points.

When you skeletonize the object and remove branching points beforehand, the code works fine. Otherwise it generates a mess or errors, unfortunately.

(* example array *)
arr = {{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 1, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
1, 0, 0, 1, 0, 0}, {0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 
0, 0}, {0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0}, {0, 0,
0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}};

(* removes one point from each end and sows point *)
prune[arr_] := 
 ReplacePart[
  arr, # -> 0 & /@ 
   Sow[Position[ListConvolve[BoxMatrix[1], arr, {2, -2}, {0}]*arr, 2]]]
(* connects point to nearest end of existing chain *)
chain[c0_, m_] := 
 If[ChessboardDistance[c0[[1]], m] == 1, Prepend[c0, m], Append[c0, m]]
(* repeatedly cuts ends and connects them all together *)
lin[arr_] :=
 (
  ends = Flatten[Reap[FixedPoint[prune, arr]][[2]], 2];
  Fold[chain, {ends[[-1]]}, Drop[Reverse[ends], 1]]
  )

(* calculate distance of point from line segment, found in \
Mathematica commuity example *)
d[a_, b_, p_] := 
  If[a == b, 
   Norm[p - a], {pz, az, bz} = Map[First[#] + Last[#] I &, {p, a, b}];
    z = (pz - az)/(bz - az); 
   If[Not[0 <= Re[z] <= 1], Min[Norm[p - a], Norm[p - b]], 
    Norm[Im[z] (b - a)]]];
(* split line into two at biggest distance point, if this distance is \
bigger than 0.5 *)
splt[pts_] :=
 (
  dlst = N[d[pts[[1]], pts[[-1]], #] & /@ pts];
  p0 = Ordering[dlst, -1][[1]];
  If[dlst[[p0]] > 0.5, {Take[pts, p0], Drop[pts, p0 - 1]}, {pts}]
  )
(* flatten array with point lists *)
spltl[ptsl_] := Flatten[splt /@ ptsl, 1]
(* split list until no further change, remove double intermediates *)
lred[pts_] := Append[#[[1]] & /@ FixedPoint[spltl, {pts}], pts[[-1]]]


(* now initial split is done, then refinement of points by wiggling \
left and right *)
(* total distances in one line segment *)
sd[pts_, n1_, n2_] := 
 Plus @@ (d[pts[[n1]], pts[[n2]], #]^2 & /@ 
    pts[[Range[n1 + 1, n2 - 1]]])
(* total distances in whole line *)
ssd[pts_, nlst_] := 
 Plus @@ (sd[pts, #[[1]], #[[2]]] & /@ Partition[nlst, 2, 1])
(* wiggle each intermediate point by one left and right, find point \
list that has the minimal sum *)
ptssm[pts_, nlst_] :=
 (
  l0 = {nlst};
  (AppendTo[l0, ReplacePart[nlst, # -> nlst[[#]] - 1]]; 
     AppendTo[l0, ReplacePart[nlst, # -> nlst[[#]] + 1]]) & /@ 
   Range[2, Length[nlst] - 1];
  SortBy[l0, ssd[pts, #] &][[1]]
  )
(* repeat until no further change *)
lred1[pts_] := (pts0 = N[pts]; 
  pts0[[FixedPoint[ptssm[pts0, #] &, 
    Flatten[Position[pts0, #] & /@ lred[pts0]]]]])

Graphics[{Raster[Transpose[arr]], Red, Thick, 
  Line[# - {0.5, 0.5} & /@ lred1[lin[arr]]]}, ImageSize -> 100]

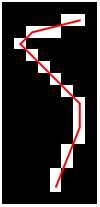
I hope that someone might find this useful.

Best, Max

Hi Max,

In the end, I want to convert the line to a vector object, ...

I am not sure about your intention, but maybe this helps:

I start with an object like this (coming from the new and useful function Canvas):

Then I basically use ComponentMeasurements to calculate the data needed for a vector representation:

img = Binarize[Image @@ obj];
cm = ComponentMeasurements[ColorNegate[img], {"Centroid", "Orientation"}];
arrows = With[{v = {Cos[#2], Sin[#2]}, l = 25}, {#1 + l v, #1 - l v}] & @@@ cm[[All, 2]];
Show[img, Graphics[{Red, Arrow /@ arrows}]]

Liebe Gruesse ins schoene Freiburg! -- Henrik