-- you have earned Featured Contributor Badge Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!

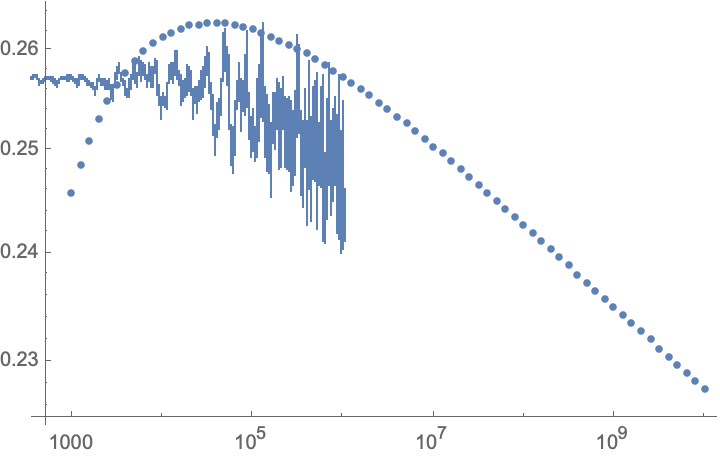
Hint: The probability to randomly hit a day with a prime factor count of 2 if the number chosen is M is about Log[Log[M]/Log[2]-1]/Log[M]. There are more exact asymptotic forms but it may get rather messy. Here a numerical comparison for this approximate probability with a numerical one when averaging over the closest 10^4 integers as a function of M:

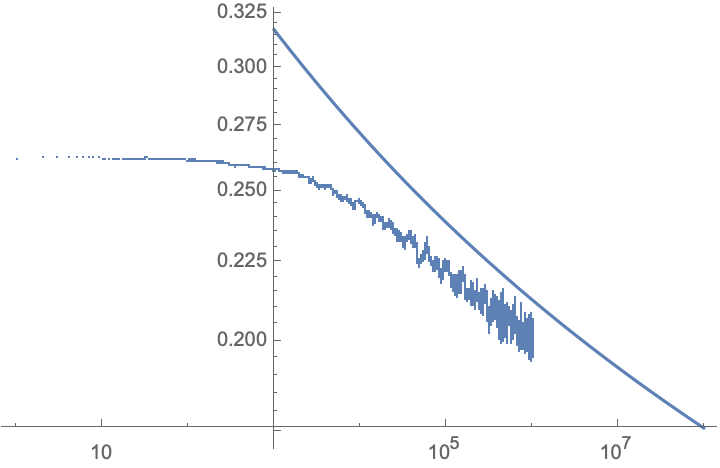
For a 3-prime factor count I cannot get out a closed form expression but an integral that can be evaluated numerically:

\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(2\), 
SuperscriptBox[\(M\), \(1/3\)]]\(\(-
\*FractionBox[\(Log[
\*FractionBox[\(Log[p]\), \(Log[
\*FractionBox[\(M\), 
SuperscriptBox[\(p\), \(2\)]]]\)]]\), \(p\ Log[
\*FractionBox[\(M\), \(p\)]]\ Log[p]\)]\) \[DifferentialD]p\)\)

and the numerical comparison is given in the following figure:

Hi Fabian,

Cool idea! I have been trying it out on extended family members birthdates.

A more functional way to generate addDays.

addDays = 
 Subsets[bDates, {2}] // Map[-DateDifference[Sequence @@ ##] & /* QuantityMagnitude]