Hi everyone! I have to solve a 2D-PDE transient heat equation that contains point heat sources. I'd like to know if I wrote the following equation correctly: 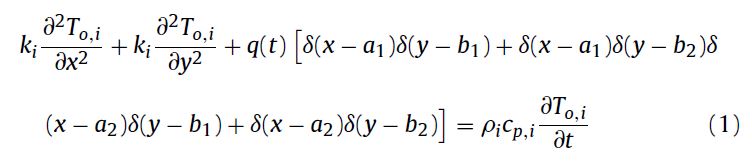
q0 = 1;
Subscript[Q, 0] =
q0*(DiracDelta[x - x1]*DiracDelta[y - y1] +
DiracDelta[x - x1]*DiracDelta[y - y2]*DiracDelta[x - x2]*
DiracDelta[y - y1] + DiracDelta[x - x2]*DiracDelta[y - y2]);
heqn1 = Subscript[k,
CLS]*(D[Subscript[T, D][x, y, t], x, x] +
D[Subscript[T, D][x, y, t], y, y]) + Subscript[Q, 0] ==
Subscript[\[Rho], CLS]*Subscript[Cp, CLS]*
D[Subscript[T, D][x, y, t], t]
I haven't considered the heat source as time-dependant just yet to simplify just a bit. Thank you in advance!