The Diffie Hellman key exchange protocol is a method for two parties to share secrets over a non-secure channel. Strength of cryptographic protection follows from the difficulty of the discrete logarithm problem (see: Guillevic & Morain, Discrete Logarithms). Industry standard implementations make use of elliptic curve addition rules, but here we will consider the simple tent map instead:

It[x_] := 1 - Abs[1 - 2 x]; (* tent map, x in [0,1] *)
ItN[x_, n_] := 1 - Abs[1 - 2 Mod[2^(n - 1) *x, 1]]; (* tent map nth power *)

After some analysis it is clear that the following equality is True:

Nest[It,x,n]==ItN[x, n] ;

If we write $\phi(x)=\phi^{1}(x)$ for the tent map, and $\phi^n(x)=\phi(\phi^{n-1}( x ) )$ as the nested tent map, we can immediately see a time savings by computing $\phi^n(x)=\phi(x,n)$ when using the alternate, function. Since we can compute $\phi(x,n)$ relatively quickly, we can in principle use it in a discrete logarithm problem where $\phi(x,n+m)=\phi(\phi(x,n),m)=\phi(\phi(x,m),n)$.

For chosen generator $g$, private key $n$ determines a public key $\phi(g,n)$. Assuming that $g=2/p$ with $p$ a safe prime (cf. A005385), then $k = p \; \phi(g,n)$ is an integer satisfying either $k = (2)^n \mod p$ or $k = - (2)^n \mod p$. The classical complexity of solving for $n$ is at best $\mathcal{O}(\sqrt{n})$ (see also: Factoring Discrete Logarithms).

First we choose a prime denominator, say $p_0=2943167$, and observe that the tent map cycle of generator $g = 2/p_0$ visits $(p_0-1)/2 = 1471583$ unique values, as is proven by a brute force check:

AbsoluteTiming[
 TentCycleGraph[pr1_] := Graph[DirectedEdge[2 #/pr1,
      It[2 #/pr1]] & /@ Range[(pr1 - 1)/2]];
 pr = Prime[2^17 + 2^16];
 dat = ConnectedComponents[TentCycleGraph[pr]];
 Length /@ dat]

which returns the correct number in about 10 seconds. The integer $1471583$ is also the size of the key space, while the 10 second time figure gives some idea how fast the inverse function could possibly be computed. In all practical applications, a much larger keyspace would be necessary.

Before moving on to key-exchange, let us take a look at the distribution of $k$ vs $n$ :

AbsoluteTiming[ invdat = MapIndexed[{pr #1, #2[[1]]} &, NestList[It, 2/pr, len - 1]];]
Histogram3D[invdat, Boxed -> False]

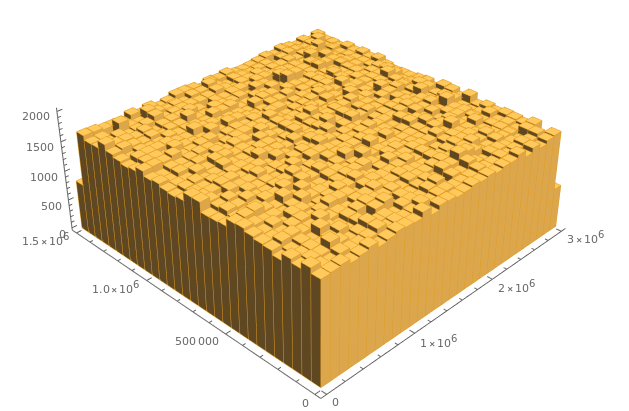
The distribution is almost normal, which indicates good dispersion of public key values, and also reaffirms the difficulty of finding inverse values.

Now for the easy part. In secret, Alice and Bob both choose integer-valued keys $n$, and generate public keys using $\phi(2/p,n)$:

AbsoluteTiming[{
KeyA = RandomInteger[{10^5, 10^6}],
 PubA = pr*ItN[2/pr, KeyA]}]
AbsoluteTiming[{
KeyB = RandomInteger[{10^5, 10^6}],
   PubB = pr*ItN[2/pr, KeyB]}]

For example, Alice has $n=392085 \rightarrow \phi = 1105606$ while bob has $n=956058 \rightarrow \phi = 2735806$. Both $\phi$ keys are passed through an unencrypted public channel. A third party, an eavesdropper name Eve, intercepts both $1105606$ and $2735806$. Meanwhile, secret values $392085$ or $956058$ do not enter the public channel, so Eve can not find either value without inverting $\phi$ (easy enough with a small keyspace, but difficult in general). Alice and Bob can then compute $p \; \phi(1105606/p,956058) = p \; \phi(2735806/p,392085) = 2257734$, a shared secret key.

In practice, Alice and Bob both own and operate small, black box mail servers, which are inconspicuously addressed online. After symmetric key exchange, the friends can then use SMTP to send encrypted messages. There is no problem with contemplative, inquisitive Eve, who deals with exclusion by going back to nature and writing poetry. While Eve is pacifistic, we can readily expect the existence of many more aggressive adversaries who even hate nature poety. So it really is important for Alice and Bob (and Eve) to invest time and effort in securing their devices.