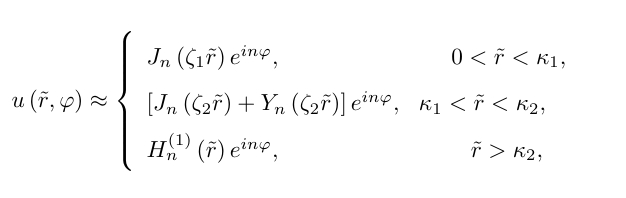
Hello, I try to prepare this function for plotting, but it appeared more difficult than expected. I have written the following code for the three respective functions on the image:
u3[r_, \[Phi]_] := BesselJ[r, n]*Exp[I n phi], {r, 0, 0.5}, {\[Phi], 0, 2 \[Pi]}, {n, 0, 5};
u4[r_, \[Phi]_] := (BesselJ[3*r, n] + BesselY[3*r, n])*Exp[I n phi], {r, 0.5, 1}, {\[Phi], 0, 2 \[Pi]}, {n, 0, 5};
u5[r_, \[Phi]_] := HankelH1[r, n]*Exp[I n phi], {r, 0.5, 10}, {\[Phi], 0, 2 \[Pi]}, {n, 0, 5};
Then I was going to make a function W which sums the three together, and then plot W.
But I get an error over and over again for the Bessel and Hankel formulation. Based on the image given, where zeta 1 and 2 are constants, what is wrong here?
Any help appreciated!