Hi Alex,
Thanks for changing the filename this time. The code in testt.nb 16-06-35-484.nb works fine for me. Make sure you start from a clean kernel. The problem is with the plotting because NIntegrate will be called hundreds of times. You can speed up the integration like this
B[u_?NumericQ] :=
NIntegrate[(1 - c*g)*h[t]/K + g*(1 - c*g)*(1 - h[t]/K) - (h[t])/K, {t, A, u},
Method -> {Automatic, "SymbolicProcessing" -> 0}]
Then this is pretty fast
Plot[Exp[B[u]], {u, 0, 250}]
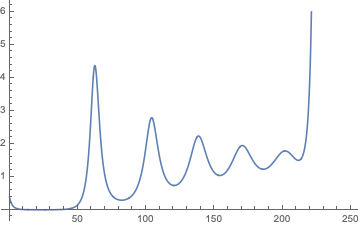
Looks like the integral starts diverging around x = 225. Please verify that the change to B to speed it up is not impacting accuracy.