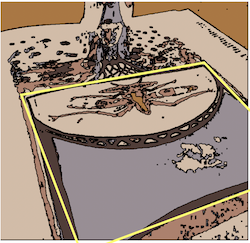
Self-anamorphism is when an image is equal to its reflection. As demonstrated in my previous community contribution, this is is only possible in a conical mirror. In a cylindrical mirror one can have "double images" when both the image and its reflection are recognizable figures. The surrealist artist Salvador Dalí experimented with these remarkable optical illusions to create ambiguous images. A good example is "Anamorphosis Harlequin" (Insect and Clown or "Papillon Fantastique") of 1972. Here we see a "double image": the image of an insect reflected as a harlequin or clown face in a cylindrical mirror.

To discover the reflection of Dalí's artwork, the above image needs a perspective correction. I used the method from the article "The Ambassadors" by Andrew Moylan. The coordinates of a deformed rectangle were obtained using the finder in Mathematica's "Drawing Tools". The resulting geometric transformation to straighten the rectangle was applied it to the image of the insect:
ImageGraphics[im]
{p1, p2} = {{{80.3, 450.6}, {484, 525}, {684, 214}, {217.8,
3.32}}, {{80.3, 450.6}, {600, 450.6}, {600, 0}, {80.3, 0}}};
tf = Last@
FindGeometricTransform[p1,
p2]; ImagePerspectiveTransformation[im, tf]

This shows the reflection of the above image in a cylindrical mirror and an enlarged detail showing the harlequin face:

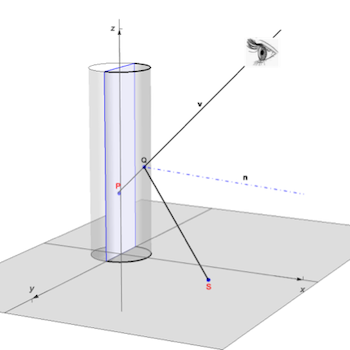
To analyse Dalí's method and find some new applications, we need the mathematics of reflection and anamorphism in a cylindrical mirror. The following two functions map anamorphic points S into reflected points P (and vice-versa) using 3D geometry and the law of reflection. They are simplified versions of the functions used in my Wolfram Demonstrations: Cylindrical Mirror Anamorphosis and Cylindrical Anamorphosis of Some Popular Images.
anamorph[{yp_,
zp_}, \[Phi]_ : \[Pi]/
4.] := {yp (3 - 2 yp^2 +
2 Sqrt[1 - yp^2] zp Cot[\[Phi]]), -2 (1 - yp^2)^(
3/2) - (zp - 2 yp^2 zp) Cot[\[Phi]]}
reflect[{xs_, ys_}, \[Phi]_ : \[Pi]/4.] :=
First[Select[{yi, zi} /.
Solve[{xs,
Abs@ys} == {yi (3 - 2 yi^2 + 2 Sqrt[1 - yi^2] zi Cot[\[Phi]]),
2 (1 - yi^2)^(3/2) + (zi - 2 yi^2 zi) Cot[\[Phi]]}, {yi, zi}],
Last[#1] > 0 &]]
Let's first test these functions on a square and a circle to see the deformations between the anamorphic images in the x-y plane and their corresponding reflection in a cylindrical mirror centered at the z-axis:
polyRadius[t_, r_, m_] :=
r Cos[Pi/m] Sec[(2 ArcTan[Cot[(1/2) m (t - Pi/4)]])/m]
Module[{polyA, anaPoly, polyR, reflectPoly},
polyA = Table[
AngleVector[{0, 3}, {polyRadius[t, .8, 4], t}], {t, 0., 2 Pi,
Pi/50}];
anaPoly = anamorph /@ polyA /. {x_?NumericQ, y_} :> {-y, x, 0.01};
polyR = Table[
AngleVector[{0, 4.5}, {polyRadius[t, 2.4, 4], t}], {t, 0., 2 Pi,
Pi/50}];
reflectPoly =
reflect[#] & /@ polyR /. {y_?NumericQ, z_} :> {0.01, 1.5 y, z};
GraphicsRow[Map[Graphics3D[{
{Opacity[0.5], Gray,
InfinitePlane[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}]},
{Opacity[.01], LightGray, Cylinder[{{0, 0, 0}, {0, 0, 5}}, 1]},
{Opacity[.15], FaceForm[Lighter[Blue, .9]],
Polygon[{{0, -1, 0}, {0, -1, 5}, {0, 1, 5}, {0, 1, 0}}]},
{FaceForm[Darker[Yellow, .15]],
EdgeForm[{Blue, AbsoluteThickness[4]}],
Polygon /@ #}}] &, {{polyA /. {y_?NumericQ, z_} :> {.01, y, z},
anaPoly}, {polyR /. {y_?NumericQ, z_} :> {z, y, .01},
reflectPoly}}]]]
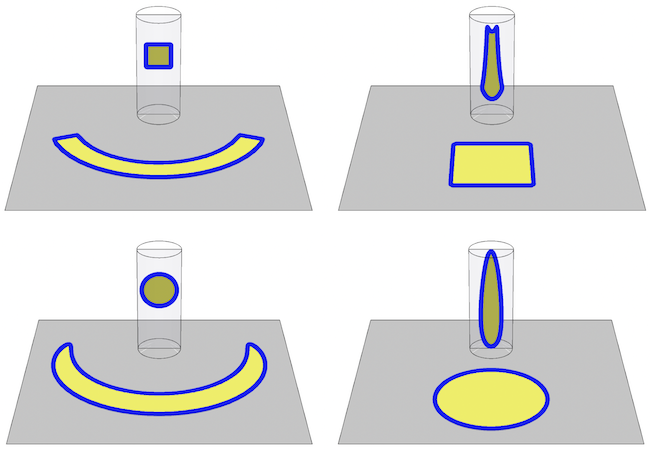
To the left is an anamorphic image reflecting as a square (top) or a circle (bottom) in a cylindrical mirror. To the right is the reflected image of a square (top) or a circle (bottom) in a cylindrical mirror. Straight lines reflect as curves and certain curves reflect as straight lines! Let us now find out if a face reflects as an insect and some insect reflects as a face?
face = With[{e0 = 1.75`, e1 = 1.4, e2 = 1.4, e3 = 0.45, hLine = 0.5,
ptc0 = 1.75, ptc1 = {-0.45, 2}, ptc2 = {0.45, 2},
ptc3 = {0, 0.75}, ptl = 1.45, ptm = -0.07, ptt = {0., 1.5},
rc0 = 0.92, rc1 = 0.2, rc2 = 0.2, rc3 = 0.35, rLine = 0.5,
rl = 0.7, rm = 0.75, rt = 0.25, n = 50},
Module[{hat, eyes, head, nose, brow, moust, pupilL, pupilR, line},
eyes =
MapThread[
Table[#1 + #2 {Cos[t], #3 Sin[t]}, {t, 0, 2 Pi,
Pi/n}] &, {{ptc1, ptc2, ptc3}, {rc1, rc2, rc3}, {e1, e2,
e3}}]; line = (#1 + {0, hLine} &) /@
Table[{x, rLine}, {x, -.5, .5, 0.01}];
head = Table[{0, ptc0} + rc0 {Cos[t], e0 Sin[t]}, {t, 0, 2 Pi,
Pi/n}]; nose =
Table[AngleVector[ptt, {polyRadius[t, rt, 3], t}], {t, 0, 2 Pi,
Pi/n}]; brow = (#1 + {0, ptl} &) /@
SortBy[RandomPoint[
Line[{{-0.5 rl, 1}, {0, 0.5/rl}, {0.5` rl, 1}}], n], First];
moust = (#1 + {0, ptm} &) /@
SortBy[RandomPoint[
Line[{{-0.5 rm, 1}, {0, +0.8/rm}, {0.5` rm, 1}}], n], First];
pupilL = CirclePoints[ptc1 - {0, 0.75` rc1}, .5 rc1, n];
pupilR = CirclePoints[ptc2 - {0, 0.75` rc2}, .5 rc2, n]; {head,
Sequence @@ eyes, nose, brow, moust, pupilL, pupilR}]];
insect = With[{e1 = 0.25, e2 = 0.25, e3 = 1, e4 = 1, etr = 4.9,
ets = 0.9, htb = -3.75, htm = -2.75, htr = -3.5, hts = -2.5,
ptc1 = {-1.05, -3.25}, ptc2 = {1.05, -3.25},
ptc3 = {-0.75, -3.25}, ptc4 = {0.75, -3.25}, rb = 1., rc1 = 0.9,
rc2 = 0.9, rc3 = 0.15, rc4 = 0.15, rm = 1, rtr = 0.16, rts = 0.4,
n = 50},
Module[{torso, trunk, wings, moust, brows},
trunk =
Table[{0.01`, htr} + rtr {Cos[t], etr Sin[t]}, {t, 0, 2 Pi,
Pi/n}]; torso =
Table[{0.01`, hts} + rts {Cos[t], ets Sin[t]}, {t, 0, 2 Pi,
Pi/n}]; wings =
MapThread[
Table[#1 + #2 {Cos[t], #3 Sin[t]}, {t, 0, 2 Pi,
Pi/n}] &, {{ptc1, ptc2, ptc3, ptc4}, {rc1, rc2, rc3,
rc4}, {e1, e2, e3, e4}}];
moust = (#1 + {0, htm} &) /@
SortBy[RandomPoint[Line[{{-rm, 0}, {0, -0.2`/rm}, {1 rm, 0}}],
n], First];
brows = (#1 + {0, htb} &) /@
SortBy[RandomPoint[Line[{{-rb, -0.2`}, {0, 0}, {rb, -0.2}}], n],
First]; {torso, trunk, Sequence @@ wings, moust, brows}]];
Grid[{Style[#, Bold] & /@ {"face", "insect"},
Graphics[{Thick, Line /@ #}] & /@ {face, insect}}]
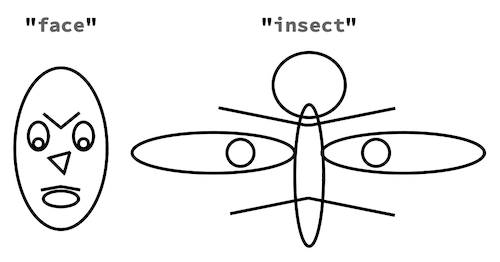
As a test, this code shows the reflection of an undeformed face:
scaledFace = Map[ScalingTransform[{3.5, 0.525}, {0, 7}], face, {2}];
reflectedFace = Map[reflect, scaledFace, {2}];
Graphics3D[{
{Opacity[0.5], Gray,
InfinitePlane[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}]},
{Opacity[.15], LightGray, Specularity[1, 2],
Cylinder[{{0, 0, 0}, {0, 0, 4}}, 1]},
{Opacity[.15],
Polygon[{{0, -1, 0}, {0, -1, 4}, {0, 1, 4}, {0, 1, 0}}]},
{Red, Thick, Line /@ reflectedFace /. {x_, y_} -> {0, x, y - 1},
Line /@ face /. {x_, y_} -> {y, x, 0}}}]
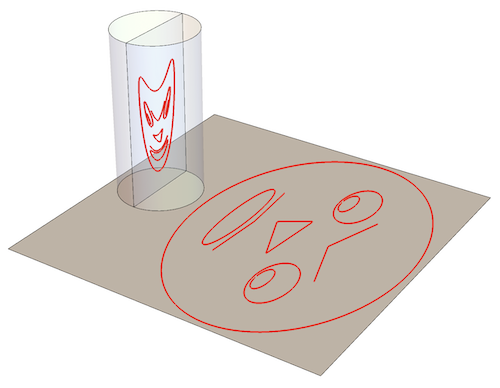
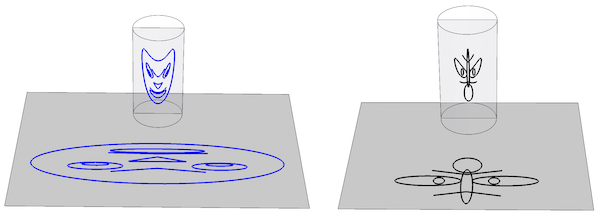
With variations of the above code, one can test the 4 possible combinations face/insect with anamorphic/reflected:
Using the function reflect: how does the reflection of a face (L) or a insect (R) look in a cylindrical mirror?
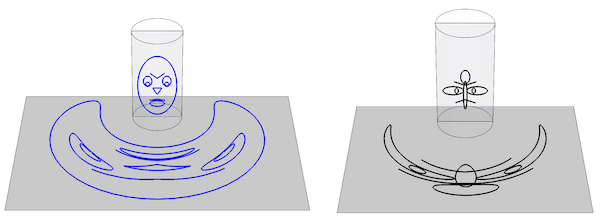
Using he function anamorph: what reflects as a face (L) or a insect (R) in a cylindrical mirror?
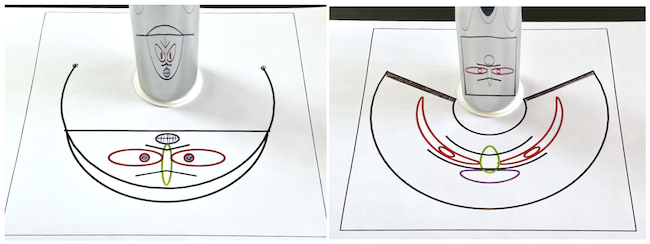
Applying some color, we can make printouts of both face and butterfly combining the anamorphic image with their computed reflections:
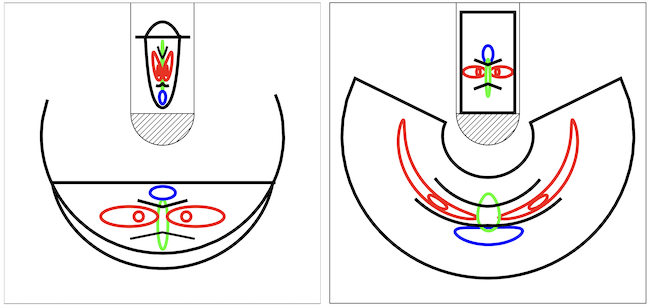
The definitive test is to try these out in a setup with a real cylindrical mirror:
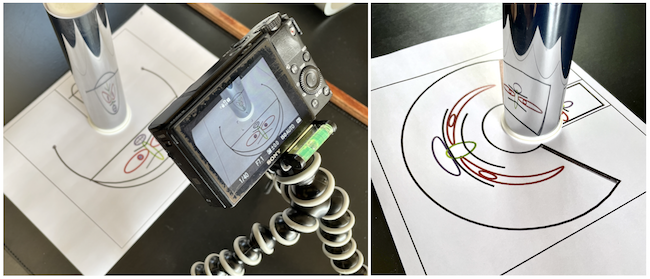
Here is the result of the reflection in a home made cylindrical mirror. Not as artistically beautiful as Dalí's but fun to do ...and cheaper than the original! (lithographs of his "Anamorphosis Suite" of 1972 sell for around 6,000 Euro)