As it well known, Lanczos algorithm is unstable in general case. For stabilization we can use the Gram-Schmidt process to orthogonalize intermediate set of vectors. So we can use two step algorithm. First, we precompute with the Lancozs algorithm as follows
A = {{1, 2, 3}, {2, 4, 5}, {3, 5, 6}};
n = Length[A];
q0 = RandomInteger[{-1, 1}, n];
q[1] = q0/Norm[q0, 2]; r[0] = q[1]; b[0] = 1.;
q[0] = ConstantArray[0, n]; k = 0;
Do[If[b[k] != 0, q[k + 1] = r[k]/b[k], Break[]];
k = k + 1; a[k] = (q[k] . A) . q[k];
r[k] = ((A - (a[k]*IdentityMatrix[n])) . q[k]) - (b[k - 1]*q[k - 1]);
b[k] = Norm[r[k], 2];, {k, 0, 2 n}]
Second, we use orthogonalization and put condition for break
Do[If[b[k] != 0., q[k + 1] = r[k]/b[k], Break[]];
k = k + 1; a[k] = (q[k] . A) . q[k];
r[k] = ((A - (a[k]*IdentityMatrix[n])) . q[k]) - (b[k - 1]*q[k - 1]);
ort = Orthogonalize[Table[r[k - n + i], {i, n}],
Method -> "GramSchmidt"]; Do[r[k - n + i] == ort[[i]];, {i, n}];
b[k] = Norm[r[k], 2]; id = k;
If[Sqrt[Sum[(a[k - 2 n + i] - a[k - n + i])^2, {i, n}]] < 10^-5,
Break[], Continue[]];, {k, n + 1, 100 n^2}]
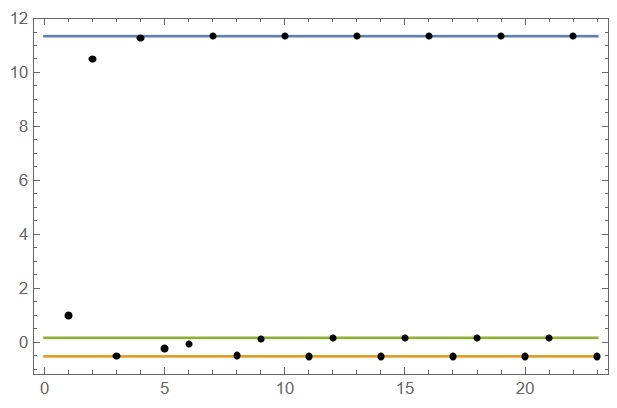
In the next example we take (by random choice) q0={-1, 1, -1}. In this case number of iterations is id=23, and the result of the last 2n iterations is
Table[{a[k], q[k]}, {k, id - 2 n + 1, id}] // TableForm
We can compare result for eigenvalues with standard function Eigenvalues[] as follows
{Sort[Table[a[k], {k, id - n + 1, id}]],
val = Eigenvalues[A // N] // Sort}
Out[]= {{-0.515729, 0.170912, 11.3448}, {-0.515729, 0.170915,
11.3448}}
Finally we plot result on every iteration to check convergence
Show[Plot[val, {x, 0, id}, Frame -> True, Axes -> False],
ListPlot[Table[a[k], {k, 1, id}], PlotRange -> All,
PlotStyle -> Black]]