For me the exclusion command appears to work:
Plot[1/(1 + x), {x, -2, 2}, Exclusions -> (1 + x) == 0]
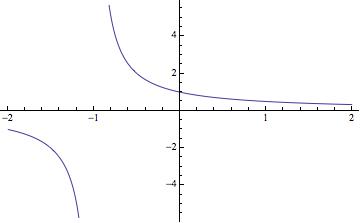
and
Plot[1/Sin[x], {x, 0, 15}, Exclusions -> Sin[x] == 0]
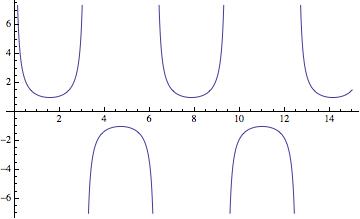
Or even more challenging:
Plot[1/Sin[1/x], {x, -1, 1}, Exclusions -> Sin[1/x] == 0,
PlotRange -> {All, {-20, 20}}]
M