Hi Wolfram community!
So here's my situation. I wrote a simple code that plots the dielectric function / optical constants using a multi-oscillator Lorentz equation. To verify my code, I tried running it using known parameters that have also shown the resulting dielectric function / optical constants. However, the plots I'm getting from the code is a bit different from the correct plots. The shape of the curves are the same. However, values are not 100% correct. it is a little bit off. Also, for the imaginary part, the plot is negative even when the correct answer must be positive. I just want to ask what could be the possible reason why the solution I'm getting from my code is like this?
Here's my code:
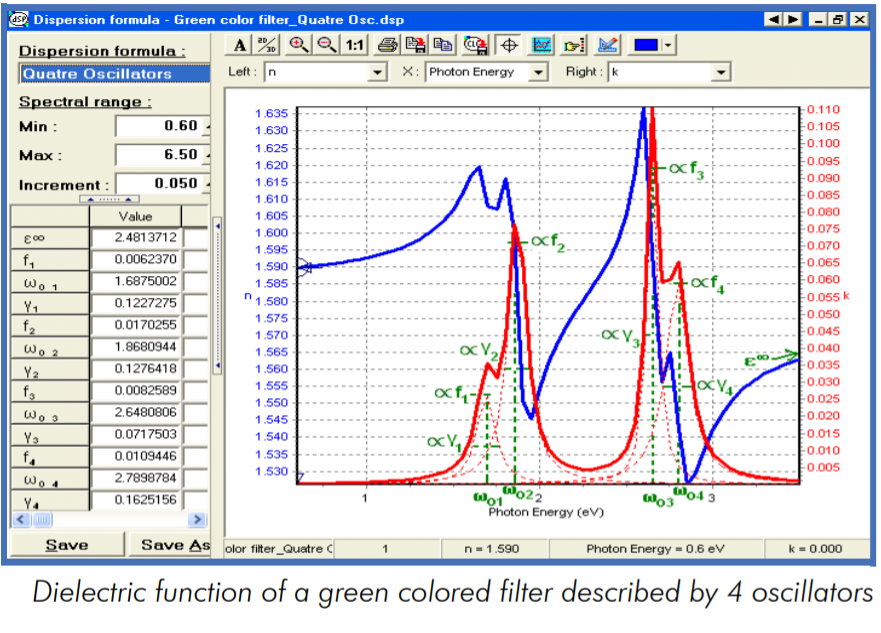
n = 2.481; (*Einf*)
c1 = 0.00623; (*amplitude*)
a1 = 1.687; (*resonant energy (eV)*)
b1 = 0.122; (*damping coefficient*)
c2 = 0.0170;
a2 = 1.868;
b2 = 0.127;
c3 = 0.00825;
a3 = 2.648;
b3 = 0.0717;
c4 = 0.0109;
a4 = 2.789;
b4 = 0.162;
model1[x_] :=
Sqrt[ n + ((c1)/((a1*a1) - (x*x) + (I*b1*x))) + ((c2)/((a2*a2) - (x*
x) + (I*b2*x))) + ((c3)/((a3*a3) - (x*x) + (I*b3*
x))) + ((c4)/((a4*a4) - (x*x) + (I*b4*x)))]
Plot[Re[model1[x]], {x, 0.60, 6.50}, PlotLabel -> "n vs. energy"]
Plot[Im[model1[x]], {x, 0.60, 6.50}, PlotLabel -> "k vs. energy"]
Thank you in advance for helping me!
Edit: I've also put the resulting plots and the reference plot here: Plots from Mathematica code: 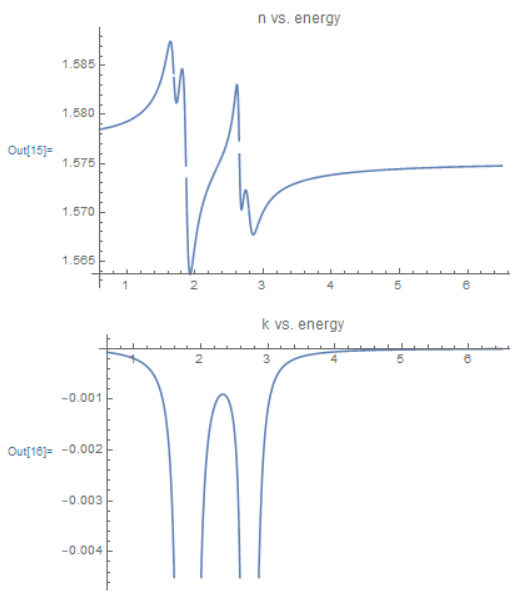
Reference plot (From Horiba's Lorentz Dispersion Model)