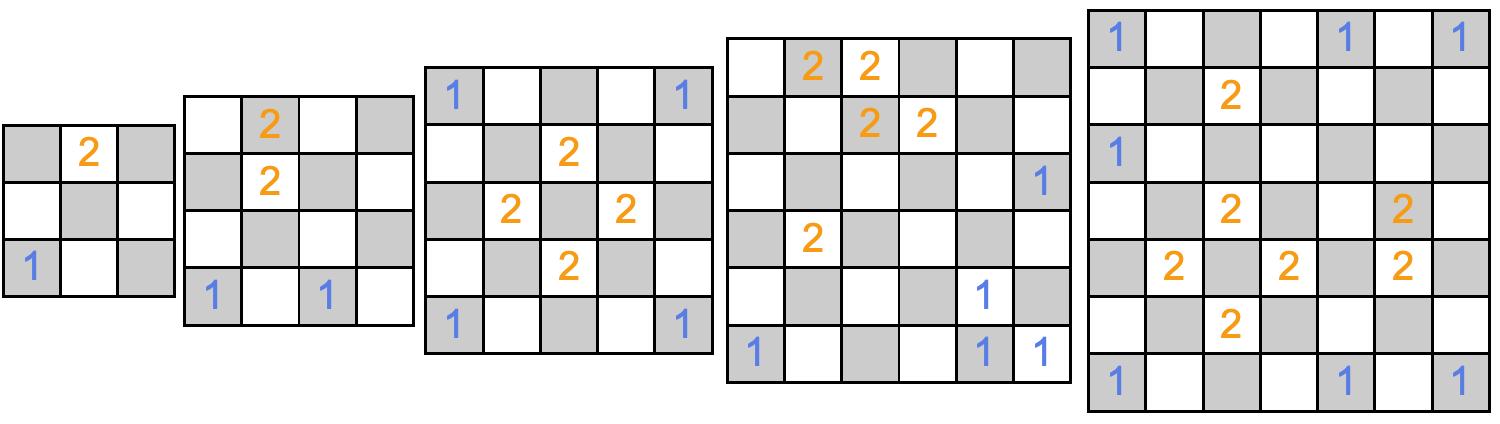
I was solving the Rosetta problem Peaceful chess queen armies just now. The idea is to place q armies of queens, each m large, on a n-by-n chess board such that one army of queen can not capture any other queen. The task there ask us to place 2 armies of each 4 queens on a 5*5 board:
ClearAll[ValidSpots, VisibleByQueen, SolveQueen, GetSolution]
VisualizeState[state_] := Module[{q, cells, colors,},
colors = DeleteCases[Union[Flatten@state[[All, All, "q"]]], -1];
colors = Thread[colors -> (ColorData[106] /@ Range[Length[colors]])];
q = MapIndexed[
If[#["q"] == -1, {},
Text[Style[#["q"], 20, #["q"] /. colors], #2]] &, state, {2}];
cells =
MapIndexed[{If[OddQ[Total[#2]], FaceForm[],
FaceForm[GrayLevel[0.8]]], EdgeForm[Black],
Rectangle[#2 - 0.5, #2 + 0.5]} &, state, {2}];
Graphics[{cells, q}, ImageSize -> Length[First@state] 30]
]
ValidSpots[state_, tp_Integer] := Module[{vals},
vals =
Catenate@
MapIndexed[
If[#1["q"] == -1 \[And] DeleteCases[#1["v"], tp] == {}, #2,
Missing[]] &, state, {2}];
DeleteMissing[vals]
]
VisibleByQueen[{i_, j_}, {a_, b_}] :=
i == a \[Or] j == b \[Or] i + j == a + b \[Or] i - j == a - b
PlaceQueen[state_, pos : {i_Integer, j_Integer}, tp_Integer] :=
Module[{vals, out},
out = state;
out[[i, j]] = Association[out[[i, j]], "q" -> tp];
out = MapIndexed[
If[VisibleByQueen[{i, j}, #2], <|#1,
"v" -> Append[#1["v"], tp]|>, #1] &, out, {2}];
out
]
SolveQueen[state_, toplace_List] :=
Module[{len = Length[toplace], next, valid, newstate},
If[len == 0,
tmp = state;
Print[VisualizeState@state];
Abort[];
,
next = First[toplace];
valid = ValidSpots[state, next];
Do[
newstate = PlaceQueen[state, v, next];
SolveQueen[newstate, Rest[toplace]]
,
{v, valid}
]
]
]
GetSolution[n_Integer?Positive, m_Integer?Positive, numcol_ : 2] :=
Module[{state, tp},
state = ConstantArray[<|"q" -> -1, "v" -> {}|>, {n, n}];
tp = Flatten[Transpose[ConstantArray[#, m] & /@ Range[numcol]]];
SolveQueen[state, tp]
]
GetSolution[5, 4, 2]
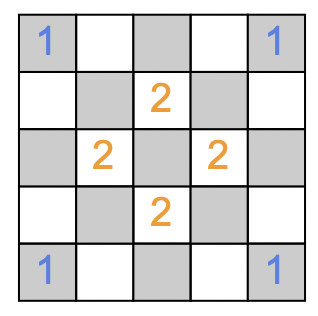
Notice that no queen of army 1 can capture any queen of army 2 (and vice versa).
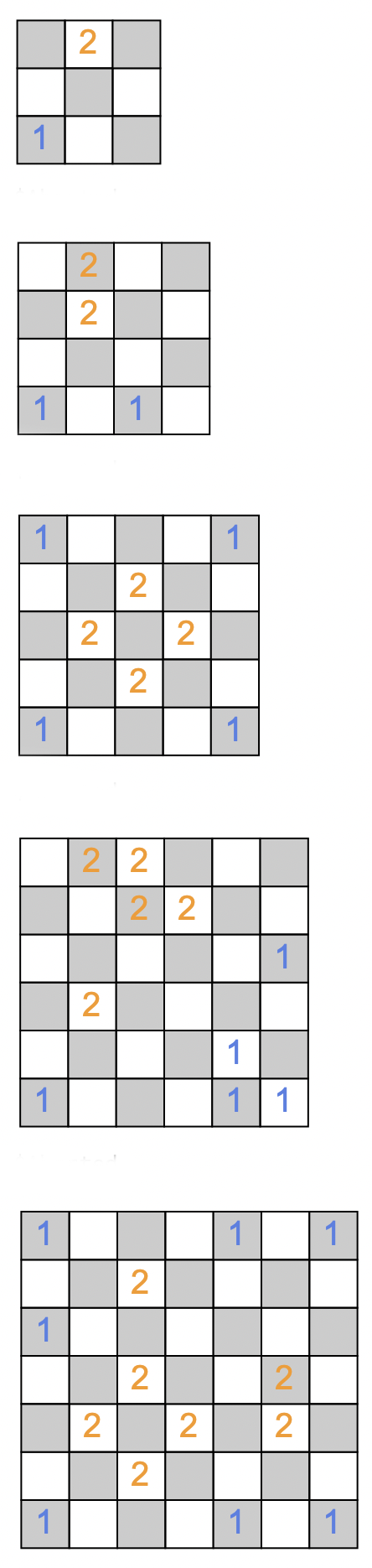
But we can go much beyond that, let;s check what can happen for a given chess board size how many we can place for the case of 2 armies:
GetSolution[3, 1]
GetSolution[4, 2]
GetSolution[5, 4]
GetSolution[6, 5]
GetSolution[7, 7]
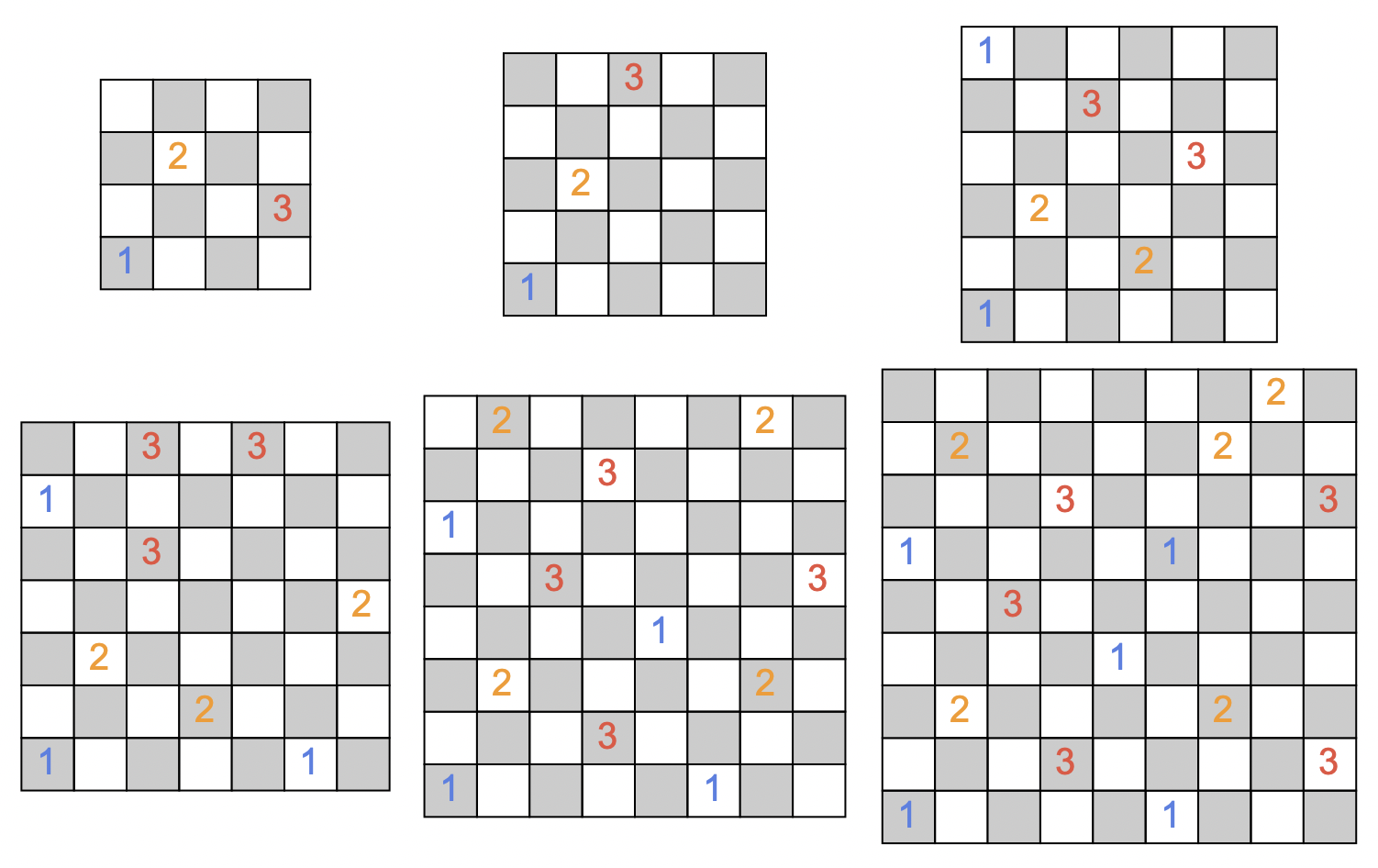
We can also look at more than 2 armies, let's look at 3 armies:
There are many more things to explore: not only square chessboard but also rectangular chessboard, more colors, other chess pieces…