Message Boards Message Boards

GROUPS:
Mathematics Mathematica Graphics and Visualization Optimization
Viktoriya Martynyuk-Lototska

Finding minimum value of function (interval mathematics)

Viktoriya Martynyuk-Lototska
Posted 9 years ago
7019 Views
|
4 Replies
|
1 Total Likes
|
Hi! I must find minimum of function as follows.
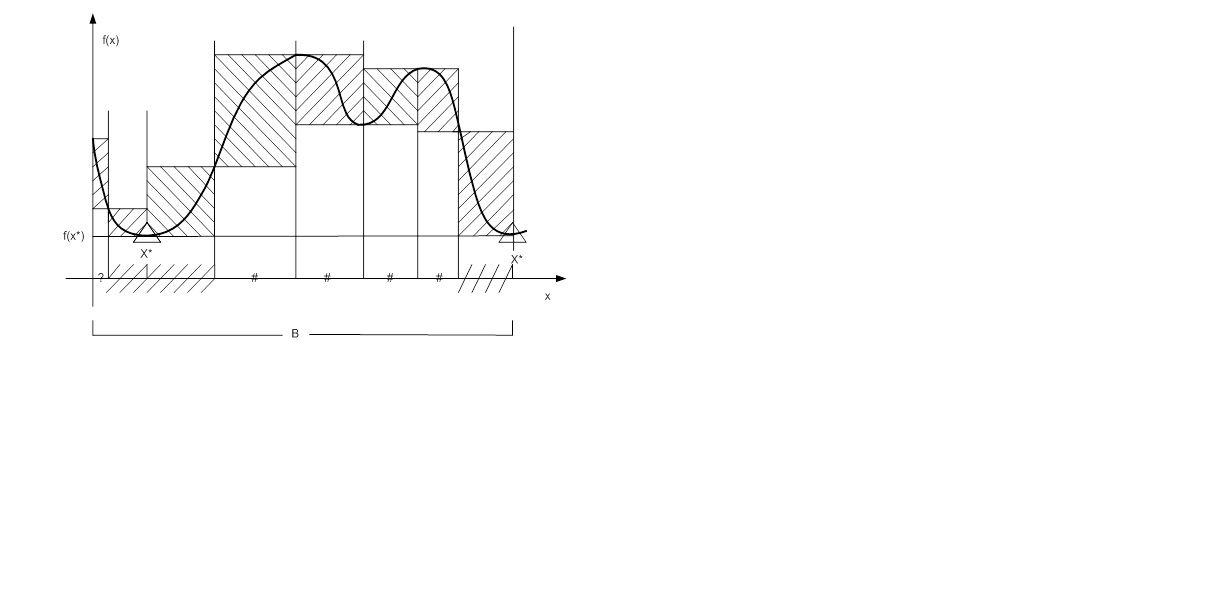
For example, I have such a graphic I saw that there are two points of minimum and some of rectangles are exactly higher than others, so I need discard them and continue only with the remaining rectangles.

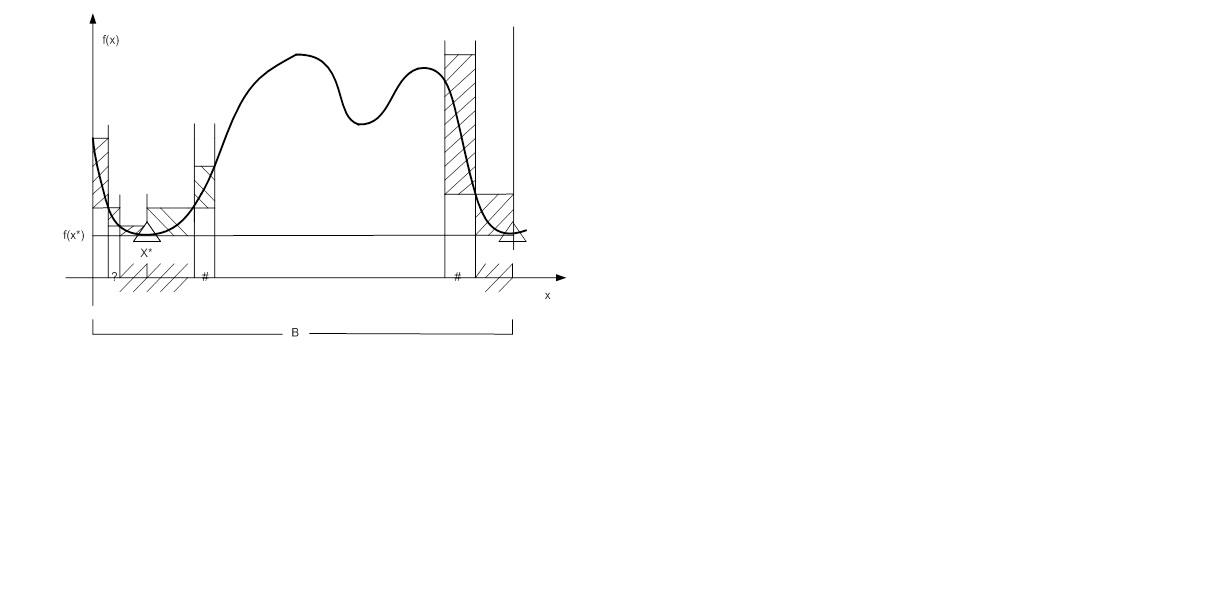
If I can't see exactly which rectangles are higher I must divide my interval on more rectangles. 
Thanks,
Viktoriya.
P.S. I know how draw rectangles on a function:
gr[f_, xmin_, xmax_, slices_] :=
 Module[{span = (xmax - xmin)/slices, ext},
  ext[op_, r_] := First@Quiet@op[{f[x], r <= x <= r + span}, x];
  Plot[f[x], {x, xmin, xmax},
   Prolog -> {FaceForm[Gray], EdgeForm,
     Rectangle @@@ ({{#, ext[Minimize, #]}, {# + span,
           ext[Maximize, #]}} & /@ Most@Range[xmin, xmax, span])}]];
f[x_] := x + 3*Sin[x + 2]; gr[f, -5, 5, 10]
POSTED BY: Viktoriya Martynyuk-Lototska
4 Replies
Sort By:
David Keith
David Keith
Posted 9 years ago
I have found that NMinimize and NMaximize are reasonably good at finding the global extremum if the method used is "SimulatedAnnealing" or "RandomSearch" but not so good with the default method.
In[20]:= f = (x - 1)^2 + 5 Sin[x];

In[21]:= NMinimize[f, x, Method -> "SimulatedAnnealing"]

Out[21]= {-0.348, {x -> -0.779015}}
POSTED BY: David Keith
Stan Wagon has written global optimization code that works via intervals. Below are a couple of references.

http://www-sbras.nsc.ru/interval/Library/Surveys/ThinkGlobally.pdf?PHPSESSID=df71c15e5c2bcf30c47aeb0f975ed2cc

http://www.mathematica-journal.com/issue/v9i3/newpublications/ISBN089871561X.html
POSTED BY: Daniel Lichtblau
You should first find all the stationary points of the function.
FindRoot[f'[x]==0,x]
Then check each x to identify maxima and minima and identify largest maximum.  Can use
Max[x1,x2,...]
POSTED BY: S M Blinder
The notation might be a bit confusing. I suppose that x1, x2 etc are the x-coordinates of the extrema. If that is so to determine the global maximum one might want to calculate
Max[f[x1],f[x2],...] (*This is not Mathematica notation*)
Perhaps this is better:
f[x_] := x + 3*Sin[x + 2];
Solve[D[f[x], x] == 0, x]
and then
f[x] /. {{x -> -2 - ArcCos[-(1/3)]}, {x -> -2 + ArcCos[-(1/3)]}}f[x] /. {{x -> -2 - ArcCos[-(1/3)]}, {x -> -2 + ArcCos[-(1/3)]}}

(*{-2 - 2 Sqrt[2] - ArcCos[-(1/3)], -2 + 2 Sqrt[2] + ArcCos[-(1/3)]}{-2 - 2 Sqrt[2] - ArcCos[-(1/3)], -2 + 2 Sqrt[2] + ArcCos[-(1/3)]}*)

But I don't think that this answers Victoriya's questions. 

M.
POSTED BY: Marco Thiel
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract