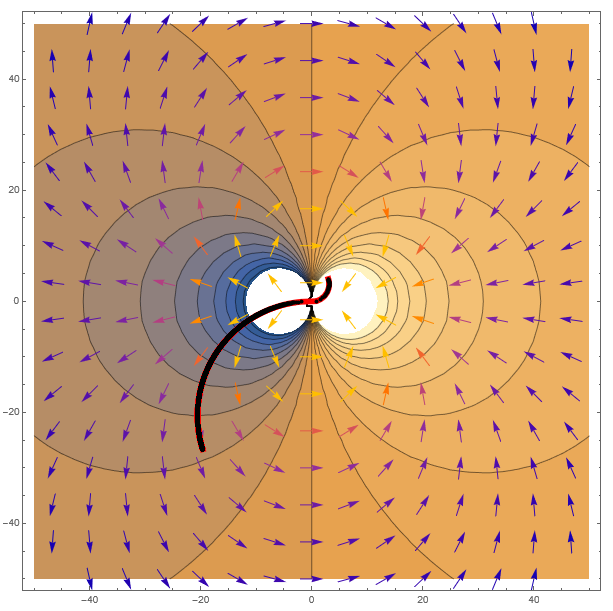
Is this what you want?
Clear[x, y];
fun = x/(x^2 + y^2);
grad = Grad[fun, {x, y}];
gradFunc = grad /. Thread[{x, y} -> N[{##}]] &;
stepFunc = (#1 + #2 gradFunc @@ #1) &;
nSteps = 8000;
stepSize = 2;
startPoint = {3, 4};
points = NestList[stepFunc[#, stepSize] &, startPoint, nSteps];
rr = 50;
Show[
ContourPlot[fun, {x, -rr, rr}, {y, -rr, rr}, AxesLabel -> Automatic,
ImageSize -> 600],
VectorPlot[gradFunc[x, y], {x, -rr, rr}, {y, -rr, rr},
VectorScale -> {.03, 1, None}, VectorPoints -> Automatic],
Graphics[{Red, Thickness[.01], Line[points]}],
Graphics[{Black, PointSize[Medium], Point[points]}]
]