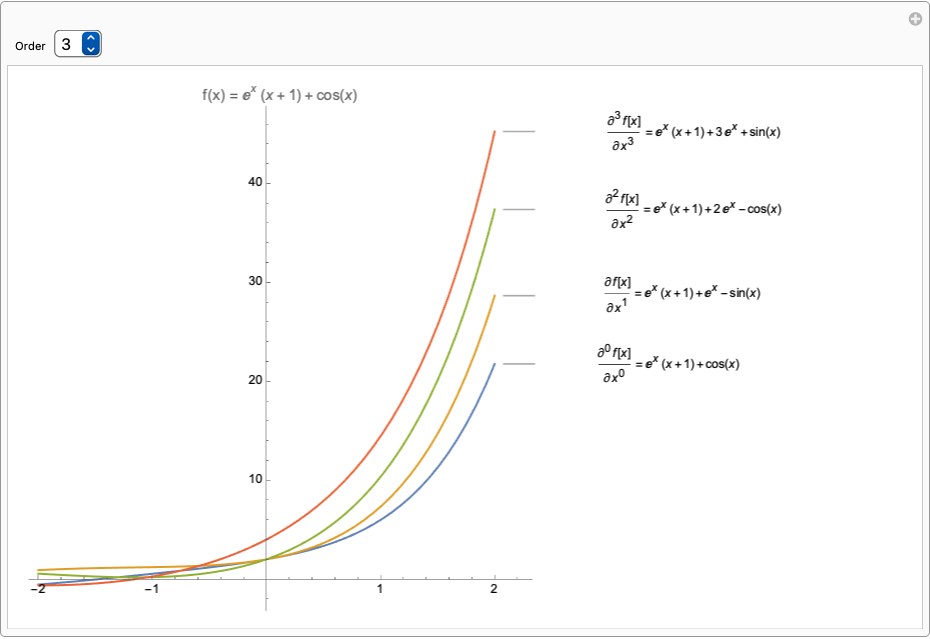
If you know how to differentiate then it is quite clear from the labels which order each curve corresponds to. Both can be displayed but the labels become long and high. The code is quite messy, good practice for you to refactor it to make it cleaner. Maybe you just want to display a number corresponding to the order rather than the differential operator, you can easily change the code to do that. Or maybe add a Tooltip to show the order, there are many possibilities....
Manipulate[
Refresh[
functions = Table[D[f[x], {x, n}], {n, 0, nMax, 1}];
orders =
Table[D[f[x], {x, n}] // Inactivate // TraditionalForm // ToString, {n, 0, nMax, 1}];
labels = MapThread[#1 <> " = " <> ToString[#2, TraditionalForm] &, {orders, functions}];];
Plot[functions, {x, -2, 2},
PlotLabels -> labels,
PlotRange -> All,
ImageSize -> 700,
AspectRatio -> 1,
PlotLabel -> Row[{"f(x) = ", f[x]}]],
{{nMax, 1, "Order"}, 1, 5, 1, PopupMenu}]