It takes a long time to learn all of the commands in Mathematica.
For the Boltzmann distribution do you want a plot of the number of states for each energy? Here's how to do that. Use
Tuples to generate a list of all possible states. Then
Map (/@) the command
Total across the list to transform each state into its energy. Then
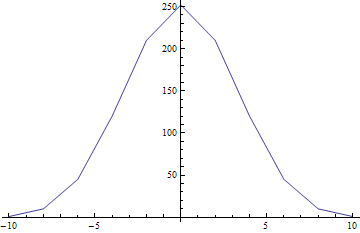
Tally the number of times each energy appears and plot it.
ListLinePlot@Tally[Total /@ Tuples[{-1, 1}, 10]]
 MatrixPlot
MatrixPlot does allow you to label the steps, but you can only choose the colors for the squares for each neutron state. It's pretty easy to just replace each 1 or -1 with an up or down arrow and show those in a
GraphicsGrid though. Here's how to do that. You can use
ReplaceAll (/.) with
rules for 1 and -1 to replace each number with an arbitrary image. This uses small blue up arrows and orange down arrows.
stateGraphics =
stateHistory /. {1 ->
Graphics[{Blue, Polygon@{{-1, 0}, {1, 0}, {0, 4}}},
ImageSize -> {15, 15}], -1 ->
Graphics[{Orange, Polygon@{{-1, 0}, {1, 0}, {0, -4}}},
ImageSize -> {15, 15}]}
Then we can go to each row and
Prepend a step number in front of it and then display the whole thing as a GraphicsGrid.
GraphicsGrid@
MapIndexed[
Prepend[#, Graphics[Text@First@#2, ImageSize -> {15, 15}]] &,
stateGraphics]
Here is all of the code as one expression. You can triple-click on different parts to select the various subexpressions when reading it in a notebook.
GraphicsGrid@
MapIndexed[
Prepend[#, Graphics[Text@First@#2, ImageSize -> {15, 15}]] &,
NestWhileList[
If[Total@#2 > Total@#, #2, #] & @@ {#,
MapAt[-# &, #, RandomInteger@10]} &, RandomChoice[{-1, 1}, 10],
Total@# < 10 &] /. {1 ->
Graphics[{Blue, Polygon@{{-1, 0}, {1, 0}, {0, 4}}},
ImageSize -> {15, 15}], -1 ->
Graphics[{Orange, Polygon@{{-1, 0}, {1, 0}, {0, -4}}},
ImageSize -> {15, 15}]}]
