If 200 is a close approximation to
$\infty$, then Sum[k^(Cos[1/k] - 2), {k, 1, 200}] // N = 5.78299.
But if one plots the partial sum vs the number of terms, one sees the following:
t = Table[{n, Sum[k^(Cos[1/k] - 2), {k, 1, n}]}, {n, 1, 5000, 100}];
ListLogLinearPlot[Table[{n, Sum[k^(Cos[1/k] - 2), {k, 1, n}]}, {n, 1, 5000, 100}], PlotRange -> All]
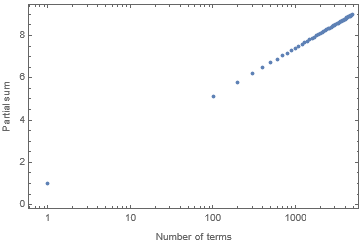
So I think you're correct in that the sum does not converge. But I don't know why Wolfram Alpha gives the answer it does.