@Alexander, first of all, this is a wonderful work, thank you very much for sharing! I gave a shout-out on LinkedIN and the feedback was great:

https://www.linkedin.com/feed/update/urn:li:activity:6866071848321368064

I am curious about stable fluid algorithm FDM you mentioned. Is there a general reference to it or it was developed in your report? I know NDSolve does use FDM

• https://reference.wolfram.com/language/tutorial/NDSolvePDE.html
• https://reference.wolfram.com/language/tutorial/NDSolveMethodOfLines.html

but I assume your FDM is a very custom thing.

I note that the code has multiple nest Do loops, and does not use NDSolve at all. I expect that there is a better way...

Also, the article does not reference Experimental Evidence of Hydrodynamic Instantons: The Universal Route to Rogue Waves, which is definitely relevant to this work.

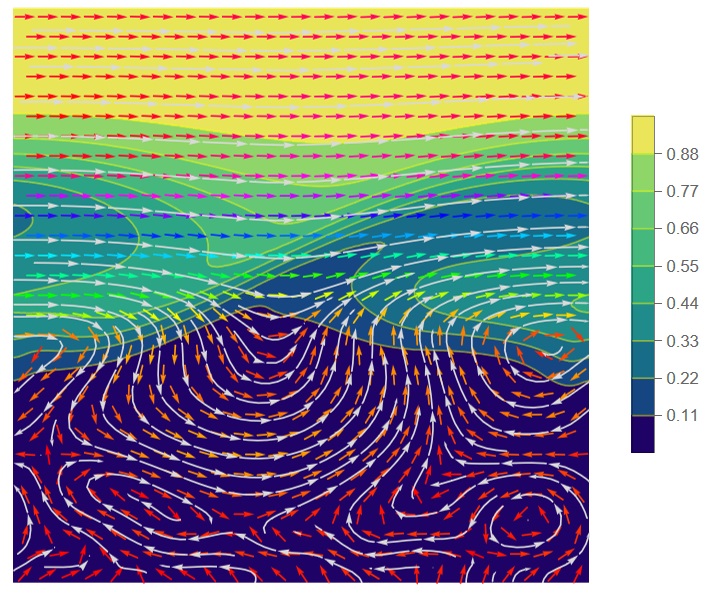
Next step is to animate wave transformation using interface function. We can show velocity field over density as follows

Show[ContourPlot[1 - rh[sm][x, y]/rhoWater20C, {x, 0, 1}, {y, 0, 1}, 
  PlotRange -> All, ColorFunction -> "BlueGreenYellow", Contours -> 8,
   ContourStyle -> Yellow, Frame -> False, PlotLegends -> Automatic], 
 StreamPlot[{Uvel[sm][x, y], Vvel[sm][x, y]}, {x, 0, 1}, {y, 0, 1}, 
  PlotRange -> All, StreamColorFunction -> None, VectorPoints -> Fine,
   VectorColorFunction -> Hue, PlotLegends -> Automatic, 
  StreamColorFunctionScaling -> True, StreamStyle -> LightGray]]

We can also compute frames for animation with using interface function

frames=Table[ContourPlot[1 - rh[i][x, y], {x, 0, 1}, {y, 0, 1}, 
  ColorFunction -> "BlueGreenYellow", Frame -> False, 
  PlotRange -> All, ImageSize -> Small, MaxRecursion -> 2, 
  Contours -> 8, ContourStyle -> Yellow, PlotLabel -> i], {i, 20, sm, 
  20}]; Animate[frames]