
In a previous thread and a previous demonstration we computed some basic facts about Trilobite and Crab tiling, but did not bother to prove aperiodicity. Even the original author admits that a full proof is "not worth the readers time" (https://arxiv.org/pdf/1608.07167.pdf). While this may be true assuming the proof is checked by a human, it may not be true with computational assistance. Here we argue that the computable proof is worth $10$ or $15$ minutes it takes to check (assuming the software isn't making unseen mistakes).
The strategy is simple: Given a representation of the tiling over five symbols--one blank crab, and one decorated trilobite in four rotations--first compute $2\times2$ and $3 \times 3$ atlases, and show that only $5$ of $49$ valid $3\times3$ templates are need to encompass the canonical completion obtained by adding $6$ tiles to each and every $2\times 2$ template. Canonical completions are so called because they are super-tiles of the five originals. Next we take and multiplex this set of $5$ into $5^9 \sim 2\times10^6$ possible super-super-tiles. After about $10$ minutes of computing, we need a little extra logic to prove closure of the atlas under inflation. This sets up an induction, which requires the chair hierarchy (modulo the known issue with fault lines).
Utility Functions
star = Join[IdentityMatrix[2], -IdentityMatrix[2]];
star2 = Plus @@ # & /@ Partition[star, 2, 1, 1];
ChairRep = {T[or_, 1] :> Join[{T[2 or, 1]},
MapThread[T[2 or + #1, #2] &, {star, Range[2, 5]}],
T[2 or + #, 1] & /@ star2],
T[or_, x_] :> Join[{T[2 or, x]}, MapThread[T[2 or + #1,
If[Or[#2 == x + 2, #2 == x - 2], x, #2]] &,
{star, RotateRight[Range[2, 5], 2]}],
T[2 or + #, 1] & /@ star2]};
InflateList[n_] :=
NestList[Union[Flatten[# /. ChairRep]] &, {T[{0, 0}, 1]}, n]
NeighborVals[data_, or_, verts_] :=
With[{verts2 = Map[Plus[or, #] &, verts]},
ReplaceAll[Cases[data, T[#, x_] :> x], {} -> {0}][[1]] & /@ verts2]
GetTemplates[data_, verts_] := Select[
NeighborVals[data, #[[1]], verts ] -> #[[2]] & /@
data, ! MemberQ[#[[1]], 0] &]
colRules = {1 -> Black, 0 -> White,
2 -> Hue[(2 - 1)/8], 3 -> Hue[(2 2 - 1)/8],
4 -> Lighter@Hue[(2 3 - 1)/8], 5 -> Lighter@Hue[(2 4 - 1)/8]};
Depict[v_, c_] := {c /. colRules, Rectangle[v]}
DepictTemplate[rule_, verts_] := Graphics[{
EdgeForm[Black], Depict[{0, 0}, rule[[2]]],
MapThread[Depict, {verts, rule[[1]]}]}]
Calculate Atlases
Using the substitution rule, we generate data and check to make sure we find all $2 \times2$ and $3 \times 3$ templates. In fact, once the $49$ larger templates are known, the $20$ smaller templates can be obtained by dissection.
Graphics[{EdgeForm[Black], InflateList[4][[-1]] /. T -> Depict}]

Length[ Union[GetTemplates[#, {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]]] & /@ InflateList[4]
templates = Union[GetTemplates[#, Join[star, star2]]] & /@ InflateList[4];
SortedInds = Cases[Position[templates[[-1]], #], {x_, 2} :> x] & /@ Range[1, 5];
Length /@ templates
Out[]= {0, 4, 20, 20, 20}
Out[]= {0, 1, 21, 49, 49}
(* These could prob. use more sorting *)
SortedTemplates = Function[{inds},
SortBy[templates[[-1, inds]], Reverse[#[[1]]] &]
] /@ SortedInds;
GraphicsGrid[
MapThread[#2[#1, Graphics[]] &, {Partition[
Show[DepictTemplate[#, Join[star, star2]], ImageSize -> 75
] & /@ Flatten[SortedTemplates], 7],
{Append, Prepend, Prepend, Append, Append, Append, Append}}]]

This data was obtained previously, but here we sort to emphasize five special templates in the first column, which also define inflations of the five basic symbols. These are most important templates to understand, but the remaining templates in the first three lines are also needed for reducing subsequent structured tuples. Before that, we also need $2 \times 2$ templates.
OnCenter = Cases[templates[[-1, All, 1]], {_, _, _, _, 1, 1, 1, 1}];
OffCenterB = Complement[templates[[-1, SortedInds[[1]], 1]], OnCenter];
OffCenterC = Complement[templates[[-1, All, 1]], Join[OnCenter, OffCenterB]];
TempToTiles[code_] := Prepend[
MapThread[T, {Join[star, star2], code}],
T[{0, 0}, code /. templates[[-1]]]]
CenterTiles = Sort[TempToTiles /@ OnCenter];
OffCenterBTiles = Sort[TempToTiles /@ OffCenterB];
OffCenterCTiles = Sort[TempToTiles /@ OffCenterC];
Atlas0 = Join[CenterTiles, OffCenterBTiles, OffCenterCTiles];
TwoAtlas0 = SortBy[Union[ Cases[#, T[{0, 0} | {1, 0} | {1, 1} | {0, 1}, _]
] & /@ Atlas0], Sort[#[[All, 2]]] &];
Length[TwoAtlas0]
Out[]=20
GraphicsGrid[ Transpose@ Partition[
Graphics[{EdgeForm[Thick], # /. T -> Depict}, ImageSize -> 100] & /@
TwoAtlas0, 4]]

A Few Case Checks
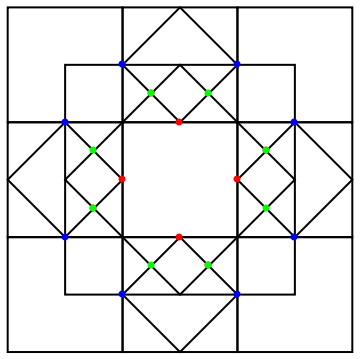
Although there are twenty $2 \times 2$ templates, up to rotation and reflection, only three are unique. We will now show how two of these three $2 \times 2$ templates are built uniquely into one of five special $3\times3$ templates. The remaining case is similar enough to leave as an exercise to the interested reader. Only one non-obvious lemma is needed: If two colored tiles have point-like adjacency, they must be related by a rotation of $\pm \pi/2$. Unfortunately, directionality is not obvious in this depiction, so we need to improve graphics before we can check anything.
The new directions are drawn on top of a grid,
Graphics[{Opacity[0], EdgeForm[Thick],
Polygon[star2], Polygon[star], Polygon[star2/2],
Function[{or}, Polygon[or + #/2 & /@ star2]] /@ star,
Function[{or}, Polygon[or + #/2 & /@ star2]] /@ star2,
Function[{or}, Polygon[or + #/2 & /@ star]] /@ star,
Opacity[1], PointSize -> Large, Red,
Point /@ (star/2), Point /@ (star/2 + star2/4),
Green, Point /@ (star/2 + star2/4),
Point /@ (star/2 + RotateRight[star2/4]),
Blue, Point /@ (star/2 + star2/2),
Point /@ (star/2 + RotateRight[star2/2])}]
DepictTC[or_, dir_] := {White, EdgeForm[Thick],
If[dir == 1, Darker@Gray, dir /. colRules],
Polygon[2 or + # & /@ Flatten[Transpose[
{star/2, star/2 + star2/4, star/2 + star2/4,
star/2 + star2/4 + RotateLeft[star2/2]}], 1]],
Gray, Polygon[2 or + # & /@ #] & /@ Transpose[{star/2 + star2/4,
star/2 + star2/2, star2,
star/2 + star2/2 + RotateLeft[star2/2],
star/2 + star2/4 + RotateLeft[star2/2]}],
If[dir == 1, {}, Transpose[{Part[RotateRight[{2, 3, 4, 5}, 2],
Complement[ Range[4], {RotateLeft[{1, 2, 3, 4}, dir - 2][[1]]}]] /. colRules,
Function[{or2}, Polygon[2 or + or2 + #/2 & /@ star]] /@ star[[
Complement[ Range[4], {RotateLeft[{1, 2, 3, 4}, dir - 2][[1]]}]
]]}]]}
GraphicsRow[ Graphics[DepictTC[{0, 0}, #], PlotRange -> {{-2, 2}, {-2, 2}},
ImageSize -> 100] & /@ Range[5]]

Now it is more obvious that rotation by $\pi/2$ acts as permutation of colors. According to bumps and nicks, we also have made join rules slightly more obvious. For example, black can not join black. Also note that colors here do not really matter, because tiles have fixed orientations. Our five target images are then depicted as
GraphicsGrid[{
Graphics[{EdgeForm[Thick], # /. T -> Depict}, ImageSize -> 150,
PlotRange -> {{-2, 2} + {1/2, 1/2}, {-2, 2} + {1/2, 1/2}}] & /@ CenterTiles,
Graphics[{EdgeForm[Thick], # /. T -> DepictTC}, ImageSize -> 150,
PlotRange -> {2 {-2, 2}, 2 {-2, 2}}] & /@ CenterTiles}]

And three characteristic pre-images are
GraphicsGrid[{
Graphics[{EdgeForm[Thick], # /. T -> Depict}, ImageSize -> 150,
PlotRange -> {{-2, 2} + {1/2, 1/2}, {-2, 2} + {1/2, 1/2}}] & /@
TwoAtlas0[[{1, 5, 15}]],
Graphics[{EdgeForm[Thick], # /. T -> DepictTC}, ImageSize -> 150,
PlotRange -> {2 {-2, 2}, 2 {-2, 2}}] & /@
TwoAtlas0[[{1, 5, 15}]]}]
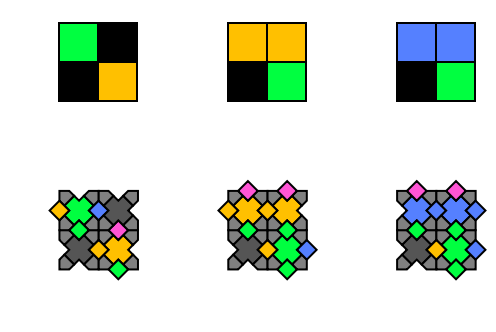
For the first case, we wrongly assume green neighbor to south, follow logical deductions, apply reflection symmetry, and finally complete with one extra black:
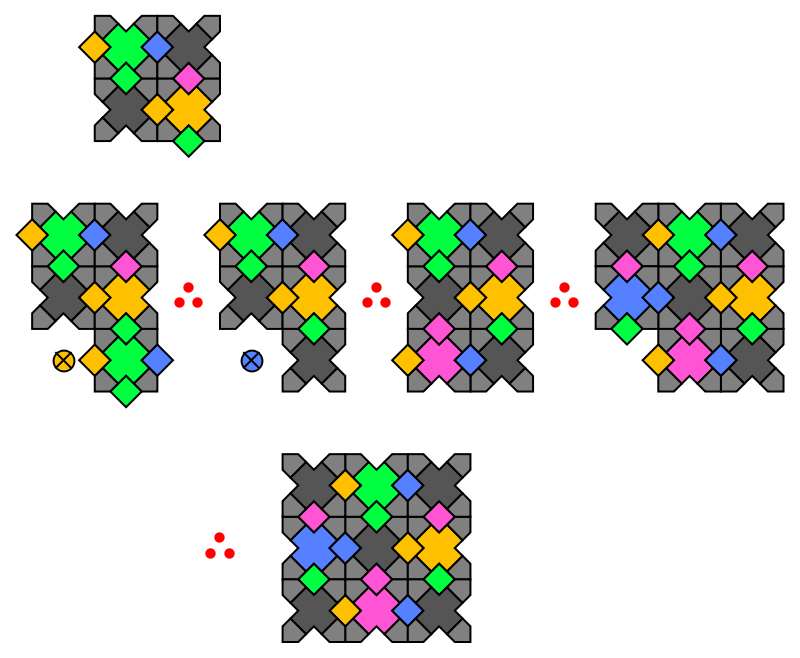
In this graphical shorthand notation, circle-x's indicate placements forbidden by the corner rule, while red circles stand for "therefore". The second case is slightly easier:
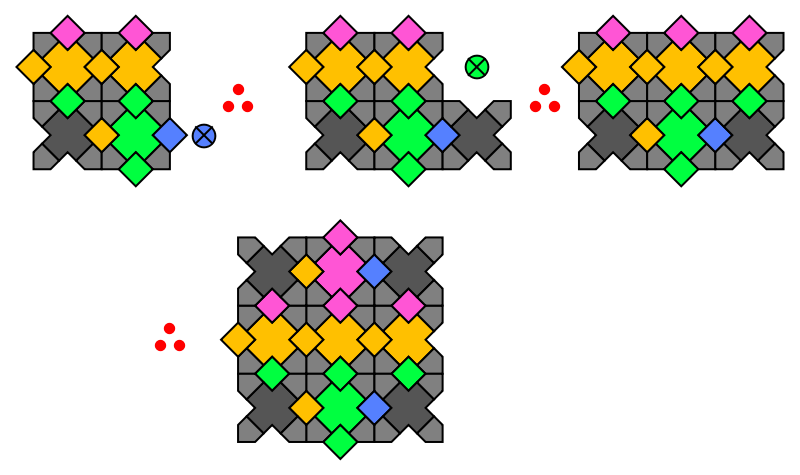
However, in the final completion we have ignored an equally valid pink-black-pink configuration for the top row. This is the notorious fault line issue, where it is legal to off-shift symmetry across an infinite line of trilobites, in this case yellow. To prove that fault lines must be infinitely long, we need one an alternating induction with two clauses:
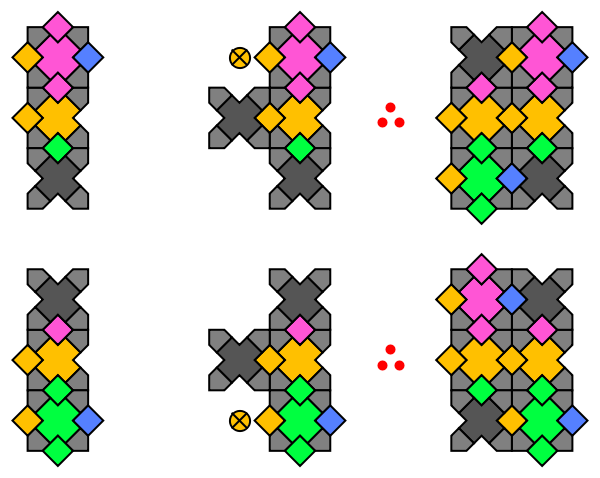
Thus to maintain asymmetry, the yellow line must extend indefinitely to the left. The third omitted case has a similar nuance, as should now be obvious. Logic for other seventeen cases can be written programmatically by applying symmetry transforms.
To recap: If the $2 \times 2$ template has two black tiles, it maps uniquely to the black supertile. If the $2 \times 2$ template has only one black, it maps uniquely to the supertile of whichever colored tile occurs twice. Because these unique completions exist, we can use the five special $3 \times 3$ templates as supertiles. Next we must prove that these supertiles close under inflation to $7 \times 7$ templates.
Edit: Nov. 9, 2:05 PM. Suggestion that the following code (could be expanded on) also proves unique completion:
TwoAtlasInds = Map[Position[Outer[Length@Intersection[#1, #2] &,
TwoAtlas0 /. T[x_, y_] :> T[x - #, y], CenterTiles, 1], 4] &,
{{0, 0}, {0, 1}, {1, 1}, {1, 0}}];
Length /@ TwoAtlasInds
Complement[Flatten[TwoAtlasInds[[All, All, 1]]], Range[20]]
TwoAtlasInds[[All, All, 2]]
Out[]= {5, 5, 5, 5}
Out[]= {}
Out[]= {{1, 2, 3, 4, 5}, {1, 2, 3, 4, 5}, {1, 2, 3, 5, 4}, {1, 2, 3,5, 4}}
Closure of Atlas under Inflation
Almost all the thinking is done, we now less than ten minutes of compute time on a personal lap top computer. This time is used to first check $(3 \times 3)^2 $ tiles overlap correctly, reducing to $ 3^4 - 4 \times 7 - 4 = 49$ unique tiles in each non-conflicted $7 \times 7$ template. Additional checks must be performed at four black vertices where four $3\times3$ templates meet at a corner, then we obtain a relatively small set of only $71$ templates.
ThreeByThree[code_, len_] := Union[Flatten[
MapThread[
CenterTiles[[#2]] /. T[or_, dir_] :> T[or + len #1, dir] &,
{Prepend[Join[star, star2], {0, 0}], code}]]]
(* about 7 minutes *)
AbsoluteTiming[CodesFirstPass = Select[Tuples[Range[5], 9],
SameQ[Length@ThreeByThree[#, 2], 49] &];][[1]]/60
filter[codes_, offset_, CheckTiles_, diff_] := Select[codes,
Function[{code}, SameQ[Min[Length[ Complement[
ThreeByThree[code, 2] /.
T[or_, dir_] :> T[or + offset, dir], #]
] & /@ CheckTiles], 49 - diff]][#] &];
CodesSecondPass =
FoldList[filter[#1, #2, OffCenterBTiles, 9] &, CodesFirstPass,
Tuples[{1, -1}, 2]];
Length /@ CodesSecondPass
Out[]={339, 201, 133, 87, 71}
SortedSecondPass = Function[{int},
Select[CodesSecondPass[[-1]], Count[#[[-4 ;; -1]], 1] == int &]] /@
Reverse[Range[0, 4]];
Length /@ SortedSecondPass
Function[{int}, Length@Select[templates[[-1, All, 1]],
Count[#[[-4 ;; -1]], 1] == int &]] /@ Reverse[Range[0, 4]]
diffs = %% - %
Total[%]
Out[]={5, 0, 16, 24, 26}
Out[]={5, 0, 4, 16, 24}
Out[]={0, 0, 12, 8, 2}
Out[]=22
GraphicsGrid[{Graphics[{EdgeForm[Black],
ThreeByThree[#, 2] /. T -> Depict}, ImageSize -> 200] & /@
SortedSecondPass[[1]],
Graphics[{EdgeForm[Black], ThreeByThree[#, 2] /. T -> DepictTC},
ImageSize -> 200] & /@ SortedSecondPass[[1]]}]

We are very happy to find these exact $5$ super-super-tiles, and can complete closure by proving the remaining 22 cases are spurious. Fourteen are eliminated by extension of the corner matching rule, and eight more are ignored as valid but faulty. Examples of the two classes are given as:
dCodes = Select[CodesSecondPass[[-1]], !
MemberQ[templates[[-1]], #[[2 ;; -1]] -> #[[1]]] & ];
Complement[#[[2 ;; -1]] -> #[[1]] & /@
Complement[CodesSecondPass[[-1]], dCodes], templates[[-1]]]
Length[dCodes]
SignalError = Join[
{1, _, _, _, _, #, _, #, _} & /@ Range[2, 5],
{1, _, _, _, _, _, #, _, #} & /@ Range[2, 5],
MapThread[{1, _, _, _, _, _, #1, _, #2} &, {
Range[2, 5], RotateRight[Range[2, 5], 2]}],
MapThread[{1, _, _, _, _, #1, _, #2, _} &, {
Range[2, 5], RotateRight[Range[2, 5], 2]}]]
dCodes2 = DeleteCases[dCodes, Alternatives @@ SignalError]
GraphicsRow[ Show[#, ImageSize ->
400] & /@ {Graphics[{ThreeByThree[dCodes[[1]], 2] /.
T -> DepictTC,
Red, Thickness[0.01], Arrowheads[0.05], Arrow[{{0, 0}, {4, 4}}],
Arrow[{{0, 0}, -{4, 4}}]}],
Graphics[ThreeByThree[dCodes2[[1]], 2] /. T -> DepictTC]
}]
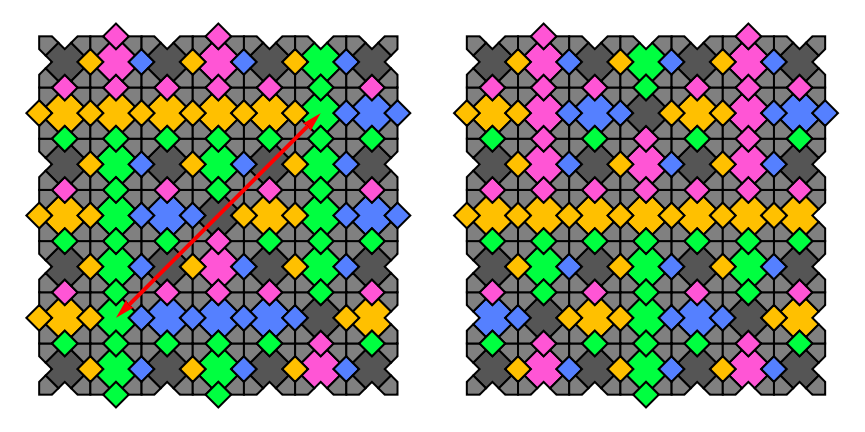
When the crab tiles are given orientations, matching signals propagate across the red axis, meeting at a conflict in on the central crab, thus invalidating the configuration. A really great idea is to program the trivial cellular automaton, which propagates crab directionality through the $7 \times 7$ super-super-tile, arriving at a conflict after only two time steps. For now we are happy with inspection, and invite the reader to look through all $22$ exceptions if necessary.
The Induction
Not much is left to be said. Since the first two atlases are identical up to scale, we have checked the base case of an induction which proceeds to say that successively larger $n^{th}$ order supertiles are proven combinatorially equivalent to the basic set of five symbols. At each step of the iteration, this requires orienting on black corners from the $(n-1)^{th}$ atlas to obtain a special set of only $5$ from the total set of $49$ . This process reveals the hierarchical symmetry and limit-periodicity of the five-color pattern. $\square$