Group Abstract Group Abstract

Message Boards Message Boards

Note on NKS ch.5 sec.7: Systems Based on Constraints

Brad Klee
Posted 4 years ago
POSTED BY: Brad Klee
3 Replies
Sort By:
Brad Klee
Brad Klee
Posted 4 years ago

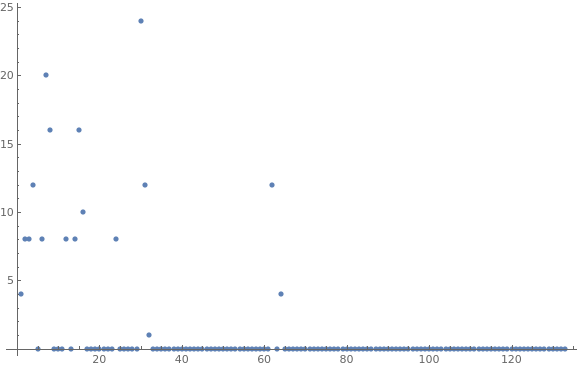
After g.t. $20$ minutes, the computer finally produced the following graph, which counts new rules needed as a function of time: 

Length /@ ReducedCodeData2
Total[%]
ListPlot[%%]

Out[]= {4, 8, 8, 12, 0, 8, 20, 16, 0, 0, 0, 8, 0, 8, 16, 10, 0, 0, 0, 0, 0, 
0, 0, 8, 0, 0, 0, 0, 0, 24, 12, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 12, 0, 4, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}

Out[]=179

chair rule count

When running the C.A. a small time savings (l.t. factor 2) can be found by using only the 179 rules. For reference those 179 rules are printed off as: 

AllRules2

Out[156]=

 {
{0, 0, 0, 1, 0, 0, 0, 0} -> 3
{0, 0, 0, 3, 0, 0, 0, 0} -> 3
{0, 0, 0, 5, 0, 0, 0, 0} -> 5
{0, 0, 0, 5, 0, 0, 0, 1} -> 5
{0, 0, 0, 5, 0, 0, 1, 0} -> 5
{0, 0, 0, 5, 0, 1, 0, 0} -> 5
{0, 0, 0, 5, 0, 1, 0, 1} -> 5
{0, 0, 0, 5, 0, 1, 1, 0} -> 5
{0, 0, 0, 5, 1, 0, 0, 0} -> 5
{0, 0, 0, 5, 1, 0, 0, 1} -> 5
{0, 0, 0, 5, 1, 0, 1, 0} -> 5
{0, 0, 0, 5, 1, 1, 0, 0} -> 5
{0, 0, 0, 5, 1, 1, 0, 1} -> 5
{0, 0, 0, 5, 1, 1, 1, 0} -> 5
{0, 0, 1, 0, 0, 0, 0, 0} -> 2
{0, 0, 1, 2, 0, 0, 2, 0} -> 5
{0, 0, 1, 4, 0, 0, 4, 0} -> 5
{0, 0, 2, 0, 0, 0, 0, 0} -> 2
{0, 0, 3, 1, 0, 0, 3, 0} -> 4
{0, 0, 3, 2, 0, 0, 1, 0} -> 1
{0, 0, 3, 4, 0, 0, 3, 0} -> 1
{0, 0, 4, 0, 0, 0, 0, 0} -> 4
{0, 0, 4, 0, 0, 0, 0, 1} -> 4
{0, 0, 4, 0, 0, 0, 1, 0} -> 4
{0, 0, 4, 0, 0, 0, 1, 1} -> 4
{0, 0, 4, 0, 0, 1, 0, 0} -> 4
{0, 0, 4, 0, 0, 1, 0, 1} -> 4
{0, 0, 4, 0, 1, 0, 0, 0} -> 4
{0, 0, 4, 0, 1, 0, 0, 1} -> 4
{0, 0, 4, 0, 1, 0, 1, 0} -> 4
{0, 0, 4, 0, 1, 0, 1, 1} -> 4
{0, 0, 4, 0, 1, 1, 0, 0} -> 4
{0, 0, 4, 0, 1, 1, 0, 1} -> 4
{0, 0, 4, 5, 0, 0, 0, 0} -> 1
{0, 0, 4, 5, 0, 0, 1, 0} -> 1
{0, 0, 5, 1, 0, 0, 5, 0} -> 4
{0, 0, 5, 2, 0, 0, 2, 0} -> 1
{0, 0, 5, 4, 0, 0, 4, 0} -> 1
{0, 0, 5, 4, 0, 0, 4, 1} -> 1
{0, 0, 5, 4, 0, 0, 5, 0} -> 1
{0, 0, 5, 4, 0, 0, 5, 1} -> 1
{0, 0, 5, 4, 0, 1, 4, 0} -> 1
{0, 0, 5, 4, 0, 1, 5, 0} -> 1
{0, 0, 5, 4, 1, 0, 4, 0} -> 1
{0, 0, 5, 4, 1, 0, 5, 0} -> 1
{0, 1, 0, 0, 0, 0, 0, 0} -> 5
{0, 1, 1, 4, 0, 4, 4, 0} -> 5
{0, 1, 1, 5, 0, 4, 0, 0} -> 5
{0, 1, 3, 0, 0, 3, 0, 0} -> 4
{0, 1, 5, 0, 0, 5, 0, 0} -> 4
{0, 2, 1, 0, 0, 2, 0, 0} -> 3
{0, 2, 3, 0, 0, 2, 0, 0} -> 1
{0, 2, 5, 0, 0, 1, 0, 0} -> 1
{0, 3, 0, 0, 0, 0, 0, 0} -> 3
{0, 3, 0, 0, 0, 0, 0, 1} -> 3
{0, 3, 0, 0, 0, 0, 1, 0} -> 3
{0, 3, 0, 0, 0, 0, 1, 1} -> 3
{0, 3, 0, 0, 0, 1, 0, 0} -> 3
{0, 3, 0, 0, 0, 1, 0, 1} -> 3
{0, 3, 0, 0, 0, 1, 1, 0} -> 3
{0, 3, 0, 0, 0, 1, 1, 1} -> 3
{0, 3, 0, 0, 1, 0, 0, 0} -> 3
{0, 3, 0, 0, 1, 0, 0, 1} -> 3
{0, 3, 0, 0, 1, 0, 1, 0} -> 3
{0, 3, 0, 0, 1, 0, 1, 1} -> 3
{0, 3, 1, 1, 0, 0, 4, 0} -> 3
{0, 3, 4, 0, 0, 0, 0, 0} -> 1
{0, 3, 4, 0, 0, 1, 0, 0} -> 1
{0, 4, 1, 0, 0, 4, 0, 0} -> 3
{0, 4, 1, 1, 0, 4, 4, 0} -> 3
{0, 4, 3, 0, 0, 3, 0, 0} -> 1
{0, 4, 3, 0, 0, 3, 0, 1} -> 1
{0, 4, 3, 0, 0, 3, 1, 0} -> 1
{0, 4, 3, 0, 0, 4, 0, 0} -> 1
{0, 4, 3, 0, 0, 4, 0, 1} -> 1
{0, 4, 3, 0, 0, 4, 1, 0} -> 1
{0, 4, 3, 0, 1, 3, 0, 0} -> 1
{0, 4, 3, 0, 1, 4, 0, 0} -> 1
{0, 4, 5, 0, 0, 5, 0, 0} -> 1
{0, 5, 0, 0, 0, 0, 0, 0} -> 5
{1, 0, 0, 0, 0, 0, 0, 0} -> 4
{1, 0, 0, 2, 0, 0, 0, 2} -> 5
{1, 0, 0, 4, 0, 0, 0, 4} -> 5
{1, 0, 4, 1, 0, 0, 0, 5} -> 4
{1, 0, 5, 1, 0, 0, 5, 5} -> 4
{1, 1, 0, 2, 2, 0, 0, 2} -> 5
{1, 1, 0, 5, 2, 0, 0, 0} -> 5
{1, 1, 1, 2, 0, 4, 0, 2} -> 5
{1, 1, 1, 2, 2, 4, 0, 2} -> 5
{1, 1, 1, 4, 2, 0, 4, 0} -> 5
{1, 1, 1, 4, 2, 4, 4, 0} -> 5
{1, 1, 1, 5, 2, 4, 0, 0} -> 5
{1, 1, 3, 0, 3, 3, 0, 0} -> 4
{1, 1, 3, 1, 0, 3, 0, 5} -> 4
{1, 1, 3, 1, 3, 3, 0, 5} -> 4
{1, 1, 4, 0, 3, 0, 0, 0} -> 4
{1, 1, 4, 1, 3, 0, 0, 5} -> 4
{1, 1, 5, 1, 3, 0, 5, 0} -> 4
{1, 1, 5, 1, 3, 0, 5, 5} -> 4
{1, 2, 0, 0, 2, 0, 0, 0} -> 3
{1, 2, 0, 1, 2, 0, 0, 2} -> 3
{1, 2, 1, 1, 2, 0, 4, 0} -> 3
{1, 2, 1, 1, 2, 0, 4, 2} -> 3
{1, 3, 0, 1, 0, 0, 0, 2} -> 3
{1, 3, 1, 1, 0, 0, 4, 2} -> 3
{1, 4, 0, 0, 4, 0, 0, 0} -> 3
{1, 4, 1, 1, 0, 4, 0, 2} -> 3
{1, 4, 1, 1, 0, 4, 4, 2} -> 3
{2, 0, 0, 0, 0, 0, 0, 0} -> 2
{2, 0, 0, 0, 0, 0, 0, 1} -> 2
{2, 0, 0, 0, 0, 0, 1, 0} -> 2
{2, 0, 0, 0, 0, 0, 1, 1} -> 2
{2, 0, 0, 0, 0, 1, 0, 0} -> 2
{2, 0, 0, 0, 0, 1, 0, 1} -> 2
{2, 0, 0, 0, 0, 1, 1, 0} -> 2
{2, 0, 0, 0, 0, 1, 1, 1} -> 2
{2, 0, 0, 0, 1, 0, 0, 0} -> 2
{2, 0, 0, 0, 1, 0, 1, 0} -> 2
{2, 0, 0, 0, 1, 1, 0, 0} -> 2
{2, 0, 0, 0, 1, 1, 1, 0} -> 2
{2, 0, 0, 5, 0, 0, 0, 0} -> 1
{2, 0, 0, 5, 0, 0, 0, 1} -> 1
{2, 0, 1, 1, 0, 0, 5, 0} -> 2
{2, 1, 1, 0, 0, 3, 0, 0} -> 2
{2, 1, 1, 1, 0, 3, 5, 0} -> 2
{2, 3, 0, 0, 0, 0, 0, 0} -> 1
{2, 3, 0, 0, 1, 0, 0, 0} -> 1
{2, 3, 4, 5, 0, 0, 0, 0} -> 1
{2, 3, 4, 5, 0, 1, 0, 1} -> 1
{2, 3, 4, 5, 1, 0, 1, 0} -> 1
{3, 0, 0, 1, 0, 0, 0, 3} -> 2
{3, 0, 0, 2, 0, 0, 0, 3} -> 1
{3, 0, 0, 4, 0, 0, 0, 1} -> 1
{3, 1, 0, 0, 3, 0, 0, 0} -> 2
{3, 1, 1, 0, 3, 3, 0, 0} -> 2
{3, 1, 1, 1, 3, 0, 5, 0} -> 2
{3, 1, 1, 1, 3, 3, 5, 0} -> 2
{3, 2, 0, 0, 2, 0, 0, 0} -> 1
{3, 2, 0, 0, 2, 0, 0, 1} -> 1
{3, 2, 0, 0, 2, 0, 1, 0} -> 1
{3, 2, 0, 0, 2, 1, 0, 0} -> 1
{3, 2, 0, 0, 3, 0, 0, 0} -> 1
{3, 2, 0, 0, 3, 0, 0, 1} -> 1
{3, 2, 0, 0, 3, 0, 1, 0} -> 1
{3, 2, 0, 0, 3, 1, 0, 0} -> 1
{3, 2, 5, 4, 2, 0, 5, 0} -> 1
{3, 2, 5, 4, 2, 0, 5, 1} -> 1
{3, 2, 5, 4, 2, 1, 5, 0} -> 1
{3, 2, 5, 4, 2, 1, 5, 1} -> 1
{3, 2, 5, 4, 3, 0, 4, 0} -> 1
{3, 2, 5, 4, 3, 0, 4, 1} -> 1
{3, 2, 5, 4, 3, 1, 4, 0} -> 1
{3, 2, 5, 4, 3, 1, 4, 1} -> 1
{3, 4, 0, 0, 4, 0, 0, 0} -> 1
{4, 0, 0, 0, 0, 0, 0, 0} -> 4
{5, 0, 0, 1, 0, 0, 0, 5} -> 2
{5, 0, 0, 2, 0, 0, 0, 2} -> 1
{5, 0, 0, 2, 0, 0, 0, 5} -> 1
{5, 0, 0, 2, 0, 0, 1, 2} -> 1
{5, 0, 0, 2, 0, 0, 1, 5} -> 1
{5, 0, 0, 2, 0, 1, 0, 2} -> 1
{5, 0, 0, 2, 0, 1, 0, 5} -> 1
{5, 0, 0, 2, 1, 0, 0, 2} -> 1
{5, 0, 0, 2, 1, 0, 0, 5} -> 1
{5, 0, 0, 4, 0, 0, 0, 4} -> 1
{5, 0, 1, 1, 0, 0, 5, 5} -> 2
{5, 1, 0, 0, 5, 0, 0, 0} -> 2
{5, 1, 1, 1, 0, 3, 0, 5} -> 2
{5, 1, 1, 1, 0, 3, 5, 5} -> 2
{5, 2, 0, 0, 5, 0, 0, 0} -> 1
{5, 4, 0, 0, 1, 0, 0, 0} -> 1
{5, 4, 3, 2, 0, 3, 0, 2} -> 1
{5, 4, 3, 2, 0, 3, 1, 2} -> 1
{5, 4, 3, 2, 0, 4, 0, 5} -> 1
{5, 4, 3, 2, 0, 4, 1, 5} -> 1
{5, 4, 3, 2, 1, 3, 0, 2} -> 1
{5, 4, 3, 2, 1, 3, 1, 2} -> 1
{5, 4, 3, 2, 1, 4, 0, 5} -> 1
{5, 4, 3, 2, 1, 4, 1, 5} -> 1
}

As indicated by the graph above, we strongly suspect these are the only rules need to infinity.

POSTED BY: Brad Klee
Brad Klee
Brad Klee
Posted 4 years ago

Chair Atlas

Chair Atlas

The following code uses the atlas above to derive a rule set for growing the chair tiling as a cellular automaton. As with Half Hex and Whole Hex examples, some extra rules are needed to kickstart growth. In this case we also need to do a little pruning of "obvious" rules. 

star = Join[IdentityMatrix[2], -IdentityMatrix[2]];
star2 = Plus @@ # & /@ Partition[star, 2, 1, 1];

ChairRep = {T[or_, 1] :> Join[{T[2 or, 1]},
     MapThread[T[2 or + #1, #2] &, {star, Range[2, 5]}],
     T[2 or + #, 1] & /@ star2],
   T[or_, x_] :> Join[{T[2 or, x]},
     MapThread[T[2 or + #1, If[Or[#2 == x + 2, #2 == x - 2], x, #2]] &,
      {star, RotateRight[Range[2, 5], 2]}],
     T[2 or + #, 1] & /@ star2]};

InflateList[n_] :=  NestList[Union[Flatten[# /. ChairRep]] &, {T[{0, 0}, 1]}, n]

NeighborLocs[or_] := Map[Plus[or, #] &, Join[star, star2]]

NeighborVals[data_, or_] := With[{verts = NeighborLocs[or]},
  ReplaceAll[Cases[data, T[#, x_] :> x], {} -> {0}][[1]] & /@ verts]

GetTemplates[data_] :=  Select[NeighborVals[data, #[[1]]] -> #[[2]] & /@ 
   data, ! MemberQ[#[[1]], 0] &]

templates = Union[GetTemplates[#]] & /@ InflateList[4];
Length /@ templates;

SortedInds = Cases[Position[templates[[-1]], #], {x_, 2} :> x] & /@ Range[1, 5];

partials[temp_] := ReplacePart[temp, Alternatives @@ # -> _] & /@ 
   Subsets[Range[Length[temp]]];

AllPartials = Union[Flatten[partials /@ templates[[-1, SortedInds[[#]], 1]], 
      1]] & /@ Range[5];

(*Only Grow From Colored vertices*)
exclude = Select[Flatten[AllPartials, 1], 
   Plus[Count[#[[1 ;; 4]], 2], Count[#[[1 ;; 4]], 3],
      Count[#[[1 ;; 4]], 4], Count[#[[1 ;; 4]], 5]] == 0 &];

FilteredPartials = Complement[AllPartials[[#]],
     Join[Flatten[AllPartials[[Complement[Range[5], {#}]]] , 1], 
      exclude] ] & /@ Range[5];

DefiniteRules = Map[Alternatives @@ FilteredPartials[[#]] -> # &, Range[5]];

StraightRulesB = Join[
   Map[Join[RotateRight[{0, 0, 0, 1}, # + 1], {0, 0, 0, 0}] -> # &, Range[2, 5]],
   Map[Join[ RotateRight[{0, 0, 0, #}, # + 1], 
          {1 | 0, 0 | 1, 0 | 1, 1 | 0}] -> # &, Range[2, 5]],
   Map[Join[ RotateRight[{0, #, 0, 0}, # + 1], {1 | 0, 0 | 1, 0 | 1, 
        1 | 0}] -> # &, Range[2, 5]] ];

AllRules = Join[StraightRulesB, DefiniteRules];

State0 = {Axiom[templates[[-1, -2]]], {}};

Iterate[state_] := With[{newVerts = Complement[
     Flatten[NeighborLocs[#] & /@ state[[1, All, 1]], 1],
     Flatten[state[[All, All, 1]], 1]]},
  Flatten /@ {MapThread[If[IntegerQ[#2], T[#1, #2], {}] &,
     {newVerts, ReplaceAll[NeighborVals[Flatten[state], #],
         AllRules] & /@ newVerts}], state}]

GrowList[n_] := NestList[Iterate, {{T[{0, 0}, 1]}, {}}, n]

Complement[InflateList[4][[-1]], Flatten[GrowList[2^(4 + 1)][[-1]]]]
Out[]={}

AbsoluteTiming[dat = Length /@ GrowList[2^6][[All, 1]]]
dat[[2 ;; -1]]/4
Flatten[Position[%, 3]]
Differences[%]

Out[]={1, 4, 8, 12, 16, 12, 20, 36, 36, 12, 20, 36, 44, 36, 60, 
  108, 84, 12, 20, 36, 44, 36, 60, 108, 100, 36, 60, 108, 132, 108, 
  180, 324, 204, 12, 20, 36, 44, 36, 60, 108, 100, 36, 60, 108, 132, 
  108, 180, 324, 236, 36, 60, 108, 132, 108, 180, 324, 300, 108, 180, 
  324, 396, 324, 540, 972, 516}

Out[]={1, 2, 3, 4, 3, 5, 9, 9, 3, 5, 9, 11, 9, 15, 27, 21, 3, 5, 9, 11, 9, 
15, 27, 25, 9, 15, 27, 33, 27, 45, 81, 51, 3, 5, 9, 11, 9, 15, 27, 
25, 9, 15, 27, 33, 27, 45, 81, 59, 9, 15, 27, 33, 27, 45, 81, 75, 27, 
45, 81, 99, 81, 135, 243, 129}

Out[]={3, 5, 9, 17, 33}

Out[]={2, 4, 8, 16}

As in the other cases, numeric outputs show log periodicity and Ulam Structure. Later we may also run some timing tests to see if we can speed up calculation of terms. For now we are happy with what we have.

POSTED BY: Brad Klee

enter image description here -- you have earned Featured Contributor Badge enter image description here Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!
POSTED BY: EDITORIAL BOARD