Hi Ahmed,
Thank you. I calculated the autocorrelation function for each list.
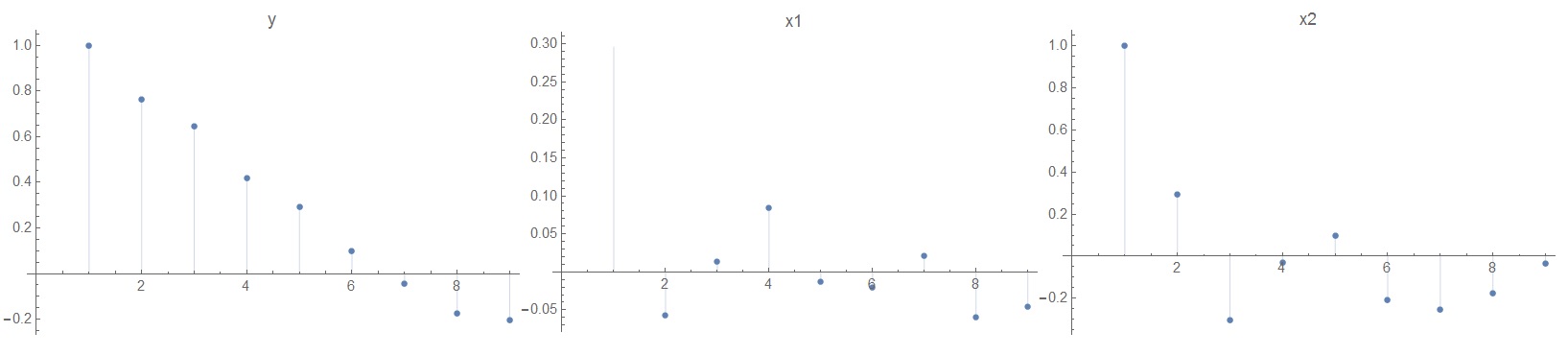
p1 = ListPlot[CorrelationFunction[y, {8}], Filling -> Axis,
PlotLabel -> "y"];
p2 = ListPlot[CorrelationFunction[x1, {8}], Filling -> Axis,
PlotLabel -> "x1"];
p3 = ListPlot[CorrelationFunction[x2, {8}], Filling -> Axis,
PlotLabel -> "x2"];
Style[Row[{p1, p2, p3}], ImageSizeMultipliers -> {1, ![enter image description here][1]1}]
I think I need a cross-correlation method. As you know, correlation is a linear measure of similarity between two signals. Cross-correlation is somewhat a generalization of the correlation measure as it takes into account the lag of one signal relative to the other. If lag == 0, then correlation = cross-correlation.Cross-correlation is particularly important to assess the causal relationship between two signals in time.
I did some things like the below:
In[10]:= temporalData = TemporalData[{Transpose[{y, x1}]}, Automatic];
In[11]:= correlations =
CorrelationFunction[temporalData, {-2, 2}]["Values"]
Out[11]= {{{0.647108, 0.436256}, {-0.0340549, 0.0141987}}, {{0.763739,
0.289174}, {-0.0396631, -0.0567463}}, {{1., 0.478399}, {0.478399,
1.}}, {{0.763739, -0.0396631}, {0.289174, -0.0567463}}, \
{{0.647108, -0.0340549}, {0.436256, 0.0141987}}}
I am not sure about this approach. Please note that we should have a function like this :
Y18= F [ x1 (at t=17), x1(at t=16),...x2(at t=17), x2(at t=16),...,Y17, Y16,Y15,... ]
Thank you so much again, Ahmed.