Silvia, you are probably right about that change in Version 12, according to the change log:

Major OS integration updates to Mac and Linux notebook interfaces using the 64-bit Cocoa API and Qt 5, respectively, with the Linux interface no longer requiring a supporting X server

Good, hope to move on from that error soon.

Your credentials appear impressive, so it looks like you could probably accept a challenge from my dissertation. If you want, see Fig. 2.13:

Is it possible to put in a camera (where projection to $\mathbb{R}^3$ is reasonably finite) that zooms around the surface, showing its features from different perspectives? I'm hoping for something like this:

obj = {Cos[#/50 Pi], Sin[#/50 Pi], 0} & /@ Range[110];
viewPt = 2 {1 + Sin[#/10 Pi], 0, Cos[#/10 Pi]} & /@ Range[20];
viewVec =   With[{tan = #[[3]] - #[[1]] & /@ 
      RotateRight[Partition[viewPt, 3, 1, 1]]},
   Divide[# - Cross[#, {0, 1, 0}] & /@ tan, 5]];

Graphics3D[{Blend[{Brown, Yellow}], Tube[obj, 1/2], Red, 
  MapThread[Arrow[{#1, #1 + #2}] &, {viewPt, viewVec}]},
 ViewVertical -> {0, 0, 1}, Boxed -> False, ViewPoint -> 3 {0, 1, 1}]

But the animation doesn't look anything like I would expect it to:

ListAnimate[Graphics3D[{Blend[{Brown, Yellow}], Tube[obj, 1/2]},
    ViewPoint -> viewPt[[#]], ViewVector -> viewVec[[#]],
    ViewAngle -> Pi/4] & /@ Range[20]]

There's plenty of vector space to play around with inventive angles, but the options so far are not very intuitive, agree with you.

Silvia's exploration is a common problem for all of us. The technical setting in details of Wolfram functions are always puzzles for users from old version to new version.

So, I dared not to rotate the camera; I usually rotate the object or model.

Hi Silvia, nice post. Thought to add a note, since I've been on this topic lately.

Usually setting ViewVertical & ViewPoint is enough to get a good result. ViewVertical defines a directed line in space, and ViewPoint a point (obviously). Looking from the point there is one rotational degree of freedom, which is then fixed to the vector of ViewVertical. Perspective can be controlled by taking near or far ViewPoints, with limit to infinity approaching ViewProjection->"Orthographic" (?). The problem is with bounding box. Using some of the previous chess assets:

glist1 = Show[GameState[TwoKnights], 
     Graphics3D[{Black, Sphere[{0, 0, 2}],
       Sphere[RotationMatrix[Pi/50 #, {0, 0, 1}].{0, 64, 0}] & /@ 
        Range[100]}],
     ViewPoint ->  100 ({Sqrt[2] Cos[Pi/50 *#], Sqrt[2] Sin[Pi/50 *#], 1}),
     Boxed -> True, ViewVertical -> {0, 0, 1}, 
     PlotRange -> {{-65, 65}, {-65, 65}, {-2, 16}},
     ImageSize -> 500] & /@ Range[0, 100];
ListAnimate[glist1]

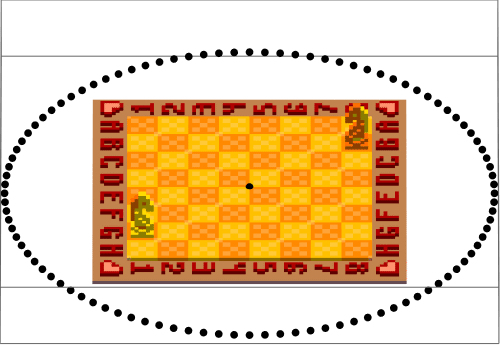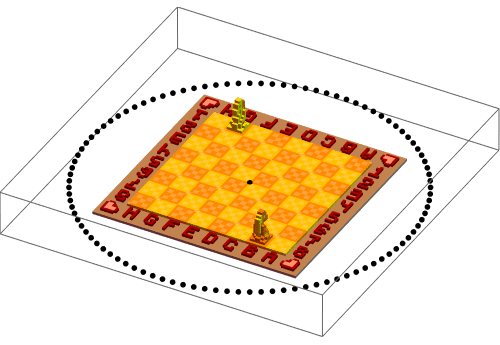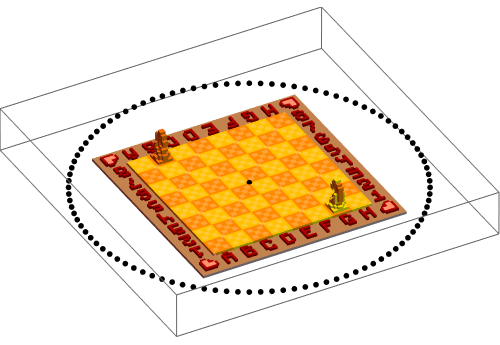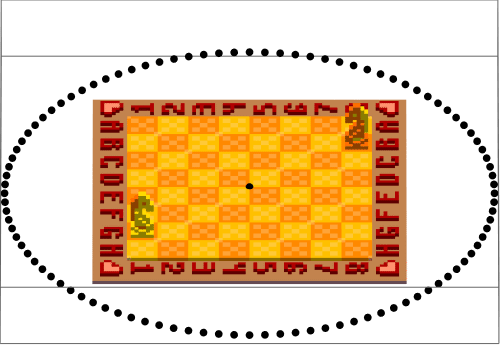
This is not what we want, and setting Boxed->False does not change much. According to stack exchange, there is another option to set "ShrinkWrap"?? Anyways, here's an improved rotation:

glist2 = Show[GameState[TwoKnights], 
     Graphics3D[{Black, Sphere[{0, 0, 2}],
       Sphere[RotationMatrix[Pi/50 #, {0, 0, 1}].{0, 64, 0}] & /@ 
        Range[100]}],
     Boxed -> False, Method -> {"ShrinkWrap" -> True},
     ViewPoint -> 100 ({Sqrt[2] Cos[Pi/50 *#], Sqrt[2] Sin[Pi/50 *#], 1}),
     ViewVertical -> {0, 0, 1}, 
     PlotRange -> {{-65, 65}, {-65, 65}, {-2, 16}},
     ImageSize -> 500] & /@ Range[0, 100];
ListAnimate[glist2]

This looks much better, though the animation still has a bit of jitter. If I were to mask out the black spheres on the boundary, probably it would look slightly more smooth.

-- you have earned Featured Contributor Badge Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!