This is a question directly related to several other previous questions of mine, however most directly related to Torn Equations
Besides that question, I have also (through Mathematica) modeled, simulated and controlled a flywheel inverted pendulum (youtube link)
This works well, and I have a good mathematical understanding of the model equations, which is why it, and the other previous testbench (as seen in my Torn equations question) are my direct comparisons to models I've made SystemModeler.
When improving my models using RotorWith3DEffects I realized that this particular class isn't quite used as exactly as the other Rotor and also isn't quite connected the same in order to achieve the 1DOF inertia on a 3D body. When reading the documentation there is a single line
Gyroscopic torques appear, if the vector of the carrier body's angular velocity is not parallel to the vector of the rotor's axis.
Which for my English is a bit cryptic, but fine. When looking at suggested other examples, such as GyroscopicEffects
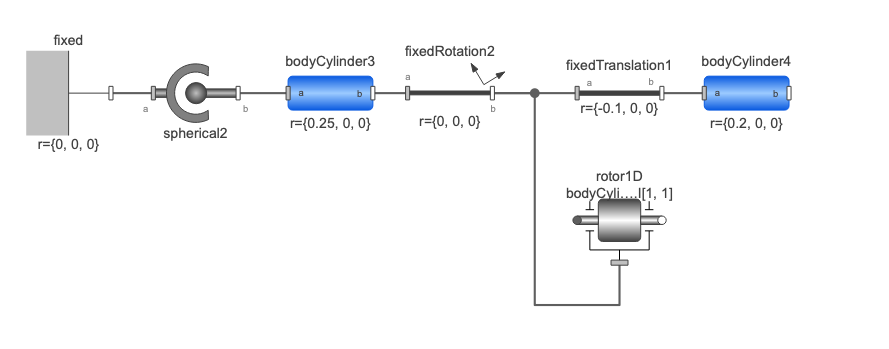
It shows that the class is connected via the Housing connector. So I do this as well in my models, which produce great results that match the real model and the Mathematica version.
My issue now comes that when trying to improve my BLDC motor model, which is a maxon EC45 Flat, an "aussen roller" Or namely a motor with rotating housing, clearly also has a rotating inertia that I want to include to complete my model.

Because I want to use this in a library/package later for reuse, I want to the motor model to be complete, and not simply add it's inertia to an outside class.
The problem here arises, when I want to connect the motor model shaft of the inner RotorWith3DEffects to an 'shaft' or outer RotorWith3DEffects the gyroscopic effects disappear.
But this is fine, clearly I have a misunderstanding. So I tried to experiment with 5 different modeling/connection techniques to figure out how to connect this model correctly.
Unfortunately, I now have 5 different results, none of which are similar, and only one that sort of resembles the model from Mathematica, except it appears to have energy being constantly added to the system, instead of it dissipating.
The Mathematica ODEs are :
Where $\alpha(t)$ is the pendulum angle, and $\phi(t)$ is the motor angle. with various inertias, friction and masses.
$$\left\{g \sin (\alpha (t)) (k \text{mw}+l \text{mb})+\text{jw} \phi ''(t)+\Theta \alpha ''(t)=-\text{rb} \alpha '(t)-\mu \tanh \left(\frac{\alpha '(t)}{\iota }\right),\text{jw} \left(\alpha ''(t)+\phi ''(t)\right)=\tau u(t)-\text{rw} \phi '(t)\right\}$$
When given a simple constant input of 0.6 at $u(t)$ from hanging position of initial angle $\alpha(0) = 0$ the Motor spins up, causes swinging and short lived constant offset before the system falls back to angle zero as seen here:
Also 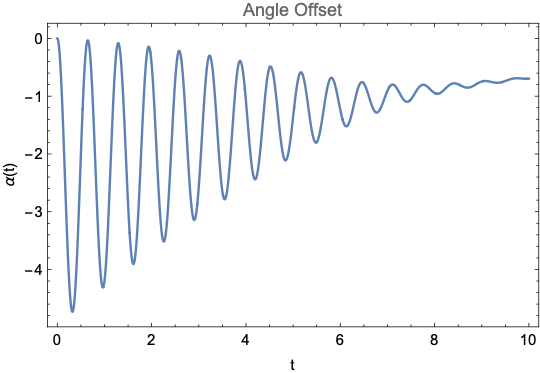
When using the actual physical model, this also happens, pretty much exactly the same, as such I am confident this is modeled fairly well.
As mentioned unfortunately, when doing this same within my 5 different experiments, I don't get any of the same results but instead either no displacement whatsoever, a constant non-dissipating oscillation or a constant angle accumulation that eventually breaks the simulation, as seen here:
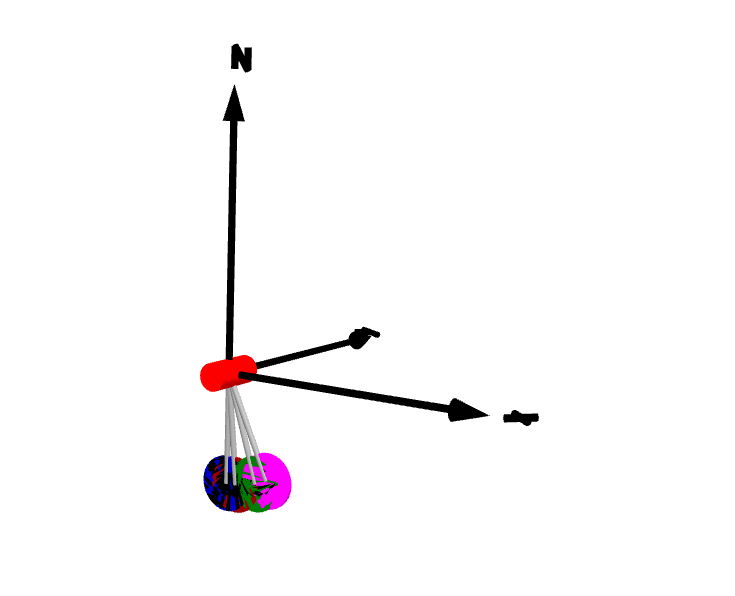
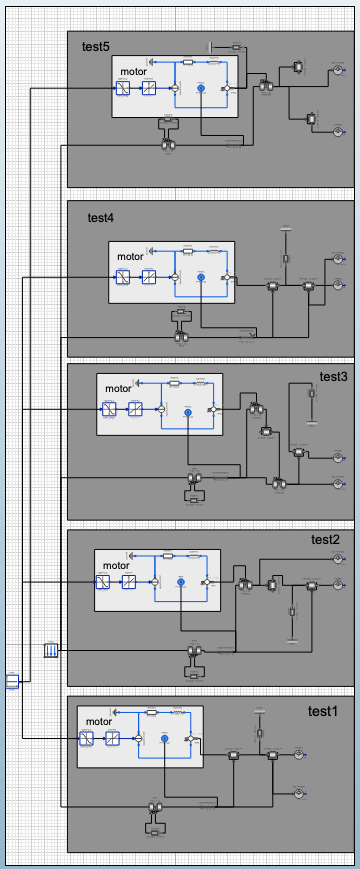
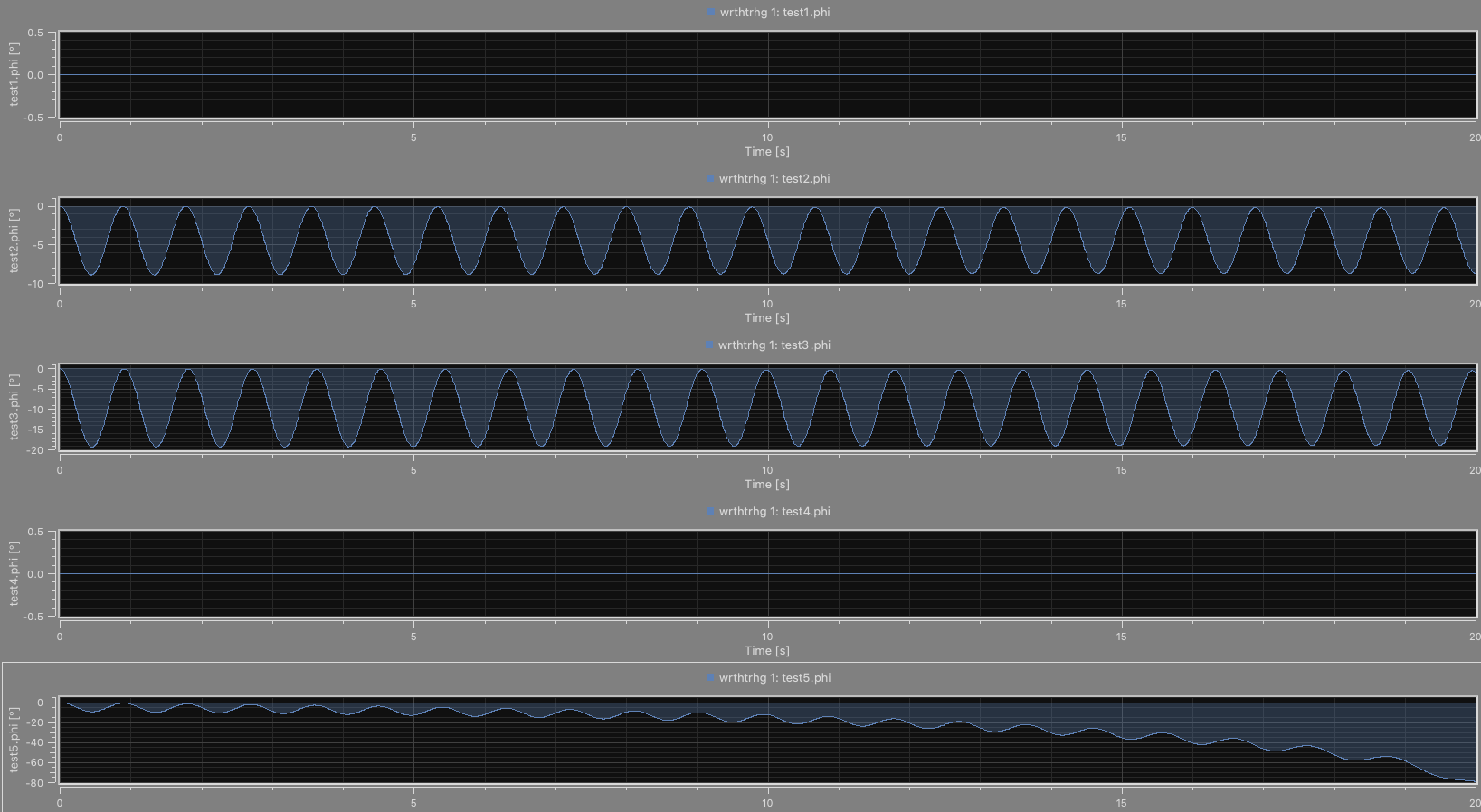
TLDR: I want to be able to use RotorWith3DEffects like Rotor to get gyroscopic effects with my internal motor model, and be able to use the rotors shafts as connection points, rather the housing, however it seems this isn't possible in the way I expect it, and when comparing different connect methods, against Mathematica, I get wildly different results, and I don't know which one is correct, and baring all of them are wrong, then I'm completely stuck.
How do I use this class correctly, the description and one single example within the documentation don't specify this enough for me, and the many test results don't match up with my real world model or Mathematicas.
I have included the Mathematica files and System modeler file within this post for your own testing, done in System modeler 12.3. Thanks for the help.
 Attachments:
Attachments: