How much code do you think you need to make this animation?
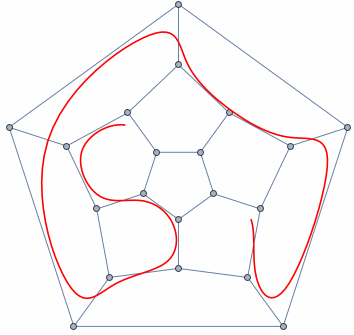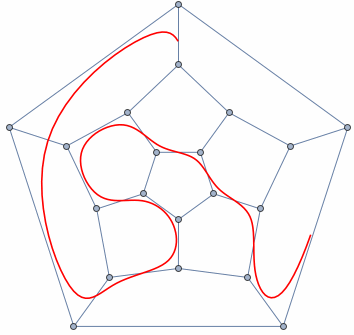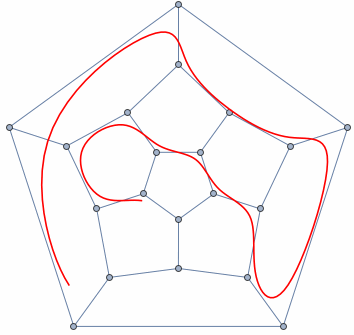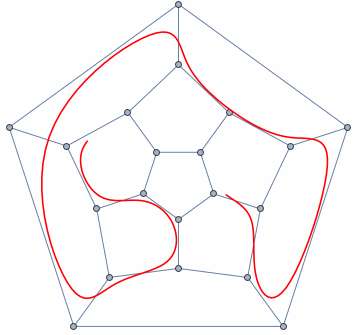
Not much:
Animate[
gg = PolyhedronData["Dodecahedron", "SkeletonGraph"];
ff = BSplineFunction[GraphEmbedding[gg][[FindHamiltonianCycle[gg][[1, All, 1]]]], SplineClosed -> True];
Dynamic@Show[gg, ParametricPlot[ff[t - s], {t, 0, .8}, PlotStyle -> Red]], {s, 0, 1}]
Let's see how these things work. Imagine you have a Graph structure to visualize. To be concrete, consider a Hamiltonian Cycle of a graph. And the goal is to visualize this cycle with an animation. Here is a simple approach for Dodecahedron whose SkeletonGraph is Hamiltonian:
g = PolyhedronData["Dodecahedron", "SkeletonGraph"];
c = FindHamiltonianCycle[g]
Out[] = {{1<->14,14<->9,9<->17,17<->19,19<->3,3<->7,7<->16,16<->8,8<->4,4<->20,20<->6,6<->12,12<->11,11<->5,5<->2,2<->13,13<->18,18<->10,10<->15,15<->1}}
HighlightGraph[g, PathGraph[First[%]]]
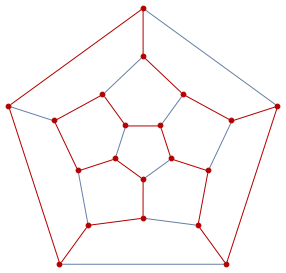
You can extract coordinates of vertices in the Hamiltonian Cycle and connect them by a spline:
Show[g, Graphics[{Red, Thick, BSplineCurve[GraphEmbedding[g][[c[[1, All, 1]]]]]}]]
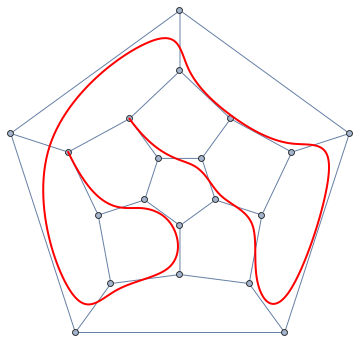
Or the same for a set of polyhedra:
Show[#, Graphics[{Red, Thick, BSplineCurve[GraphEmbedding[#][[FindHamiltonianCycle[#][[1, All, 1]]]]]}]] & /@
(PolyhedronData[#, "SkeletonGraph"] & /@ PolyhedronData["SkeletonGraph", "Defined"][[;; 16]])
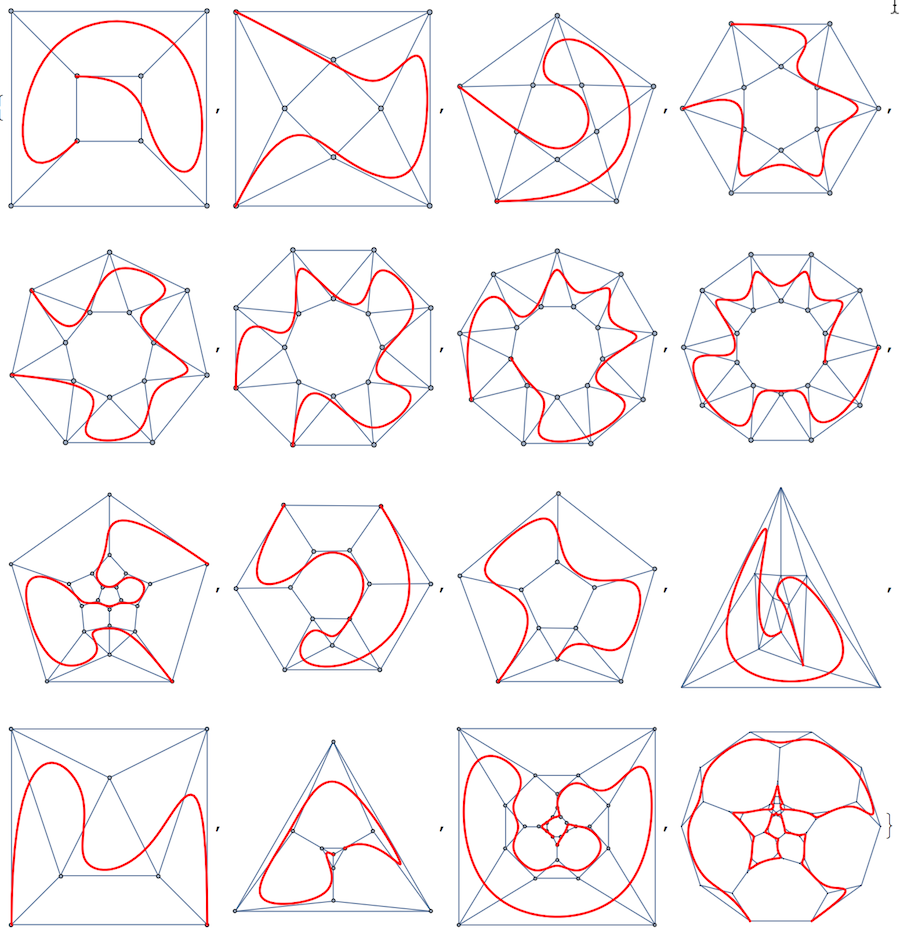
Repeating every vertex coordinate inside the spline twice will make the spline come close to the vertex. We can actually use BSplineFunction for animation:
bsf = BSplineFunction[Flatten[Transpose[Table[GraphEmbedding[g][[c[[1, All, 1]]]], {2}]],1], SplineClosed -> True];
Animate[Show[
g,
ParametricPlot[bsf[x], {x, 0, 1}, PlotStyle -> Directive[Blue, Opacity[.2], Thickness[.02]]],
Graphics[{{Brown, Opacity[.3], Thickness[.05], BSplineCurve[GraphEmbedding[g][[c[[1, All, 1]]]]]},
{Red, PointSize[.03], Point[bsf[t]]}}]
], {t, 0, 1, AnimationRate -> .1}]
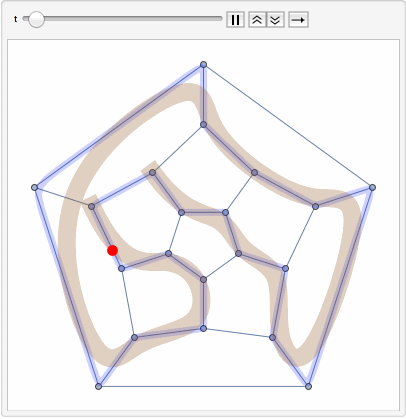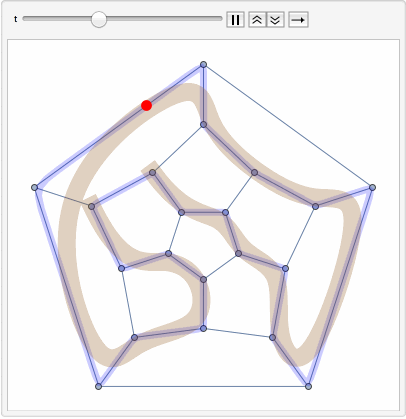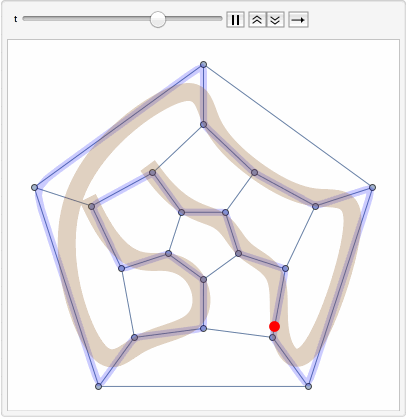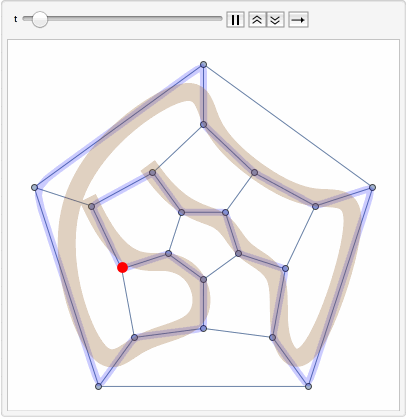
And the very first animation is very similar in nature. BUt instead of a point it runs the offset with which ParametricPlot starts plotting.