You know you're a developer when your various projects converge into one coherent whole, and that is when the code base begins to exceed the scope of one blog post. Here we will synthesize three dimensional generalization of the Autoglyphs with recent developments in practice of Chinese Trigram design. A complete working example is available on the cloud, so we will not repeat all code here. Yes, we are heading toward a coding competition for New Year Water Tiger 2022. First we need to give some background, prove a concept, and show how basic encrypt / decrypt functions work. Raw voxel assets are available on github.
If you have already studied linear recurrences extensivley on OEIS, it probably is okay to skip Tanja's series on Feedback Shift Registers and get straight to Symmetric Crypto. Eventually we are going to try and decrypt a stream cipher (good luck), but for now we have to define Encrypt and Decrypt functions, which make the Autoglyphs more useful than mere works of art. The Autoglyphs are actually patterns and not entirely random outputs. We ask the question if pattern and symmetry allows the possibility that maybe some Eve can obtain decodes (without taking secret keys and brute forcing)?
Let's start with a simple import of $8$ pads, each a 3D Autoglyph (after sorting by symmetry):
AGTests = Map[Partition[#, 64] &,
Partition[Flatten[Map[ToExpression, Characters /@ StringSplit[Import[
"https://raw.githubusercontent.com/bradklee/CryptoAssets/master/ExampleAG3Ds/AG3DT"<>ToString[#]<>".txt"],"\n"]]], 64*64]] & /@ Range[8];
These pads are definitely not secure, because the corresponding secret keys are already known and listed online:
CharacteristicSeeds = {
1068947993658975122157353753616942840246806141024,
875695379343193424823445348694680652740201185481,
495672220319428784155078550997997180172599139322,
92962701827533250346487117218119002306342033068,
807669444641696051849891548387372924883122769942,
58854672879382211919039871200182349957445942893,
207752697509440412973534330689716944749507327427,
751209551927174784144601640564624173088665128391};
Mod[Floor[{#, #/2, #/4}], 2] & /@ CharacteristicSeeds;
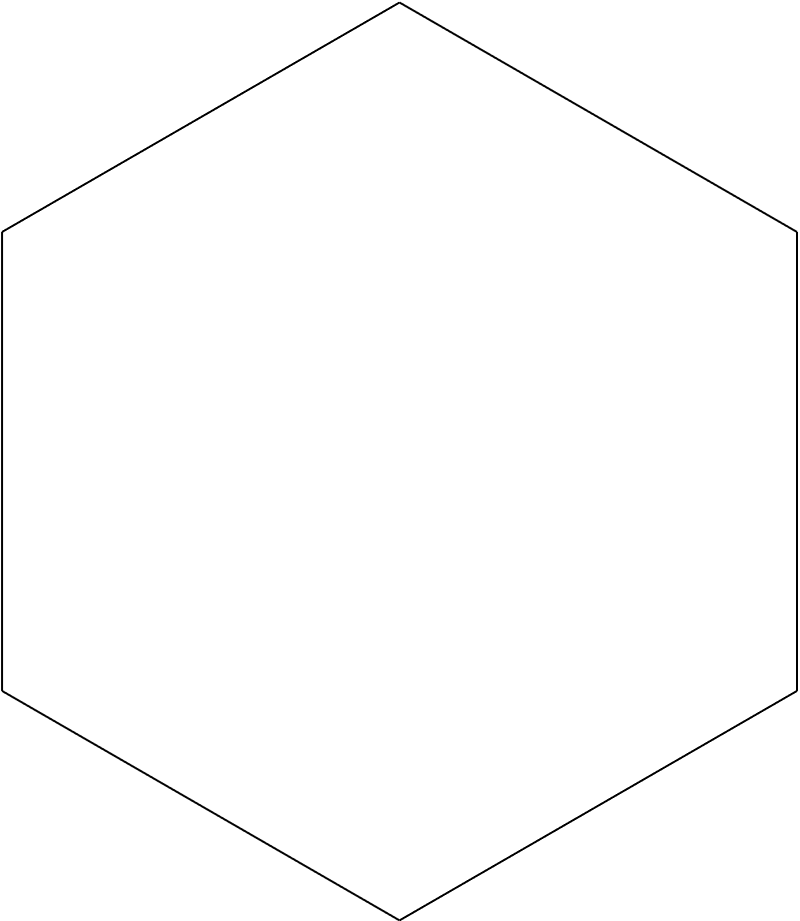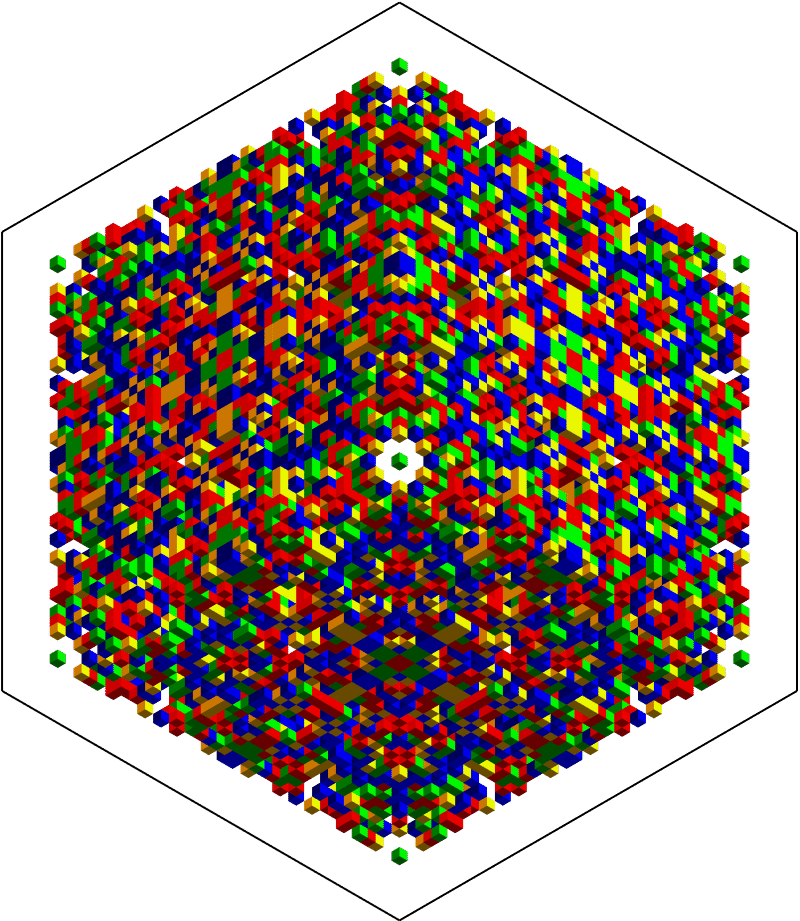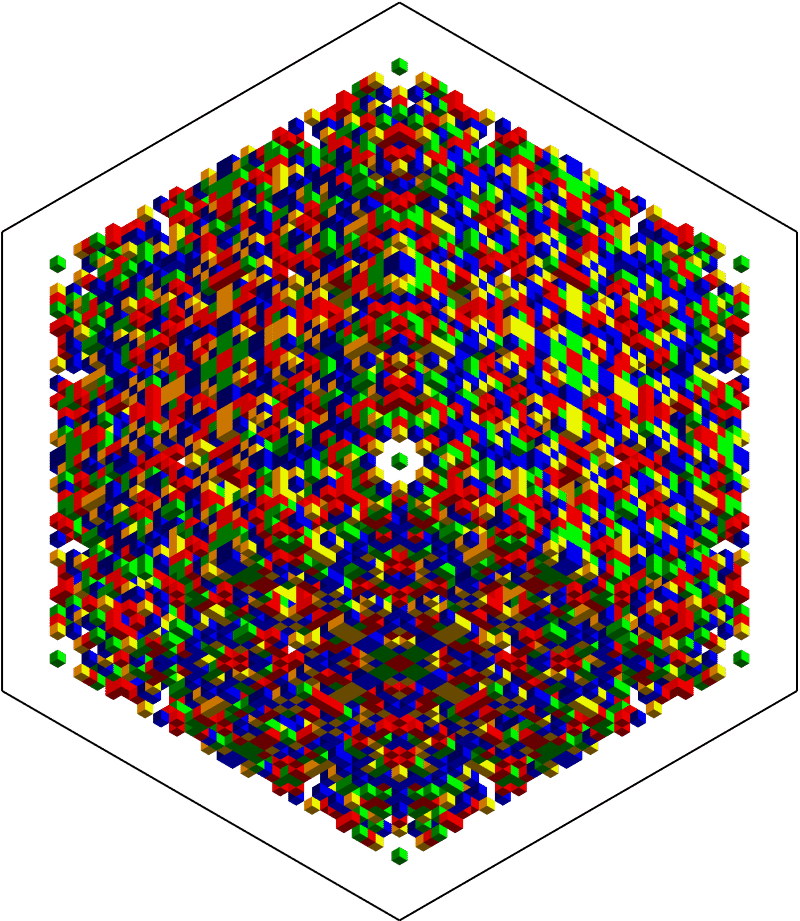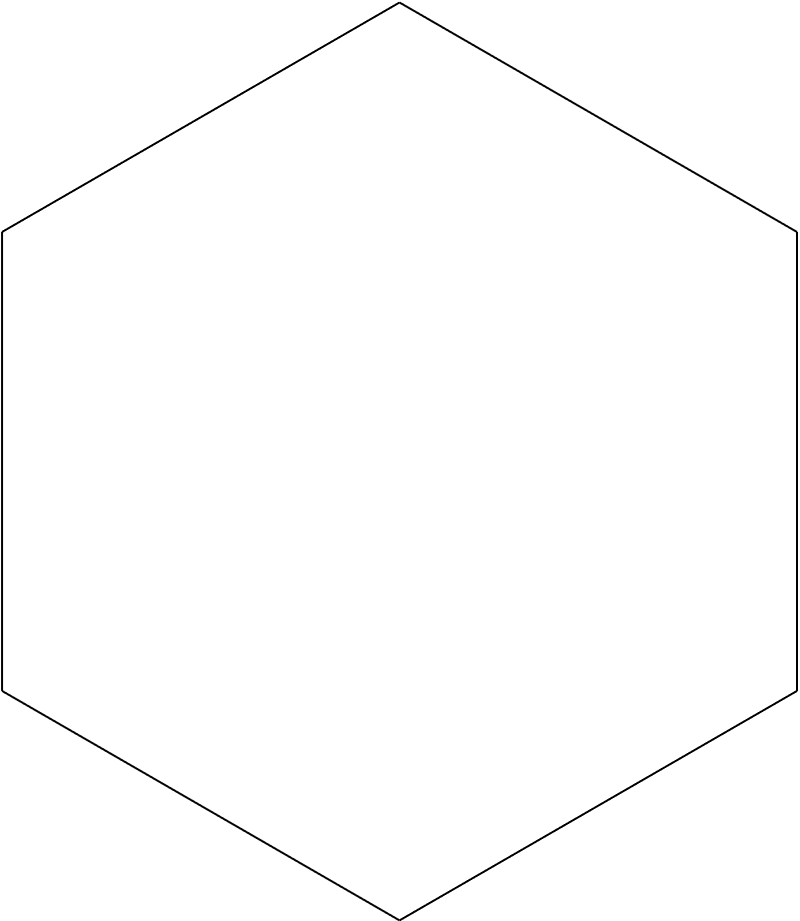
One of the chosen AGs has full Octahedral symmetry:
Show[Trigram@AGTests[[-1]], ImageSize -> 600]

Nothing hidden inside so far, but it's difficult to tell. The main question to ask is whether or not the pattern is stochastic enough to make an effective mask for potentially sensitive information? Maybe not, in which case some intrepid crypto cracker could actually win the subsequent contest while playing fair. Other than overall symmetry, notice that $32 \times 32 \times 32$ blocks on each corner have transpose symmetry on each facet. This is an important property when understanding the minimal encoding. An example follows.
Now we get the first example data set, and depict one of the encryptions:
data = Map[Partition[#, 32] &, Partition[Flatten[
Map[ToExpression, Characters /@ StringSplit[ Import[
"https://raw.githubusercontent.com/bradklee/CryptoAssets/master/ExCrypt1/CryptogramT"
<>ToString[#] <> ".txt"],
"\n"]]], 32*32]] & /@ Range[24];
Trigram@data[[1]]

For minimum encodings we only use one of eight corners from an AG to pad a $32 \times 32 \times 32$ signal. If you're following the discussion, you may be thinking why $32$ rather than $16$? We will get there, but first a brute force attack over length $8$ seed space:
TableForm[ Partition[Trigram@MinDecode[#, data[[1]]] & /@ CharacteristicSeeds, 4]]

So okay, we got lucky with a small key space and hit a decode on index $4$. I think the plots look cool, but some people would rather just read the numbers and save time:
Total[Flatten[MinDecode[#, data[[1]]]]] & /@ CharacteristicSeeds
{6639, 5980, 6815, 2441, 6490, 6101, 6739, 6689}
Due to sparseness of readable outputs, the weight of the decode is noticeably less than other fail cases, again index $4$. We can do similar for subsequent cryptograms and get the decrypt index map. Here we go with a few plots:
encryptions = data[[{1, 3, 6}]];
NotExactlySecretKeys = CharacteristicSeeds[[{4, 3, 7}]];
EncryptedTrigrams = Show[Trigram[#], ImageSize -> 200] & /@ encryptions;
decodes = MapThread[MinDecode, {NotExactlySecretKeys, encryptions}];
PublicEncrypted = CubeEncode /@ decodes;
RGBBWResults /@ PublicEncrypted[[1;;2]]
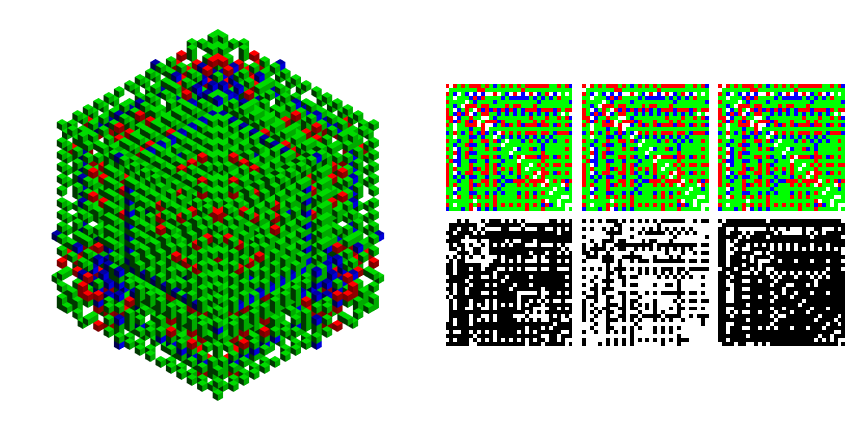
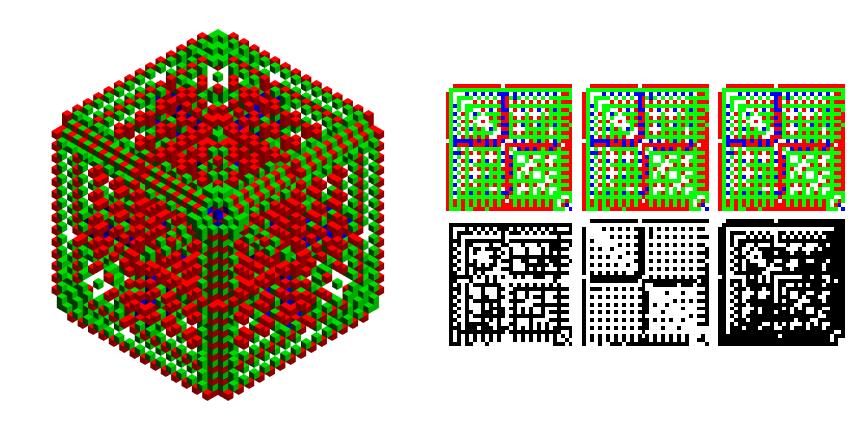
RGBBWResults /@ decodes[[1;;2]]
So what's going on with the intermediary result? In order to preserve transpose symmetry we need a permutation step from $16\times 16\times 16 \rightarrow 32\times 32\times 32 $. Essentially this is an extra, necessary encryption, with a public key:
(* Loc2Locs is invertible, thus a Permutation Public Key *)
Loc2Locs[loc_, 1] := 2 loc - # & /@ {{1, 1, 1}, {0, 0, 0}}
Loc2Locs[loc_, 3] := With[{oddPos = Position[loc,
Complement[loc, Commonest[loc]][[1]]][[1, 1]]},
SortBy[2 loc - # & /@ {
ReplacePart[Table[0, {i, 3}], oddPos -> 1],
ReplacePart[Table[1, {i, 3}], oddPos -> 0],
{0, 0, 0}}, Total[#] &]]
Loc2Locs[loc_, 6] := SortBy[2 loc - # & /@
Join[IdentityMatrix[3], 1 - IdentityMatrix[3]],
{Total[#], Sort[Permutations[#]][[1]]} &]
Once we get to $32\times 32\times 32 $, then to finish encryption, we just add the pad mod 5. We could actually have skipped the permutation layer by using a $16\times 16\times 16 $ pad, but the first example is just a means to the second. Here's another mixed-up dataset to get and try to straighten out:
SymCryptograms = Map[Partition[#, 64] &,
Partition[Flatten[Map[ToExpression, Characters /@ StringSplit[Import[
"https://raw.githubusercontent.com/bradklee/CryptoAssets/master/ExCrypt2/SymCryptogram"<>ToString[#]<>".txt"],"\n"]]], 64*64]] & /@ Range[8];
decsTest = SymDecode[SymCryptograms[[1]], #] & /@ AGTests;
Length /@ decsTest
Column[RGBBWResults /@ decsTest[[4]]]
Out[]={4, 4, 4, 2, 4, 4, 4, 2}
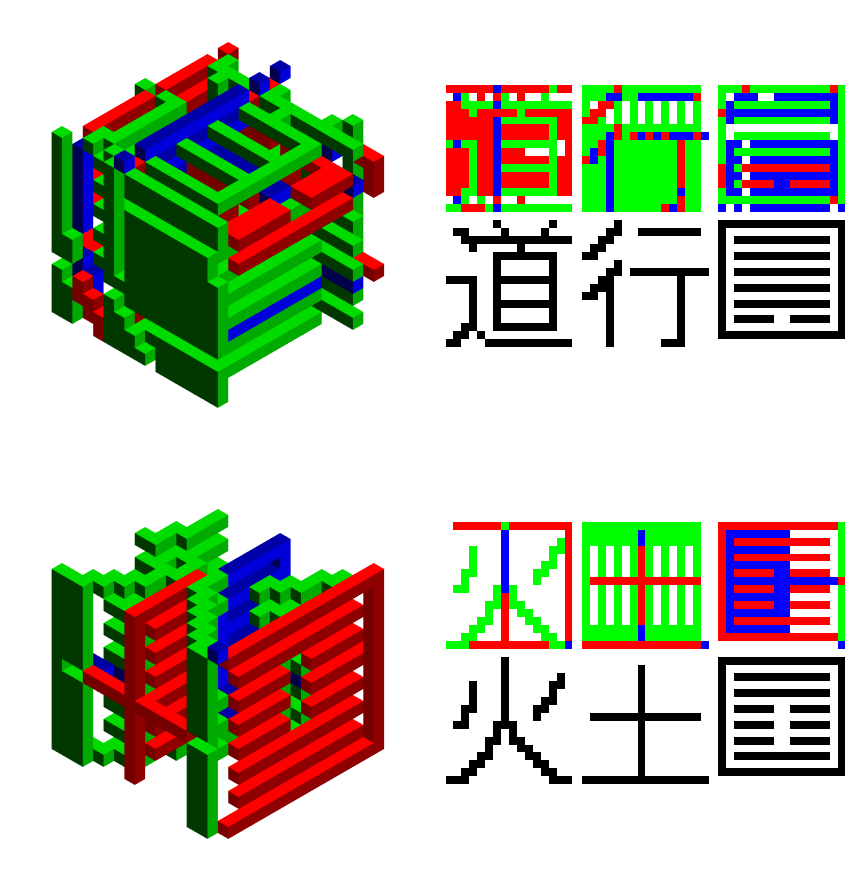
Basically, the fourth type of Autoglyph has $2\times D_2$ dihedral symmetry, so we were able to embed two characters rather one. The reason for not breaking symmetry is to keep up appearances the that encrypted file could actually still be an Autoglyph 3D:
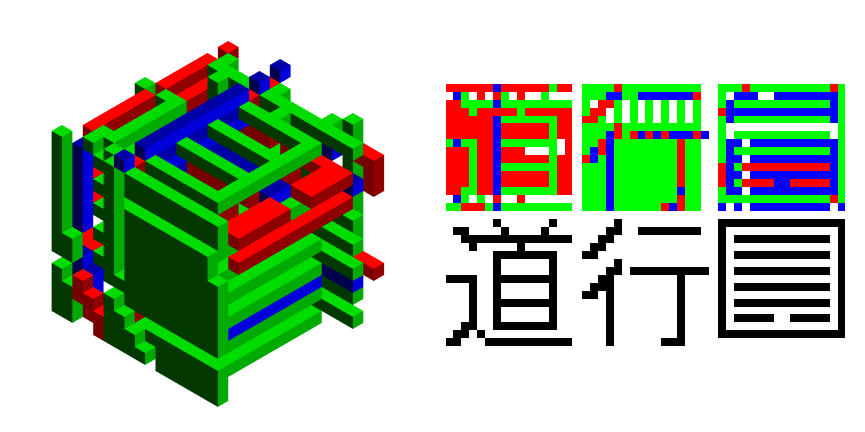
Show[Trigram@SymCryptograms[[1]], ImageSize -> 800]

The symmetry is obviously preserved, with only one plane of reflection through edge midpoints ( $xy$ if $z$ is up). One important question is whether or not you can find a statistical test that says such a graph is not just an Autoglyph in 3D? If yes, this could potentially lead to a decryption algorithm for actually discovering secret keys, or at least the secret pads. Let's see one more encrypt / decrypt pair, of course, this time with Octahedral symmetry (as in the animation above):
decsTest = SymDecode[SymCryptograms[[3]], #] & /@ AGTests;
Length /@ decsTest
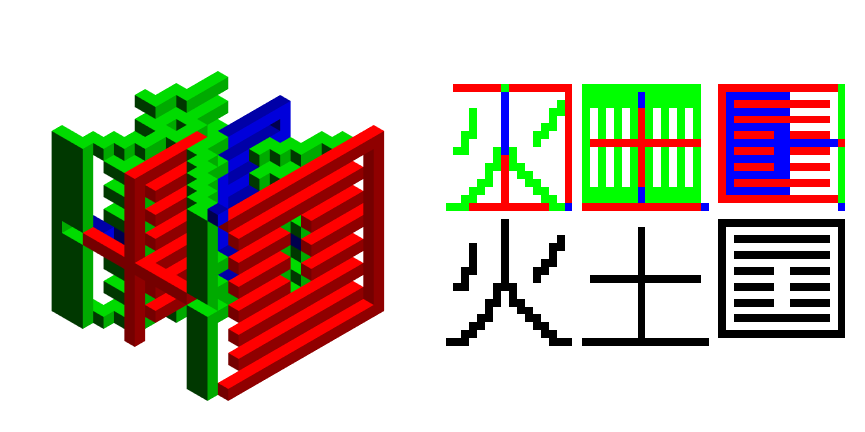
Show[Trigram@SymCryptograms[[3]], ImageSize -> 800]
Column[RGBBWResults /@ decsTest[[8]]]
Out[]={2, 2, 2, 2, 2, 2, 2, 1}

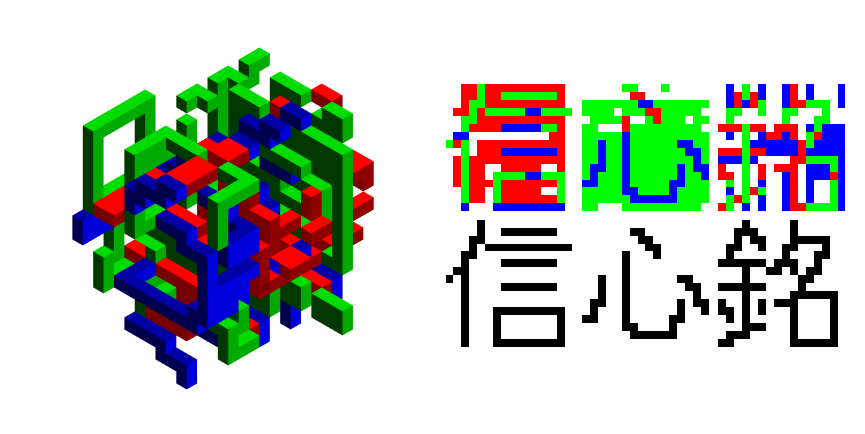
Okay, that's all the hints I can give you for now. If you are practicing for the upcoming new years challenge, please complete index maps for the first and second dataset. You can even post them here if you want. We will return shortly with more encrypted data and rules for the competition New Year Water Tiger 2022.