
I recently joined in the fun of making an NFT and created the art set 'Electrum Anatomy'. It can be found on OpenSea here: https://opensea.io/collection/electrum-anatomy.
This collection contains images of various anatomical systems of human, horse, and dog -- all obtained through AnatomyData. The aesthetic is low-polygon, metallic, glowing, and a touch of a vaporwave color scheme. For each species, the collection contains separate images of bones, channels, muscles, and organs.
In this post I'd like to walk you through how these images were created, but first here's a few select images from the collection (click for higher resolution):
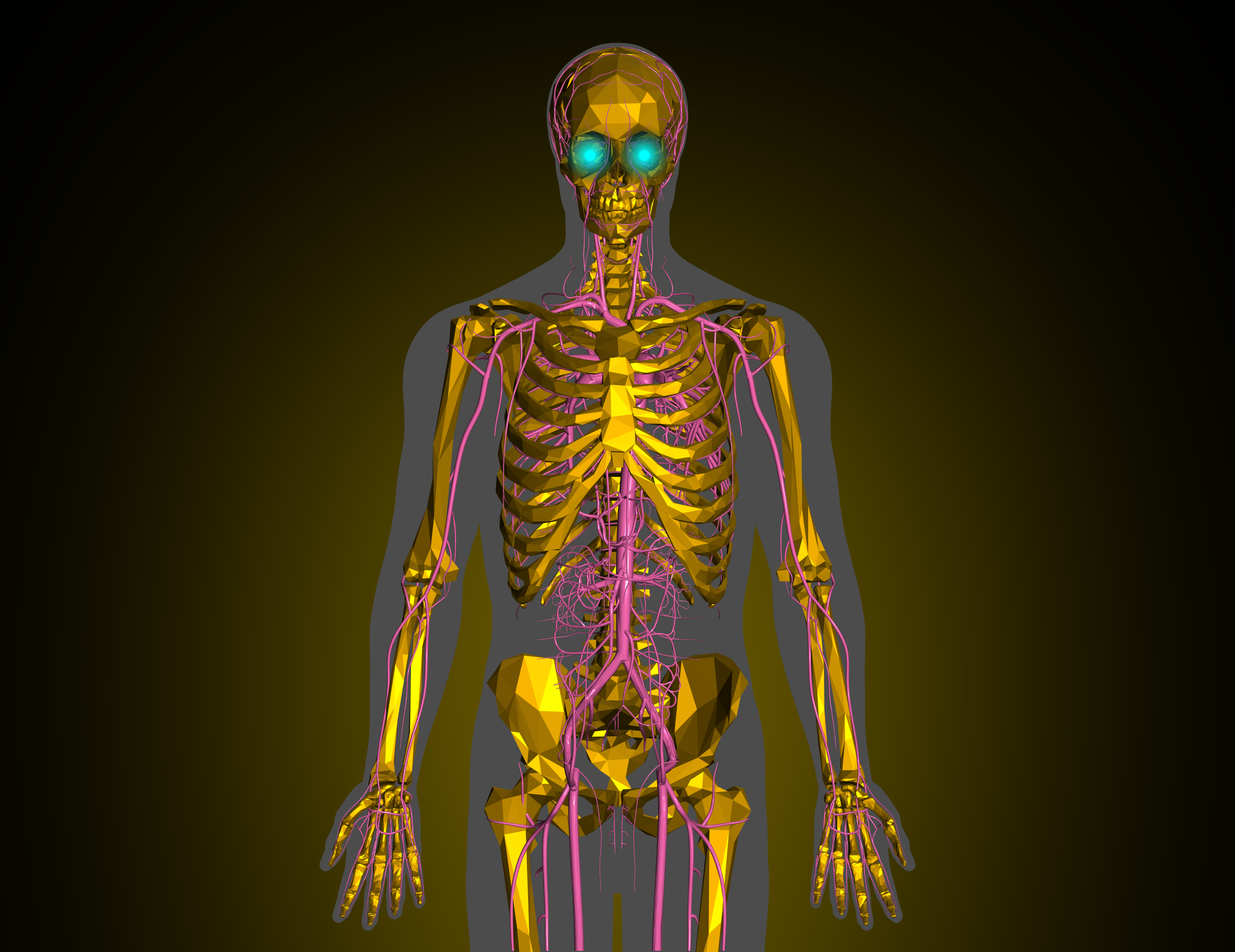
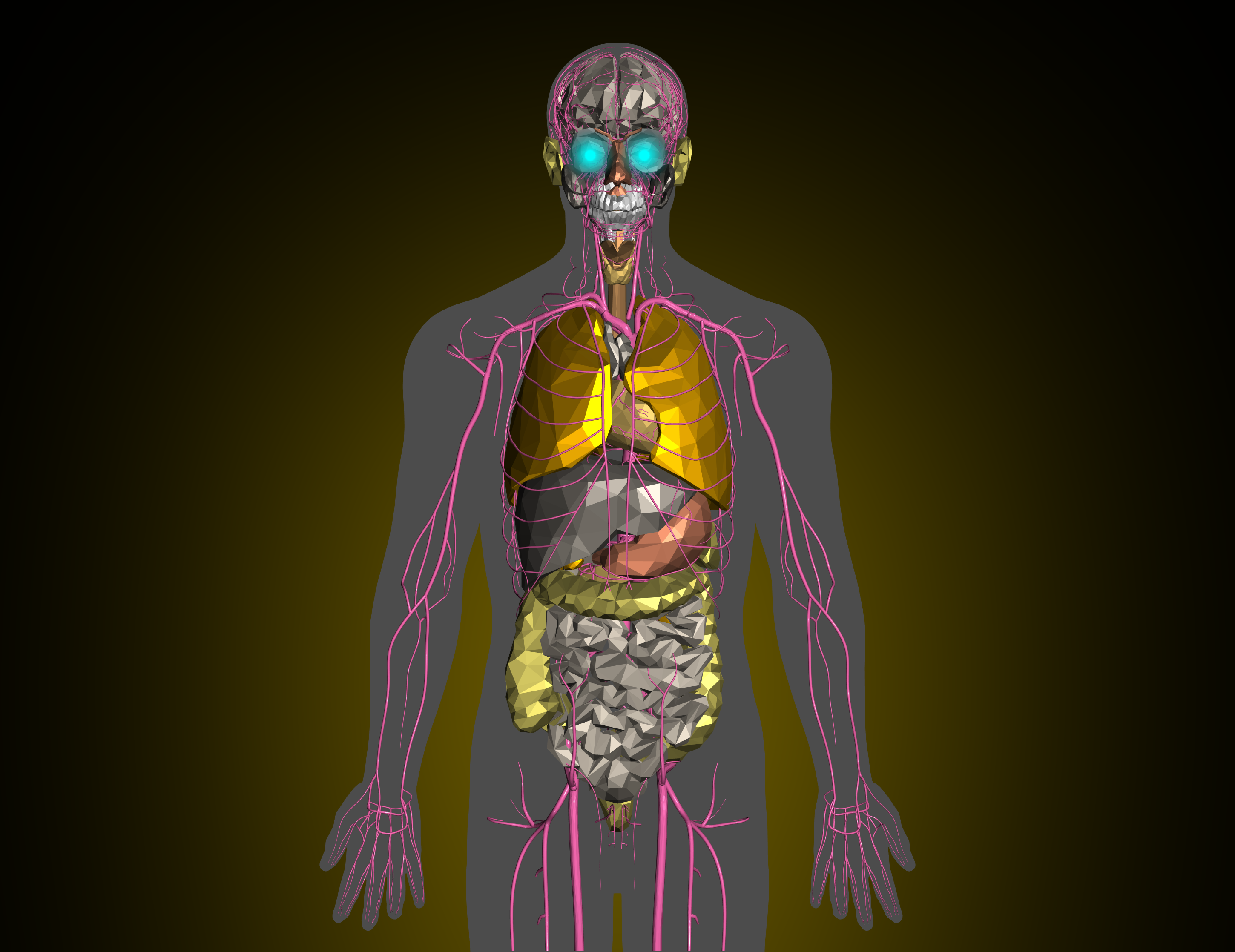
I'll walk through a simple example of rendering a gold skull with glowing eyes. The images listed on OpenSea have a few extra details and nuances that I'll gloss over in this post.
Obtaining anatomical data
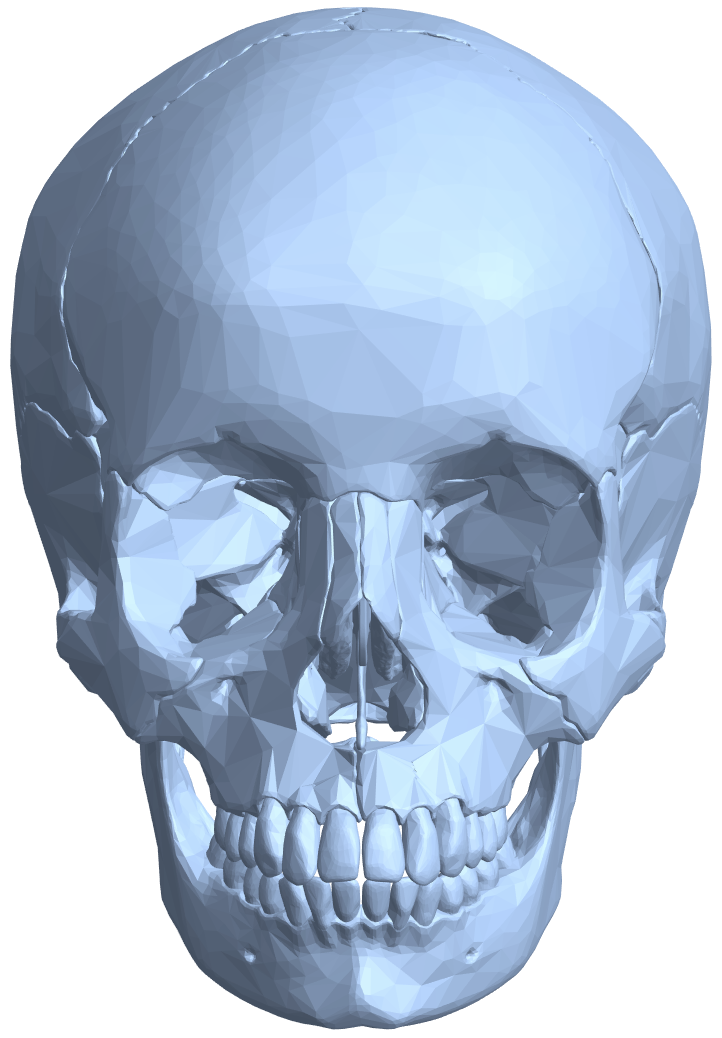
Obtaining the 3D anatomical data was quite easy. A simple property lookup:
skull = Entity["AnatomicalStructure", "Skull"]["MeshRegion"]
Downsampling a mesh
The aesthetic I was after called for low-polygon meshes, so the next task was to simplify the meshes from AnatomyData. For this I implemented a bare-bones (pun intended) version of the algorithm presented in Surface Simplification Using Quadric Error Metrics, Garland et.al. The function, decimateMesh, takes in a mesh and the number of vertices to contract from the mesh. I plan to submit this to WFR once I flush out more details like handling boundaries differently, always preserving topology, and an optional bias to simplify planar regions less. I've attached the code for decimateMesh below.
Here's a simple example. Let's contract 2650 vertices from a triceratops model:
mr = ExampleData[{"Geometry3D", "Triceratops"}, "MeshRegion"];
mr2 = decimateMesh[mr, 2650];
We went from 5660 triangles to only 360:
MeshCellCount /@ {mr, mr2}
(* {{2832, 8490, 5660}, {182, 540, 360}} *)
And a visual comparison: 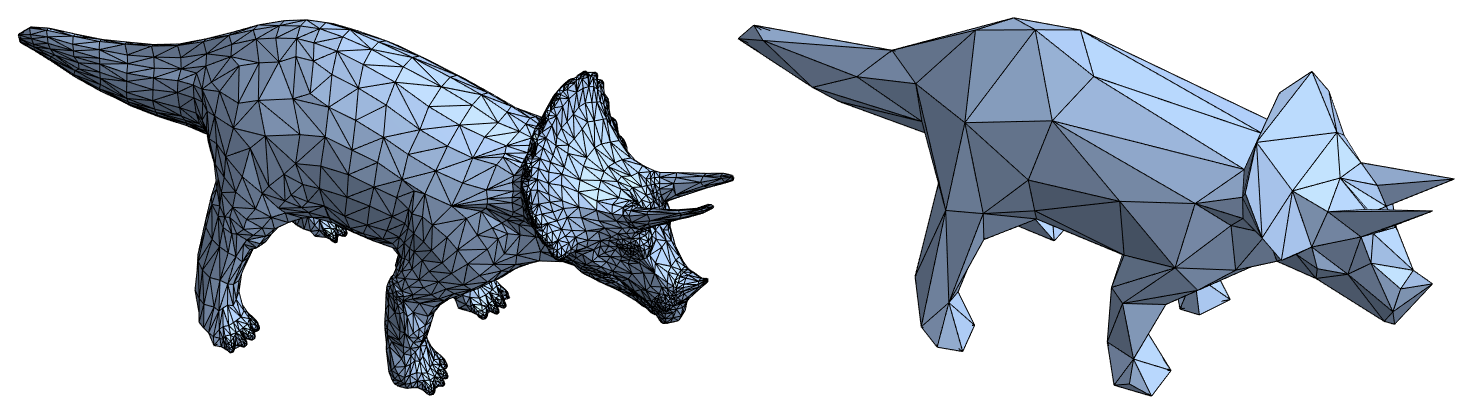
Let's contract 96% of the skull's vertices to give it that low-poly feel:
dskull = decimateMesh[skull, Scaled[0.96]]

Glowing eyes
To make glowing eyes, I first took a RadialGradientImage, then clipped, rescaled, and blurred it. Finally I colored it cyan, all while preserving an appropriate alpha channel:
clip = 0.9;
grad = RadialGradientImage[{White, GrayLevel[0.8], Gray, Black, Black, Black}];
grad2 = Blur[ImageAdjust[(Clip[grad, {0, clip}, {0, clip + .05}]/clip)^1.5]];
geye = SetAlphaChannel[ImageMultiply[grad2, Cyan], grad]

Rendering
MaterialShading was used to render each 3D object over a black background. For the muscle and organ images, each object was randomly shaded with one of
{"Aluminum", "Brass", "Bronze", "Copper", "Electrum", "Gold", "Iron", "Pewter", "Silver"}
Once rasterized, ImageCompose was used to overlay the glowing eyes.
gskull = Graphics3D[
GraphicsComplex[
MeshCoordinates[dskull],
{MaterialShading["Gold"], MeshCells[dskull, 2, "Multicells" -> True]}
],
Background -> Black,
Boxed -> False,
ImageSize -> 700,
Lighting -> "ThreePoint",
ViewPoint -> {0, -100, 0},
ViewVertical -> {0, 0, 1}
];
imskull = Rasterize[gskull, Background -> None];
imskulleyes = ImageCompose[
ImageCompose[
imskull,
ImageResize[geye, Scaled[5]],
Scaled[{.3, .44}]
],
ImageResize[geye, Scaled[5]],
Scaled[{.7, .44}]
];
RemoveAlphaChannel[imskulleyes]

Glowing background
The glowing background was obtained by simply blurring the alpha mask and coloring it gold.
mask = FillingTransform[AlphaChannel[imskulleyes2]];
blur = Blur[mask, 1000];
bg = ImageMultiply[ImageAdjust[blur, {0, 0, 0.75}], ColorData["HTML"]["Gold"]];
bg = ImageMultiply[bg, ColorNegate[mask]];
skullfinal = ImagePad[ImageCompose[bg, imskulleyes2], {{-200, -200}, {-600, -600}}]

Happy NFTing!
 Attachments:
Attachments: