what is `v` in `y = v` ? assuming this is a typo and it is meant to be `u` then
ClearAll[u]
ParametricPlot3D[{2 Sinh[u], u, 2 Cosh[u]}, {u, -Pi/4, Pi/4}, PlotStyle -> {Thick, Red}, AxesLabel -> {x, y, z}]
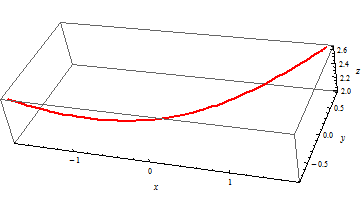
For y=v then
ClearAll[u, v]
ParametricPlot3D[{2 Sinh[u], v, 2 Cosh[u]}, {u, -Pi/4, Pi/4}, {v, -Pi/4, Pi/4}, PlotStyle -> {Thick, Red}, AxesLabel -> {x, y, z}]
