Jairo,
I do not know the inner workings for PIDTune, however, it appears to have difficulty with the derivative for a system with such a long time delay. If you use a PI controller with some options, you get a reasonable response. For example,
Gc = PIDTune[gf, {"PI", "AMIGO"}, "ReferenceOutput"];
out1 = OutputResponse[Gc, UnitStep[t], {t, 0, 1000}];
Plot[out1, {t, 0, 1000}, PlotRange -> All]
Takes the open loop response of
Plot[Evaluate@
OutputResponse[gf, UnitStep[t]/13.138, {t, 0, 1000}], {t, 0, 1000},
PlotRange -> All]
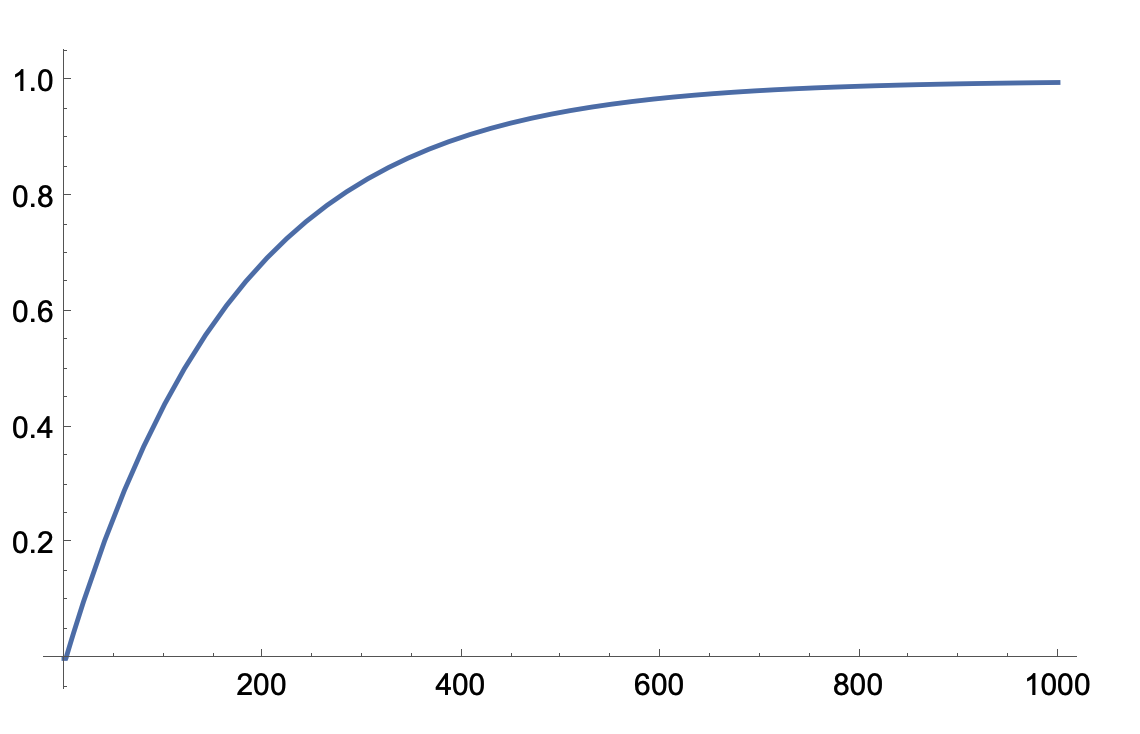
and turns it into this:
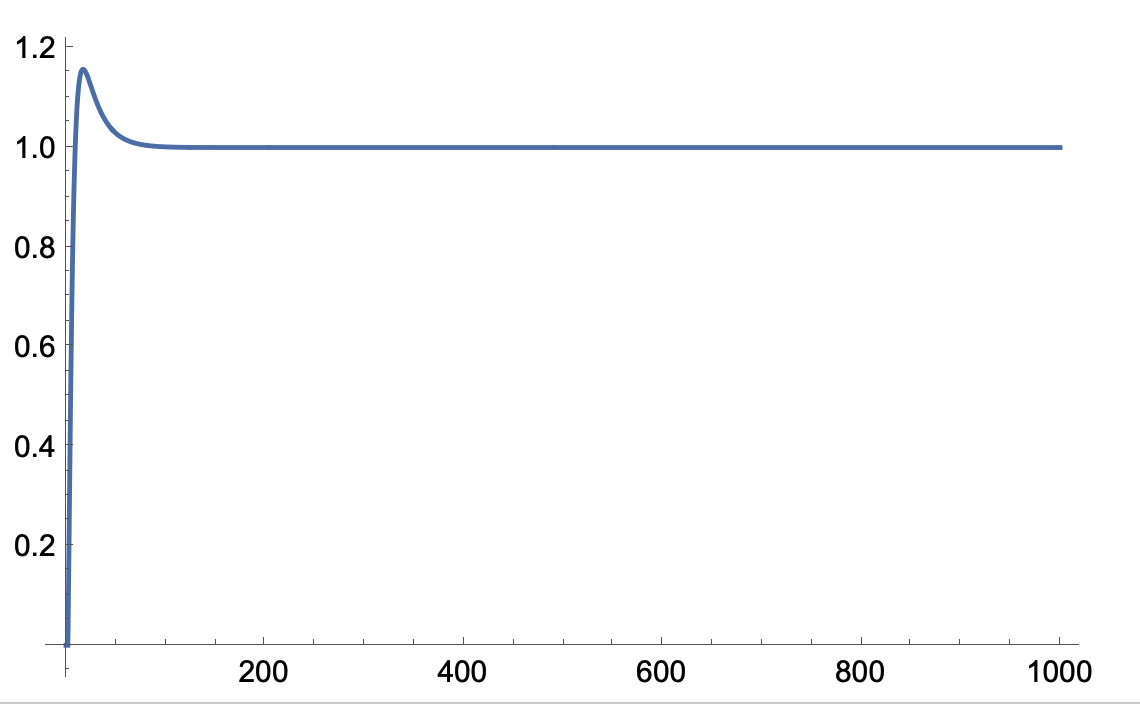
You can try different options to get different responses. If I were hand tuning it, I would tend to slow the system down more and get rid of the overshoot. I'm not sure why the PIDTune results are more oscillatory (especially with the default options). For details of why the addition of the derivative creates an unstable system and why the tune is not particularly good, I would see if @Suba Thomas has any insight that would help. It is generally difficult to use derivative action in a PID controller when the time delay is significant.
Regards
Neil