This algorithm is 3D extension of our 2D algorithm published on this page and here. We suppose that with this code we can simulate transition from laminar to turbulent flow. In this example we compute viscous flow around cuboid at Reynolds number $Re=6250$. Note, that code has been tested up to $Re=10^6$.
dif = 1/6250; pec = .72; U0 = 1.; V0 = 0.; W0 = 0.; dn0 = 1.; n = 80;
n1 = n + 1; sm = 500; r = 20; den = ConstantArray[dn0 , {n1, n1, n1}];
u0 = ConstantArray[U0, {n1, n1, n1}];
v0 = ConstantArray[V0, {n1, n1, n1}]; w0 =
ConstantArray[W0, {n1, n1, n1}]; Do[u0[[i, j, k]] = 0;
v0[[i, j, k]] = 0;
w0[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
periodic[n_, up_, ud_, ul_, ur_, ub_] :=
Module[{bd = ub},
Do[bd[[n + 1, i, j]] = bd[[2, i, j]];
bd[[1, i, j]] = bd[[n, i, j]];, {i, 2, n}, {j, 2, n}];
Do[bd[[i, 1, j]] = ud;
bd[[i, n + 1, j]] = up; bd[[i, j, 1]] = ul;
bd[[i, j, n + 1]] = ur;, {i, 1, n + 1}, {j, 1, n + 1}];
bd];
diffuse[n_, r_, a_, c_, c0_] :=
Module[{c1 = c},
Do[Do[Do[
Do[c1[[i, j,
k]] = (c0[[i, j, k]] +
a (c1[[i - 1, j, k]] + c1[[i + 1, j, k]] +
c1[[i, j - 1, k]] + c1[[i, j + 1, k]] +
c1[[i, j, k - 1]] + c1[[i, j, k + 1]]))/(1 +
6 a);, {k, 2, n}];, {j, 2, n}];, {i, 2, n}];
Do[c1[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5],
1}];, {k1, 0, r}];
c1];
advect[n_, d0_, u_, v_, w_, dt_] :=
Module[{x, y, z, d1, dt0, i0, i1, j0, j1, k0, k1, s0, s1, t0, t1,
p1, p0, d000, d100, d010, d001, d110, d011, d101, d111},
d1 = ConstantArray[0, {n + 1, n + 1, n + 1}]; dt0 = dt n;
Do[Do[Do[x = i - dt0 u[[i, j, k]]; y = j - dt0 v[[i, j, k]];
z = k - dt0 w[[i, j, k]];
i0 = Which[x <= 1, 1, 1 < x < n, Floor[x], True, n];
i1 = i0 + 1;
j0 = Which[y <= 1, 1, 1 < y < n, Floor[y], True, n];
j1 = j0 + 1;
k0 = Which[z <= 1, 1, 1 < z < n, Floor[z], True, n];
k1 = k0 + 1;
d000 = (d0[[i0, j0,
k0]] + (x - i0) (d0[[i1, j0, k0]] -
d0[[i0, j0, k0]]) + (y - j0) (d0[[i0, j1, k0]] -
d0[[i0, j0, k0]]) + (z - k0) (d0[[i0, j0, k1]] -
d0[[i0, j0, k0]]));
d100 = (d0[[i1, j0,
k0]] + (x - i1) (d0[[i1, j0, k0]] -
d0[[i0, j0, k0]]) + (y - j0) (d0[[i1, j1, k0]] -
d0[[i1, j0, k0]]) + (z - k0) (d0[[i1, j0, k1]] -
d0[[i1, j0, k0]]));
d010 = (d0[[i0, j1,
k0]] + (x - i0) (d0[[i1, j1, k0]] -
d0[[i0, j1, k0]]) + (y - j1) (d0[[i0, j1, k0]] -
d0[[i0, j0, k0]]) + (z - k0) (d0[[i0, j1, k1]] -
d0[[i0, j1, k0]]));
d001 = (d0[[i0, j0,
k1]] + (x - i0) (d0[[i1, j0, k1]] -
d0[[i0, j0, k1]]) + (y - j0) (d0[[i0, j1, k1]] -
d0[[i0, j0, k1]]) + (z - k1) (d0[[i0, j0, k1]] -
d0[[i0, j0, k0]]));
d110 = (d0[[i1, j1,
k0]] + (x - i1) (d0[[i1, j1, k0]] -
d0[[i0, j1, k0]]) + (y - j1) (d0[[i1, j1, k0]] -
d0[[i1, j0, k0]]) + (z - k0) (d0[[i1, j1, k1]] -
d0[[i1, j1, k0]]));
d011 = (d0[[i0, j1,
k1]] + (x - i0) (d0[[i1, j1, k1]] -
d0[[i0, j1, k1]]) + (y - j1) (d0[[i0, j1, k1]] -
d0[[i0, j0, k1]]) + (z - k1) (d0[[i0, j1, k1]] -
d0[[i0, j1, k0]]));
d101 = (d0[[i1, j0,
k1]] + (x - i1) (d0[[i1, j0, k1]] -
d0[[i0, j0, k1]]) + (y - j0) (d0[[i1, j1, k1]] -
d0[[i1, j0, k1]]) + (z - k1) (d0[[i1, j0, k1]] -
d0[[i1, j0, k0]]));
d111 = (d0[[i1, j1,
k1]] + (x - i1) (d0[[i1, j1, k1]] -
d0[[i0, j1, k1]]) + (y - j1) (d0[[i1, j1, k1]] -
d0[[i1, j0, k1]]) + (z - k1) (d0[[i1, j1, k1]] -
d0[[i1, j1, k0]]));
d1[[i, j,
k]] = (d000 + d100 + d010 + d001 + d110 + d011 + d101 +
d111)/8;, {k, 2, n}];, {j, 2, n}];, {i, 1, n + 1}]; d1];
project[n_, r_, u0_, v0_, w0_, u_, v_, w_] :=
Module[{ux = u, vy = v, wz = w, div, p},
p = ConstantArray[0, {n + 1, n + 1, n + 1}];
div = ConstantArray[0, {n + 1, n + 1, n + 1}];
ux = ConstantArray[0, {n + 1, n + 1, n + 1}];
vy = ConstantArray[0, {n + 1, n + 1, n + 1}];
wz = ConstantArray[0, {n + 1, n + 1, n + 1}];
Do[div[[i, j,
k]] = .5/
n (u0[[i + 1, j, k]] - u0[[i - 1, j, k]] + v0[[i, 1 + j, k]] -
v0[[i, j - 1, k]] + w0[[i, j, k + 1]] -
w0[[i, j, k - 1]]);, {i, 2, n}, {j, 2, n}, {k, 2, n}];
Do[div[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
div = periodic[n, 0, 0, 0, 0, div];
Do[Do[Do[
Do[p[[i, j,
k]] = (div[[i, j,
k]] + (p[[i - 1, j, k]] + p[[i + 1, j, k]] +
p[[i, j - 1, k]] + p[[i, j + 1, k]] +
p[[i, j, k - 1]] + p[[i, j, k + 1]]))/6;, {k, 2,
n}];, {j, 2, n}], {i, 2, n}];, {k1, 0, r}];
Do[p[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
p = periodic[n, 0, 0, 0, 0, p];
Do[ux[[i, j, k]] =
u0[[i, j, k]] + .5 n (p[[i + 1, j, k]] - p[[i - 1, j, k]]);
vy[[i, j, k]] =
v0[[i, j, k]] + .5 n (p[[i, j + 1, k]] - p[[i, j - 1, k]]);
wz[[i, j, k]] =
w0[[i, j, k]] + .5 n (p[[i, j, k + 1]] - p[[i, j, k - 1]]);, {i,
2, n}, {j, 2, n}, {k, 2, n}];
Do[ux[[i, j, k]] = 0; vy[[i, j, k]] = 0;
wz[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}]; {ux,
vy, wz}];
onestep[n_, step_, r_, a_, uin_, vin_, win_, dt_, c_] :=
Module[{u1, v1, w1, u, v, w, u0, v0, w0},
u0 = ConstantArray[0., {n + 1, n + 1, n + 1}];
v0 = ConstantArray[0., {n + 1, n + 1, n + 1}];
w0 = ConstantArray[0., {n + 1, n + 1, n + 1}];
u = ConstantArray[0., {n + 1, n + 1, n + 1}];
v = ConstantArray[0., {n + 1, n + 1, n + 1}];
w = ConstantArray[0., {n + 1, n + 1, n + 1}];
u1 = ConstantArray[0., {n + 1, n + 1, n + 1}];
v1 = ConstantArray[0., {n + 1, n + 1, n + 1}];
w1 = ConstantArray[0., {n + 1, n + 1, n + 1}]; u0 = uin; v0 = vin;
w0 = win;
Do[u0[[i, j, k]] = 0; v0[[i, j, k]] = 0;
w0[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
u0 = advect[n, u0, u0, v0, w0, dt];
v0 = advect[n, v0, u0, v0, w0, dt];
w0 = advect[n, w0, u0, v0, w0, dt];
Do[u0[[i, j, k]] = 0;
v0[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
u0 = periodic[n, 0, 0, 0, 0, u0]; v0 = periodic[n, 0, 0, 0, 0, v0];
w0 = periodic[n, 0, 0, 0, 0, w0];
u0 = diffuse[n, r, a, c, u0]; v0 = diffuse[n, r, a, c, v0];
w0 = diffuse[n, r, a, c, w0];
Do[u0[[i, j, k]] = 0; v0[[i, j, k]] = 0;
w0[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
u0 = periodic[n, 0, 0, 0, 0, u0]; v0 = periodic[n, 0, 0, 0, 0, v0];
w0 = periodic[n, 0, 0, 0, 0, w0];
{u0, v0, w0} = project[n, r, u0, v0, w0, u, v, w];
Do[u0[[i, j, k]] = 0; v0[[i, j, k]] = 0;
w0[[i, j, k]] = 0;, {i, 10, 20, 1}, {j, Round[n/2 - 5],
Round[n/2 + 5], 1}, {k, Round[n/2 - 5], Round[n/2 + 5], 1}];
u0 = periodic[n, 0, 0, 0, 0, u0]; v0 = periodic[n, 0, 0, 0, 0, v0];
w0 = periodic[n, 0, 0, 0, 0, w0]; {u0, v0, w0}]
cf = With[{cg = Compile`GetElement, hp = HoldPattern,
dv = DownValues},
Hold@Compile[{{u0argu, _Real, 3}, {v0argu, _Real,
3}, {w0argu, _Real, 3}, {denargu, _Real,
3}, {sm, _Integer}, {n, _Integer}, {r, _Integer}, dif,
pec}, Module[{u0 = u0argu, v0 = v0argu, w0 = w0argu, uu,
vv, ww, dd, den = denargu,
c = Table[0., {n + 1}, {n + 1}, {n + 1}], dt = 40./n^2,
a, dnup = den[[1, n + 1, 1]], dnd = den[[1, 1, 1]],
dnl = den[[1, 1, 1]], dnr = den[[1, 1, n + 1]]},
a = dt dif n n;
uu = vv =
ww = dd =
Table[0., {sm + 1}, {n + 1}, {n + 1}, {n + 1}];
Do[{u0, v0, w0} =
onestep[n, step, r, a, u0, v0, w0, dt, c];
uu[[step + 1]] = u0;
vv[[step + 1]] = v0; ww[[step + 1]] = w0;
den = diffuse[n, r, a/pec, c, den];
Do[den[[i, j, k]] = 0;, {i, 10, 20, 1}, {j,
Round[n/2 - 5], Round[n/2 + 5], 1}, {k,
Round[n/2 - 5], Round[n/2 + 5], 1}];
den = periodic[n, dnup, dnd, dnl, dnr, den];
den = advect[n, den, u0, v0, w0, dt];
Do[den[[i, j, k]] = 0;, {i, 10, 20, 1}, {j,
Round[n/2 - 5], Round[n/2 + 5], 1}, {k,
Round[n/2 - 5], Round[n/2 + 5], 1}];
den = periodic[n, dnup, dnd, dnl, dnr, den];
dd[[step + 1]] = den;, {step, 0, sm}]; {uu, vv, ww,
dd}], CompilationTarget -> "C",
RuntimeOptions -> "Speed"] /. dv@onestep /.
Flatten[dv /@ {advect, diffuse, periodic, project}] /.
hp@ConstantArray[c_, {i_, j_, kc_}] :>
Table[0., {i}, {j}, {kc}] /. hp@Part[a__] :> cg[a] /.
hp[cg[a__] = rhs_] :> (Part[a] = rhs) //
ReleaseHold];
rst = cf[u0, v0, w0, den, sm, n, r, dif, pec];
Visualization
Do[lst11[s] =
Table[{{(i - 1)/n, (j - 1)/n, (k - 1)/n}, rst[[1, s, i, j, k]]}, {i,
n1}, {j, n1}, {k, n1}];
lst12[s] =
Table[{{(i - 1)/n, (j - 1)/n, (k - 1)/n}, rst[[2, s, i, j, k]]}, {i,
n1}, {j, n1}, {k, n1}];
lst13[s] =
Table[{{(i - 1)/n, (j - 1)/n, (k - 1)/n}, rst[[3, s, i, j, k]]}, {i,
n1}, {j, n1}, {k, n1}];, {s, 25, sm, 25}]
Do[su1[i] =
Interpolation[Flatten[lst11[i], 2], InterpolationOrder -> 3];
sv2[i] = Interpolation[Flatten[lst12[i], 2],
InterpolationOrder -> 3];
sw3[i] = Interpolation[Flatten[lst13[i], 2],
InterpolationOrder -> 3];, {i, 25, sm, 25}]
Table[Show[
DensityPlot3D[
Norm[{su1[i][x, y, z], sv2[i][x, y, z], sw3[i][x, y, z]}], {x, 0,
1}, {y, 0.44, 1}, {z, 0, 1}, BoxRatios -> Automatic,
ColorFunction -> "BlueGreenYellow", PlotLabel -> i],
VectorPlot3D[{su1[i][x, y, z], sv2[i][x, y, z],
sw3[i][x, y, z]}, {x, 0, 1}, {y, 0, .5}, {z, 0, 1},
VectorPoints -> Fine, VectorMarkers -> "Arrow"],
Graphics3D[{{Blue,
Cuboid[{10, Round[n/2 - 5] - 1/2,
Round[n/2 - 5] - 1/2}/(n + 1), {20, Round[n/2 + 5] - 1/2,
Round[n/2 + 5] - 1/2}/(n + 1)]}}]], {i, 50, sm, 50}]
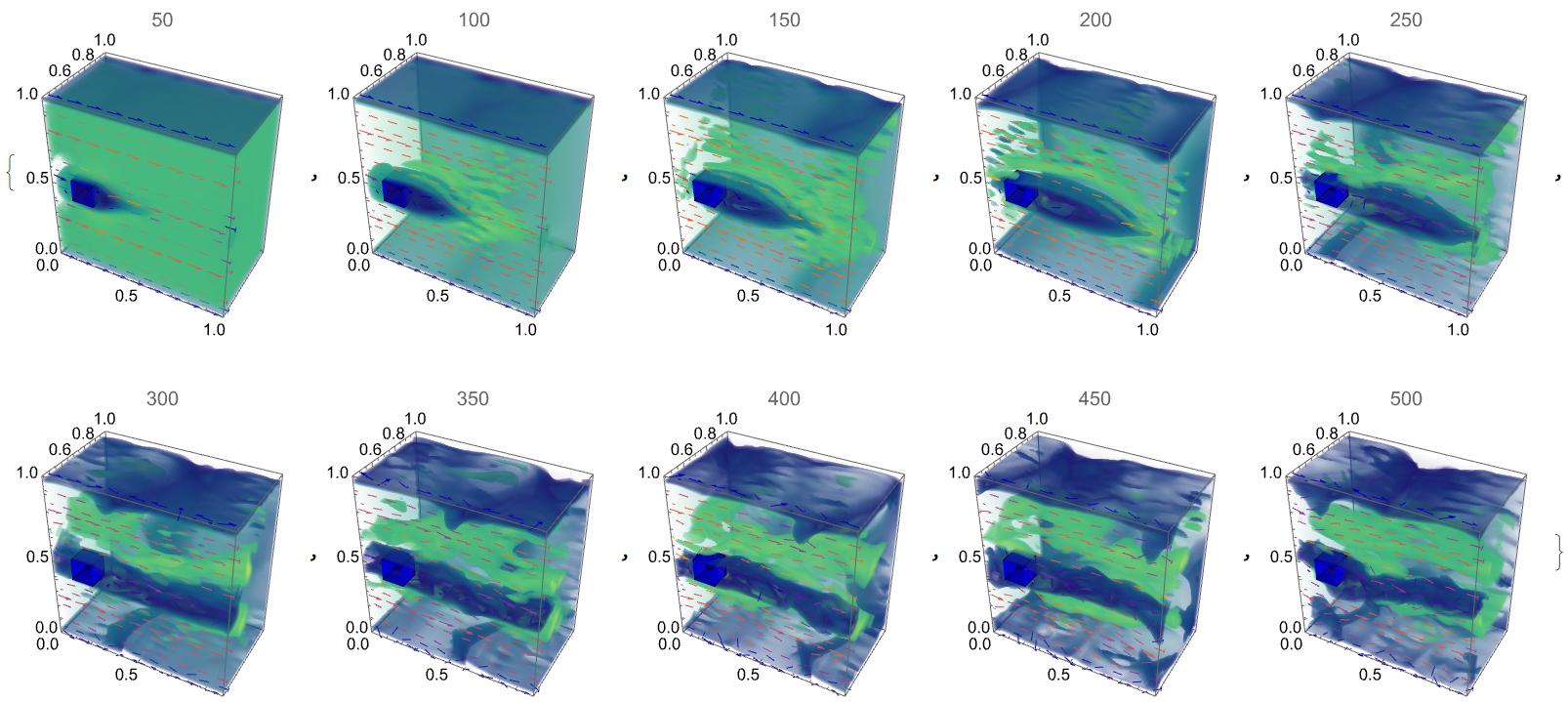
Animation
Do[lstu1[k] =
Flatten[Table[{{(i - 1)/n, (j - 1)/n},
rst[[1, k, i, Round[(n + 1)/2], j]]}, {i, n1}, {j, n1}], 1];
lstw1[k] =
Flatten[Table[{{(i - 1)/n, (j - 1)/n},
rst[[2, k, i, Round[(n + 1)/2], j]]}, {i, n1}, {j, n1}],
1];, {k, sm}];
Do[Uvel1[i] = Interpolation[lstu1[i], InterpolationOrder -> 3];, {i,
1, sm}];
Do[Wvel1[i] = Interpolation[lstw1[i], InterpolationOrder -> 3];, {i,
1, sm}];
frame = Table[
Show[DensityPlot[
Norm[{Uvel[m][x, y], Vvel[m][x, y]}], {x, 0, 1}, {y, 0, 1},
PlotRange -> All, ColorFunction -> "BlueGreenYellow",
Frame -> False, ImageSize -> Tiny, PlotLabel -> m,
PlotPoints -> 50],
Graphics[{Gray,
Rectangle[{10, Round[n/2 - 5] - 1/2}/(n + 1), {20,
Round[n/2 + 5] - 1/2}/(n + 1)]}]], {m, 5, sm, 3}];

The question is about code improvement. How can we define parameter r to solve Laplace and Poison equations in this code? Note, r is number of iterations in diffuse and project module (we use Gauss-Seidel relaxation to solve Laplace and Poison's equations).
Update 1. We can reduce r from r=20 as above to r=5 as below. Globally there is no difference in two animations.

But if we compare velocity in some point like $x=0.65, y=0.5$ then we have good agreement for $r=5$ (red points) and $r=20$ (gray points) in laminar flow at $t<0.5$, but a big difference in the turbulent flow at $t>0.5$.
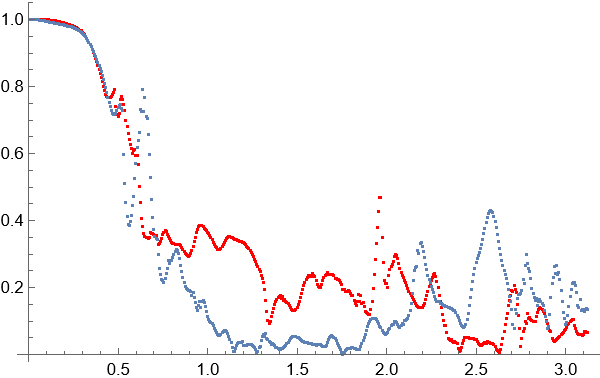
Update 1. To test the Gauss-Seidel relaxation method itself we can compute viscous flow in a plane channel with external force (gravity) as follows
ClearAll["Global`*"]
dif = 1/80; pec = 1; U0 = 0; V0 = 0; n = 11; n1 = n + 1; dt =
2./n^2; sm = 3000; r = 7; n2 = Round[n/2]; a = dt dif n n; c =
ConstantArray[0, {n1, n1}]; c0 = ConstantArray[0, {n1, n1}];; u0 =
ConstantArray[0, {n1, n1}]; v0 = ConstantArray[0, {n1, n1}]; u =
ConstantArray[0, {n1, n1}]; v = ConstantArray[0, {n1, n1}];
periodic[n_, up_, ud_, ub_] :=
Module[{bd = ub},
Do[bd[[1, i]] = .5 (bd[[n, i]] + bd[[2, i]]);
bd[[n + 1, i]] = bd[[1, i]]; bd[[i, 1]] = ud;
bd[[i, n + 1]] = up;, {i, 2, n}]; bd[[1, 1]] = ud;
bd[[n + 1, n + 1]] = up; bd[[n + 1, 1]] = ud; bd[[1, n + 1]] = up;
bd];
diffuse[n_, r_, a_, c_, c0_] :=
Module[{c1 = c}, c1 = ConstantArray[0, {n + 1, n + 1}];
Do[Do[Do[c1[[i,
j]] = (c0[[i, j]] +
a (c1[[i - 1, j]] + c1[[i + 1, j]] + c1[[i, j - 1]] +
c1[[i, j + 1]]))/(1 + 4 a);, {j, 2, n}];, {i, 2, n}];
c1 = periodic[n, 0, 0, c1];, {k, 0, r}]; c1];
advect[n_, b_, d_, d0_, u_, v_, dt_] :=
Module[{x, y}, d1 = ConstantArray[0, {n + 1, n + 1}]; dt0 = dt n;
Do[Do[x = i - dt0 u[[i, j]]; y = j - dt0 v[[i, j]];
i0 = Which[x <= 1, 1, 1 < x < n, Floor[x], x >= n, n];
i1 = i0 + 1;
j0 = Which[y <= 1, 1, 1 < y < n, Floor[y], y >= n, n];
j1 = j0 + 1; s1 = x - i0; s0 = 1 - s1; t1 = y - j0; t0 = 1 - t1;
d1[[i, j]] =
s0 (t0 d0[[i0, j0]] + t1 d0[[i0, j1]]) +
s1 (t0 d0[[i1, j0]] + t1 d0[[i1, j1]]);, {j, 1, n + 1}];, {i,
1, n + 1}]; d1];
project[n_, r_, u0_, v0_, u_, v_] :=
Module[{ux = u, vy = v}, p = ConstantArray[0, {n1, n1}];
div = ConstantArray[0, {n1, n1}]; ux = ConstantArray[0, {n1, n1}];
vy = ConstantArray[0, {n1, n1}];
Do[div[[i,
j]] = -.5 /
n (u0[[i + 1, j]] - u0[[i - 1, j]] + v0[[i, 1 + j]] -
v0[[i, j - 1]]);, {i, 2, n}, {j, 2, n}];
Do[Do[Do[
p[[i, j]] = (div[[i,
j]] + (p[[i - 1, j]] + p[[i + 1, j]] + p[[i, j - 1]] +
p[[i, j + 1]]))/4;, {j, 2, n}], {i, 2, n}];, {k, 0, r}];
Do[ux[[i, j]] = u0[[i, j]] - .5 n (p[[i + 1, j]] - p[[i - 1, j]]);
vy[[i, j]] =
v0[[i, j]] - .5 n (p[[i, j + 1]] - p[[i, j - 1]]);, {i, 2,
n}, {j, 2, n}]; {ux, vy}];
(*force*)
Fx[t_, x_, y_] := 1/10; Fy[t_, x_, y_] := 0;
f1 = ConstantArray[0, {n1, n1}]; f2 = ConstantArray[0, {n1, n1}];
Do[u0 = advect[n, 0, c, u0, u0, v0, dt];
v0 = advect[n, 0, c, v0, u0, v0, dt];
u0 = periodic[n, 0, 0, u0]; v0 = periodic[n, 0, 0, v0];
u0 = diffuse[n, r, a, c, u0]; v0 = diffuse[n, r, a, c, v0];
u0 = periodic[n, 0, 0, u0]; v0 = periodic[n, 0, 0, v0];
Do[f1[[i, j]] = Fx[dt (step + .5), (i - 1)/n, (j - 1)/n];
f2[[i, j]] = Fy[dt (step + .5), (i - 1)/n, (j - 1)/n];, {i, 2,
n1}, {j, 2, n1}]; u0 += f1 dt;
v0 += f2 dt; {u0, v0} = project[n, r, u0, v0, u, v];
u0 = periodic[n, 0, 0, u0]; v0 = periodic[n, 0, 0, v0];
uu[step] = u0; vv[step] = v0;, {step, 0, sm}];
Visualization of flow velocity and absolute error
Do[lstu[k] =
Flatten[Table[{{(i - 1)/n, (j - 1)/n}, uu[k][[i, j]]}, {i, n1}, {j,
n1}], 1];
lstv[k] =
Flatten[Table[{{(i - 1)/n, (j - 1)/n}, vv[k][[i, j]]}, {i, n1}, {j,
n1}], 1];, {k, 0, sm}];
Do[Uvel[i] = Interpolation[lstu[i], InterpolationOrder -> 3];, {i, 1,
sm}]
Do[Vvel[i] = Interpolation[lstv[i], InterpolationOrder -> 3];, {i, 1,
sm}];
{StreamDensityPlot[{Uvel[sm][x, y], Vvel[sm][x, y]}, {x, 0, 1}, {y, 0,
1}, ColorFunction -> "RoseColors", Frame -> False,
PlotLegends -> Automatic],
Plot3D[Uvel[sm][x, y], {x, 0, 1}, {y, 0, 1},
ColorFunction -> "RoseColors"]}
{ListPlot[Table[{i dt, Max[uu[i]]}, {i, sm}],
AxesLabel -> {"t", "Umax"}],
Plot[{-4 (-y + y^2), Uvel[sm][.5, y]}, {y, 0, 1},
PlotStyle -> {Thick, {Red, Dashed}}, Frame -> True,
FrameLabel -> {"y", "u"},
PlotLegends -> {"Exact solution", "Numeric solution"}],
Plot[Abs[-Uvel[sm][.5, y] - 4 (-y + y^2)], {y, 0, 1}, Frame -> True,
FrameLabel -> {"y", "Error"}]}
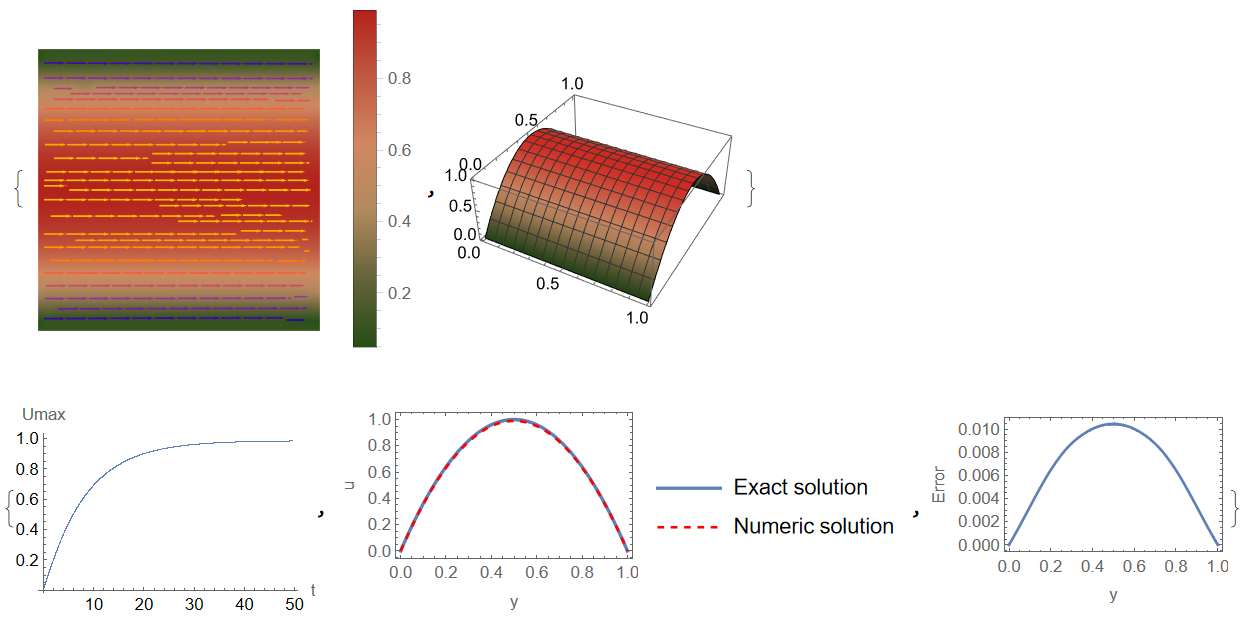
Actually for r=7 we have a good convergence to the exact solution on the grid of 12 points with error of $10^{−2}$. For r=5 the error is about 0.2 and for r=10 error is about $10^{−2}$, therefore r=7 is optimal value.
Update 2. In the module advect we can use trilinear interpolation as follows
advect[n_, d0_, u_, v_, w_, dt_] :=
Module[{x, y, z, d1, dt0, i0, i1, j0, j1, k0, k1, s0, s1, t0, t1,
p1, p0, d00, d10, d01, d11, cd0, cd1, xd, yd, zd},
d1 = ConstantArray[0, {n + 1, n + 1, n + 1}]; dt0 = dt n;
Do[Do[Do[x = i - dt0 u[[i, j, k]]; y = j - dt0 v[[i, j, k]];
z = k - dt0 w[[i, j, k]];
i0 = Which[x <= 1, 1, 1 < x < n, Floor[x], True, n];
i1 = i0 + 1;
j0 = Which[y <= 1, 1, 1 < y < n, Floor[y], True, n];
j1 = j0 + 1;
k0 = Which[z <= 1, 1, 1 < z < n, Floor[z], True, n];
k1 = k0 + 1;(*Trilinear interpolation*)xd = x - i0;
yd = y - j0; zd = z - k0;
d00 = d0[[i0, j0, k0]] (1 - xd) + d0[[i1, j0, k0]] xd;
d01 = d0[[i0, j0, k1]] (1 - xd) + d0[[i1, j0, k1]] xd;
d10 = d0[[i0, j1, k0]] (1 - xd) + d0[[i1, j1, k0]] xd;
d11 = d0[[i0, j1, k1]] (1 - xd) + d0[[i1, j1, k1]] xd;
cd0 = d00 (1 - yd) + d10 yd; cd1 = d01 (1 - yd) + d11 yd;
d1[[i, j, k]] = cd0 (1 - zd) + cd1 zd;
, {k, 2, n}];, {j, 2, n}];, {i, 1, n + 1}]; d1];
Update: testing projection step
To test projection step itself we can use Mathematica FEM and exact benchmark solution from well known paper EXACT FULLY 3D NAVIER-STOKES SOLUTIONS FOR BENCHMARKING by C. ROSS ETHIER AND D. A. STEINMAN as follows. First, we consider projection step as an implementation of the predictor-corrector algorithm $$\frac{u-u_n}{\tau}+(u.\nabla)u-\nu\nabla^2 u=0$$ $$\frac{u_{n+1}-u}{\tau}+\nabla p =0$$ here $\tau$ is time step, $u_n, u, u_{n+1}$ if velocity field on previous, intermediate and next step consequently, and $p$ is a pressure. We suppose that $\nabla.u_{n+1}=0$, and therefore $$\nabla^2p-\frac{\nabla.u}{\tau}=0$$ Second, we solve NSE in the unit cuboid with Dirichlet condition using exact solution and FEM, we have code
Clear["Global`*"]
Needs["NDSolve`FEM`"]
reg = Cuboid[];
mesh = ToElementMesh[reg, MaxCellMeasure -> 0.001];
(*Exact solution*)
U[x_, y_, z_,
t_] := -a Exp[-d^2 t] (Exp[a x] Sin[a y + d z] +
Exp[a z] Cos[a x + d y]);
V[x_, y_, z_,
t_] := -a Exp[-d^2 t] (Exp[a y] Sin[a z + d x] +
Exp[a x] Cos[a y + d z]);
W[x_, y_, z_,
t_] := -a Exp[-d^2 t] (Exp[a z] Sin[a x + d y] +
Exp[a y] Cos[a z + d x]);
P[x_, y_, z_,
t_] := -a ^2/
2 Exp[-2 d^2 t] (Exp[2 a x] + Exp[2 a y] + Exp[2 a z] +
2 Sin[a x + d y] Exp[a (y + z)] Cos[a z + d x] +
2 Sin[a y + d z] Exp[a (x + z)] Cos[a x + d y] +
2 Sin[a z + d x] Exp[a (y + x)] Cos[
a y + d z]);
(*t0 is time step, nn is number of iterations *)
a = 1; d = 1; t0 = 1/400; nn = 200; \[Nu] = 1;
(*FEM implementation of predictor-corrector algorithm*)
UX[0] = U[x, y, z, 0];
VY[0] = V[x, y, z, 0]; WZ[0] = W[x, y, z, 0];
P0[0] = P[x, y, z, 0];
Do[
{UX[i], VY[i], WZ[i], P0[i]} =
NDSolveValue[{{-\[Nu]*
Laplacian[
u[x, y, z], {x, y, z}] + (u[x, y, z] - UX[i - 1])/t0 +
UX[i - 1]*D[u[x, y, z], x] + VY[i - 1]*D[u[x, y, z], y] +
WZ[i - 1]*D[u[x, y, z], z], -\[Nu]*
Laplacian[
v[x, y, z], {x, y, z}] + (v[x, y, z] - VY[i - 1])/t0 +
UX[i - 1]*D[v[x, y, z], x] + VY[i - 1]*D[v[x, y, z], y] +
WZ[i - 1]*D[v[x, y, z], z], -\[Nu]*
Laplacian[
w[x, y, z], {x, y, z}] + (w[x, y, z] - WZ[i - 1])/t0 +
UX[i - 1]*D[w[x, y, z], x] + VY[i - 1]*D[w[x, y, z], y] +
WZ[i - 1]*D[w[x, y, z], z],
Laplacian[p[x, y, z], {x, y, z}] - (
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(w\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z])/t0} == {0, 0, 0, 0}, {
DirichletCondition[{u[x, y, z] ==
U[x, y, z, i t0 - t0/2] + t0 D[P[x, y, z, i t0], x],
v[x, y, z] ==
V[x, y, z, i t0 - t0/2] + t0 D[P[x, y, z, i t0], y],
w[x, y, z] ==
W[x, y, z, i t0 - t0/2] + t0 D[P[x, y, z, i t0], z],
p[x, y, z] == P[x, y, z, i t0 ]}, True]}}, {u[x, y, z] - t0
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], v[x, y, z] - t0
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], w[x, y, z] - t0
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z],
p[x, y, z]}, {x, y, z} \[Element] mesh,
Method -> {"FiniteElement",
"InterpolationOrder" -> {u -> 2, v -> 2, w -> 2,
p -> 2}}];, {i, 1, nn}];
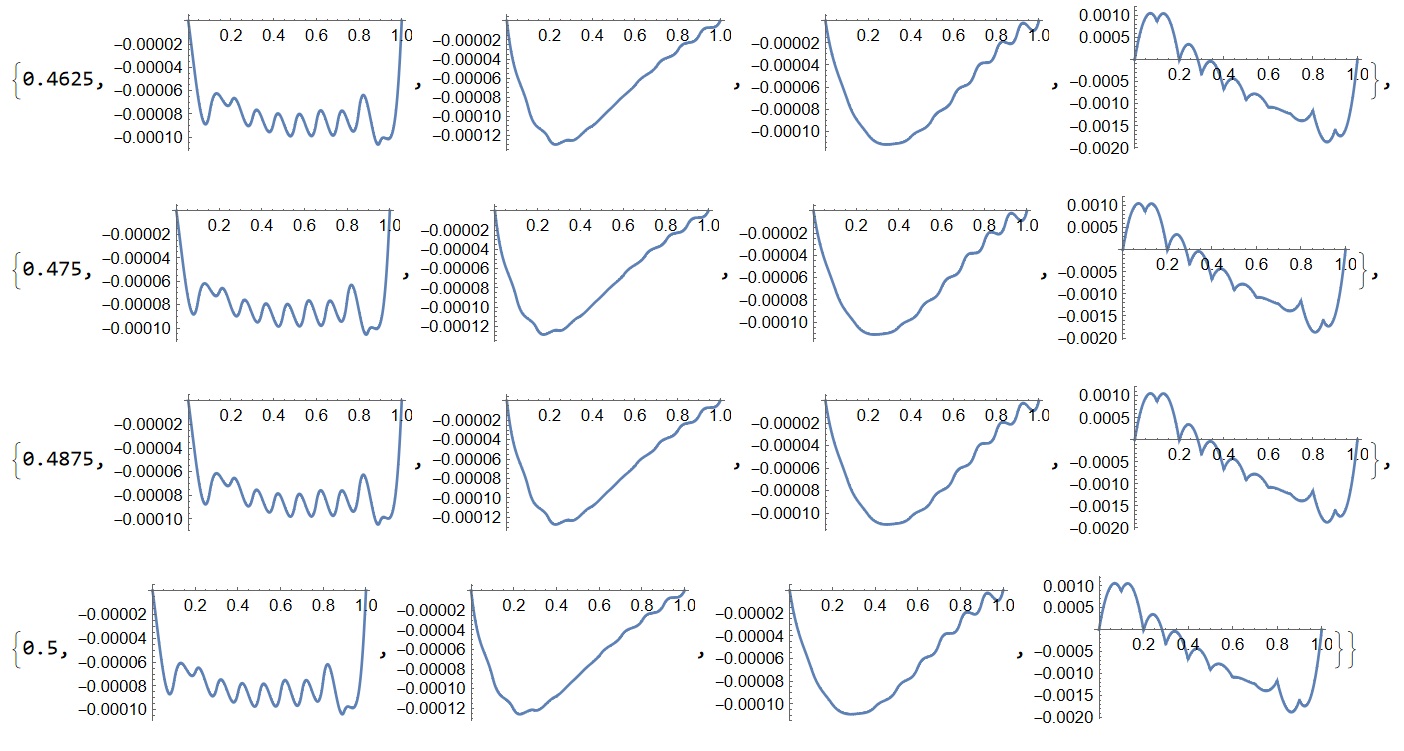
Visualization of error on every 5 steps on the line $x=1/2, z=1/2$ for $u_n=(UX[n],VY[n],WZ[n])$, and $p=P0[n]$
Table[{k t0 // N,
Plot[Evaluate[{U[x, y, z, k t0]/UX[k] - 1} /. {x -> 1/2,
z -> 1/2}], {y, 0, 1}, PlotRange -> All],
Plot[Evaluate[{V[x, y, z, k t0]/VY[k] - 1} /. {x -> 1/2,
z -> 1/2}], {y, 0, 1}, PlotRange -> All],
Plot[Evaluate[{W[x, y, z, k t0]/WZ[k] - 1} /. {x -> 1/2,
z -> 1/2}], {y, 0, 1}, PlotRange -> All],
Plot[Evaluate[{P[x, y, z, k t0]/P0[k] - 1} /. {x -> 1/2,
z -> 1/2}], {y, 0, 1}, PlotRange -> All]}, {k, 5, nn, 5}]
Please note, that in the picture shown last steps only. The relative error for pressure is about $3\times 10^{-3}$, and for velocity $1.25\times10^{-3}$ on the grid $10\times10\times 10$ on 200 steps in time with time step $\tau =1/400$. 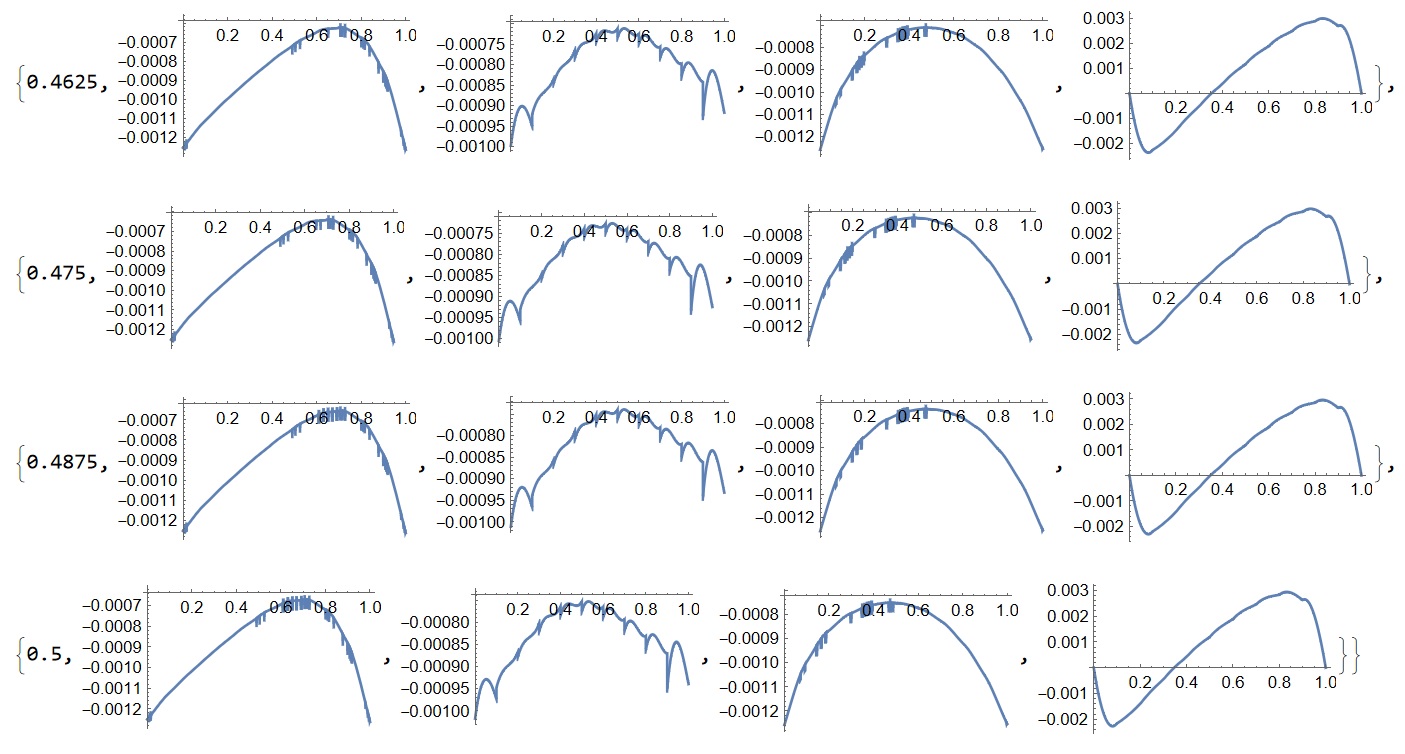
Using exact benchmark solution we also can test linear FEM algorithm described on Solver for unsteady flow with the use of Mathematica FEM and extended to 3D below as follows
Needs["NDSolve`FEM`"]
reg = Cuboid[];
mesh = ToElementMesh[reg, MaxCellMeasure -> 0.001]
U[x_, y_, z_,
t_] := -a Exp[-d^2 t] (Exp[a x] Sin[a y + d z] +
Exp[a z] Cos[a x + d y]);
V[x_, y_, z_,
t_] := -a Exp[-d^2 t] (Exp[a y] Sin[a z + d x] +
Exp[a x] Cos[a y + d z]);
W[x_, y_, z_,
t_] := -a Exp[-d^2 t] (Exp[a z] Sin[a x + d y] +
Exp[a y] Cos[a z + d x]);
P[x_, y_, z_,
t_] := -a ^2/
2 Exp[-2 d^2 t] (Exp[2 a x] + Exp[2 a y] + Exp[2 a z] +
2 Sin[a x + d y] Exp[a (y + z)] Cos[a z + d x] +
2 Sin[a y + d z] Exp[a (x + z)] Cos[a x + d y] +
2 Sin[a z + d x] Exp[a (y + x)] Cos[
a y + d z]); a = 1; d = 1; t0 = 1/400; nn = 200; \[Nu] = 1;
UX[0] = U[x, y, z, 0];
VY[0] = V[x, y, z, 0]; WZ[0] = W[x, y, z, 0];
P0[0] = P[x, y, z, 0];
Do[
{UX[i], VY[i], WZ[i], P0[i]} =
NDSolveValue[{{-\[Nu]*
Laplacian[
u[x, y, z], {x, y, z}] + (u[x, y, z] - UX[i - 1])/t0 +
UX[i - 1]*D[u[x, y, z], x] + VY[i - 1]*D[u[x, y, z], y] +
WZ[i - 1]*D[u[x, y, z], z] +
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], -\[Nu]*
Laplacian[
v[x, y, z], {x, y, z}] + (v[x, y, z] - VY[i - 1])/t0 +
UX[i - 1]*D[v[x, y, z], x] + VY[i - 1]*D[v[x, y, z], y] +
WZ[i - 1]*D[v[x, y, z], z] +
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], -\[Nu]*
Laplacian[
w[x, y, z], {x, y, z}] + (w[x, y, z] - WZ[i - 1])/t0 +
UX[i - 1]*D[w[x, y, z], x] + VY[i - 1]*D[w[x, y, z], y] +
WZ[i - 1]*D[w[x, y, z], z] +
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], (
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(w\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z])} == {0, 0, 0, 0}, {
DirichletCondition[{u[x, y, z] == U[x, y, z, i t0],
v[x, y, z] == V[x, y, z, i t0],
w[x, y, z] == W[x, y, z, i t0],
p[x, y, z] == P[x, y, z, i t0]}, True]}}, {u[x, y, z] ,
v[x, y, z] , w[x, y, z] , p[x, y, z]}, {x, y, z} \[Element]
mesh, Method -> {"FiniteElement",
"InterpolationOrder" -> {u -> 2, v -> 2, w -> 2,
p -> 1}}];, {i, 1, nn}];
Visualization of error on every 5 steps on the line $y=1/2,z=1/2$ for $u_n=(UX[n],VY[n],WZ[n])$, and $p=P0[n]$
Table[{k t0 // N,
Plot[Evaluate[{U[x, y, z, k t0]/UX[k] - 1} /. {y -> 1/2,
z -> 1/2}], {x, 0, 1}, PlotRange -> All],
Plot[Evaluate[{V[x, y, z, k t0]/VY[k] - 1} /. {y -> 1/2,
z -> 1/2}], {x, 0, 1}, PlotRange -> All],
Plot[Evaluate[{W[x, y, z, k t0]/WZ[k] - 1} /. {y -> 1/2,
z -> 1/2}], {x, 0, 1}, PlotRange -> All],
Plot[Evaluate[{P[x, y, z, k t0]/P0[k] - 1} /. {y -> 1/2,
z -> 1/2}], {x, 0, 1}, PlotRange -> All]}, {k, 5, nn, 5}]
Note, that in the picture shown last steps only. The relative error for pressure is about $2×10^{−3}$, and for velocity $1.5×10^{−4}$ on the grid 10×10×10 on 200 steps in time with time step τ=1/400.