I started the discussion here but I also want to repeat on this forum. There are many commercial and open code for solving the problems of unsteady flows. We are interested in the possibility of solving these problems using Mathematica FEM. Previously proposed solvers for stationary incompressible isothermal flows:
Solving 2D Incompressible Flows using Finite Elements: http://community.wolfram.com/groups/-/m/t/610335
FEM Solver for Navier-Stokes equations in 2D: http://community.wolfram.com/groups/-/m/t/611304
Nonlinear FEM Solver for Navier-Stokes equations in 2D: https://mathematica.stackexchange.com/questions/94914/nonlinear-fem-solver-for-navier-stokes-equations-in-2d/96579#96579
We give several examples of the successful application of the finite element method for solving unsteady problem including nonisothermal and compressible flows. We will begin with two standard tests that were proposed to solve this class of problems by
M. Schäfer and S. Turek, Benchmark computations of laminar ?ow around a cylinder (With support by F. Durst, E. Krause and R. Rannacher). In E. Hirschel, editor, Flow Simulation with High-Performance Computers II. DFG priority research program results 1993-1995, number 52 in Notes Numer. Fluid Mech., pp.547566. Vieweg, Weisbaden, 1996. https://www.uio.no/studier/emner/matnat/math/MEK4300/v14/undervisningsmateriale/schaeferturek1996.pdf
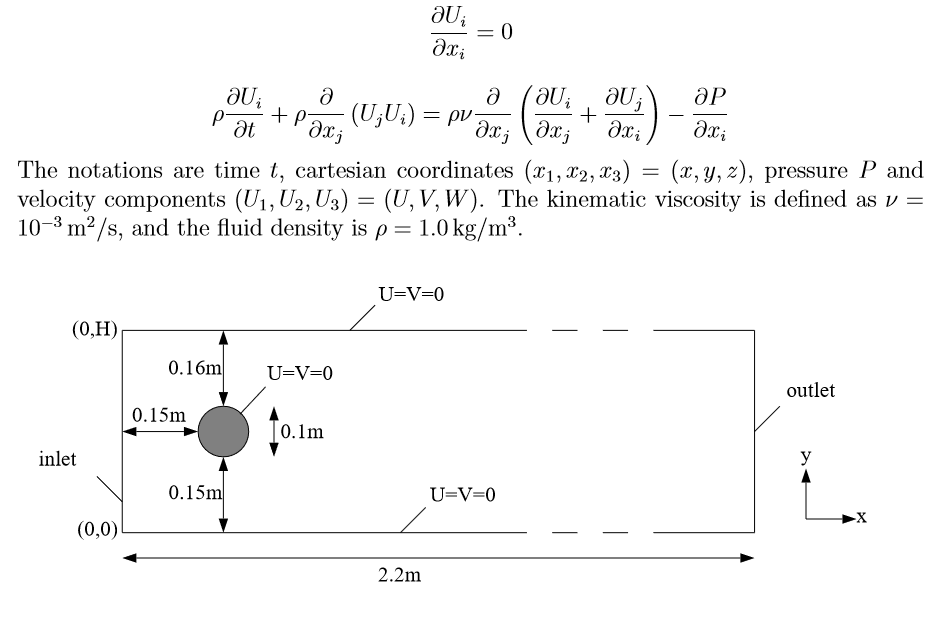
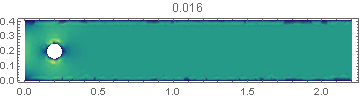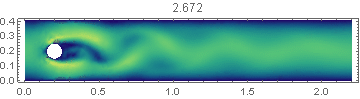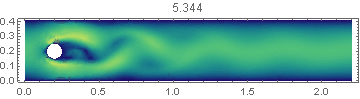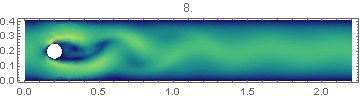
Let us consider the flow in a flat channel around a cylinder at Reynolds number = 100, when self-oscillations occur leading to the detachment of vortices in the aft part of cylinder. In this problem it is necessary to calculate drag coe?cient, lift coe?cient and pressure di?erence in the frontal and aft part of the cylinder as functions of time, maximum drag coe?cient, maximum lift coe?cient , Strouhal number and pressure di?erence $\Delta P(t)$ at $t = t0 +1/2f$. The frequency f is determined by the period of oscillations of lift coe?cient f=f(c_L). The data for this test, the code and the results are shown below.
H = .41; L = 2.2; {x0, y0, r0} = {1/5, 1/5, 1/20};
? = RegionDifference[Rectangle[{0, 0}, {L, H}], Disk[{x0, y0}, r0]];
RegionPlot[?, AspectRatio -> Automatic]
K = 2000; Um = 1.5; ? = 10^-3; t0 = .004;
U0[y_, t_] := 4*Um*y/H*(1 - y/H)
UX[0][x_, y_] := 0;
VY[0][x_, y_] := 0;
P0[0][x_, y_] := 0;
Do[
{UX[i], VY[i], P0[i]} =
NDSolveValue[{{Inactive[
Div][({{-?, 0}, {0, -?}}.Inactive[Grad][
u[x, y], {x, y}]), {x, y}] +
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + (u[x, y] - UX[i - 1][x, y])/t0 +
UX[i - 1][x, y]*D[u[x, y], x] +
VY[i - 1][x, y]*D[u[x, y], y],
Inactive[
Div][({{-?, 0}, {0, -?}}.Inactive[Grad][
v[x, y], {x, y}]), {x, y}] +
\!\(\*SuperscriptBox[\(p\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + (v[x, y] - VY[i - 1][x, y])/t0 +
UX[i - 1][x, y]*D[v[x, y], x] +
VY[i - 1][x, y]*D[v[x, y], y],
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] +
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y]} == {0, 0, 0} /. ? -> ?, {
DirichletCondition[{u[x, y] == U0[y, i*t0], v[x, y] == 0},
x == 0.],
DirichletCondition[{u[x, y] == 0., v[x, y] == 0.},
0 <= x <= L && y == 0 || y == H],
DirichletCondition[{u[x, y] == 0,
v[x, y] == 0}, (x - x0)^2 + (y - y0)^2 == r0^2],
DirichletCondition[p[x, y] == P0[i - 1][x, y], x == L]}}, {u, v,
p}, {x, y} ? ?,
Method -> {"FiniteElement",
"InterpolationOrder" -> {u -> 2, v -> 2, p -> 1},
"MeshOptions" -> {"MaxCellMeasure" -> 0.001}}], {i, 1, K}];
{ContourPlot[UX[K/2][x, y], {x, y} ? ?,
AspectRatio -> Automatic, ColorFunction -> "BlueGreenYellow",
FrameLabel -> {x, y}, PlotLegends -> Automatic, Contours -> 20,
PlotPoints -> 25, PlotLabel -> u, MaxRecursion -> 2],
ContourPlot[VY[K/2][x, y], {x, y} ? ?,
AspectRatio -> Automatic, ColorFunction -> "BlueGreenYellow",
FrameLabel -> {x, y}, PlotLegends -> Automatic, Contours -> 20,
PlotPoints -> 25, PlotLabel -> v, MaxRecursion -> 2,
PlotRange -> All]} // Quiet
{DensityPlot[UX[K][x, y], {x, y} ? ?,
AspectRatio -> Automatic, ColorFunction -> "BlueGreenYellow",
FrameLabel -> {x, y}, PlotLegends -> Automatic, PlotPoints -> 25,
PlotLabel -> u, MaxRecursion -> 2],
DensityPlot[VY[K][x, y], {x, y} ? ?,
AspectRatio -> Automatic, ColorFunction -> "BlueGreenYellow",
FrameLabel -> {x, y}, PlotLegends -> Automatic, PlotPoints -> 25,
PlotLabel -> v, MaxRecursion -> 2, PlotRange -> All]} // Quiet
dPl = Interpolation[
Table[{i*t0, (P0[i][.15, .2] - P0[i][.25, .2])}, {i, 0, K, 1}]];
cD = Table[{t0*i, NIntegrate[(-?*(-Sin[?] (Sin[?]
\!\(\*SuperscriptBox[\(UX[i]\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]] + Cos[?]
\!\(\*SuperscriptBox[\(UX[i]\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]]) + Cos[?] (Sin[?]
\!\(\*SuperscriptBox[\(VY[i]\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]] + Cos[?]
\!\(\*SuperscriptBox[\(VY[i]\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]]))*Sin[?] -
P0[i][x0 + r Cos[?], y0 + r Sin[?]]*
Cos[?]) /. {r -> r0}, {?, 0, 2*Pi}]}, {i,
1000, 2000}]; // Quiet
cL = Table[{t0*i, -NIntegrate[(-?*(-Sin[?] (Sin[?]
\!\(\*SuperscriptBox[\(UX[i]\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]] + Cos[?]
\!\(\*SuperscriptBox[\(UX[i]\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]]) +
Cos[?] (Sin[?]
\!\(\*SuperscriptBox[\(VY[i]\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]] + Cos[?]
\!\(\*SuperscriptBox[\(VY[i]\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x0 + r Cos[?],
y0 + r Sin[?]]))*Cos[?] +
P0[i][x0 + r Cos[?], y0 + r Sin[?]]*
Sin[?]) /. {r -> r0}, {?, 0, 2*Pi}]}, {i,
1000, 2000}]; // Quiet
{ListLinePlot[cD,
AxesLabel -> {"t", "\!\(\*SubscriptBox[\(c\), \(D\)]\)"}],
ListLinePlot[cL,
AxesLabel -> {"t", "\!\(\*SubscriptBox[\(c\), \(L\)]\)"}],
Plot[dPl[x], {x, 0, 8}, AxesLabel -> {"t", "?P"}]}
f002 = FindFit[cL, a*.5 + b*.8*Sin[k*16*t + c*1.], {a, b, k, c}, t]
Plot[Evaluate[a*.5 + b*.8*Sin[k*16*t + c*1.] /. f002], {t, 4, 8},
Epilog -> Map[Point, cL]]
k0=k/.f002;
Struhalnumber = .1*16*k0/2/Pi
cLm = MaximalBy[cL, Last]
sol = {Max[cD[[All, 2]]], Max[cL[[All, 2]]], Struhalnumber,
dPl[cLm[[1, 1]] + Pi/(16*k0)]}
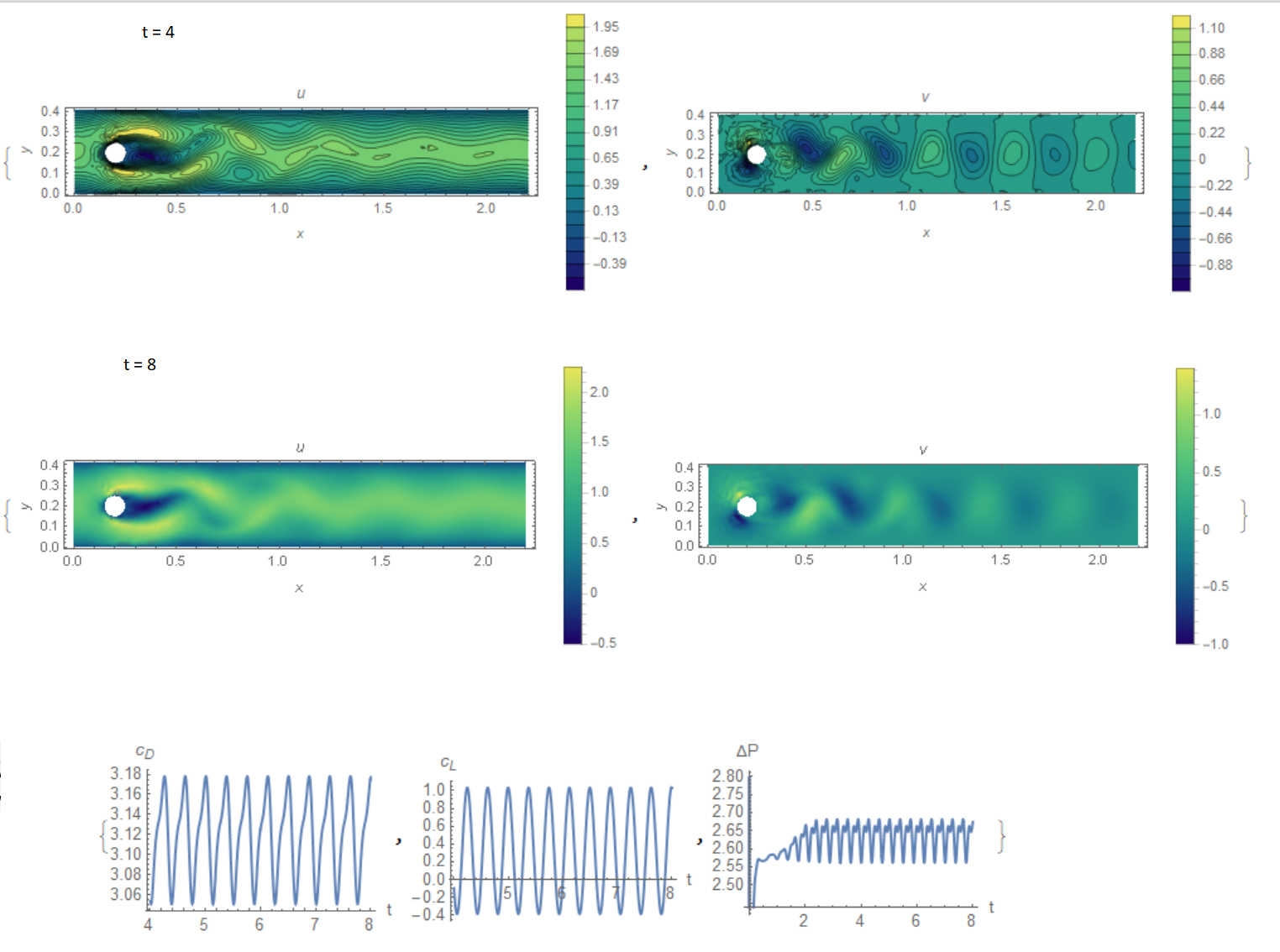
In Fig. 1 shows the components of the flow velocity and the required coefficients. Our solution of the problem and what is required in the test
{3.17805, 1.03297, 0.266606, 2.60427}
lowerbound= { 3.2200, 0.9900, 0.2950, 2.4600};
upperbound = {3.2400, 1.0100, 0.3050, 2.5000};
 Note that our results differ from allowable by several percent, but if you look at all the results of Table 4 from the cited article, then the agreement is quite acceptable.The worst prediction is for the Strouhal number. We note that we use the explicit Euler method, which gives an underestimate of the Strouhal number, as follows from the data in Table 4.
Note that our results differ from allowable by several percent, but if you look at all the results of Table 4 from the cited article, then the agreement is quite acceptable.The worst prediction is for the Strouhal number. We note that we use the explicit Euler method, which gives an underestimate of the Strouhal number, as follows from the data in Table 4.
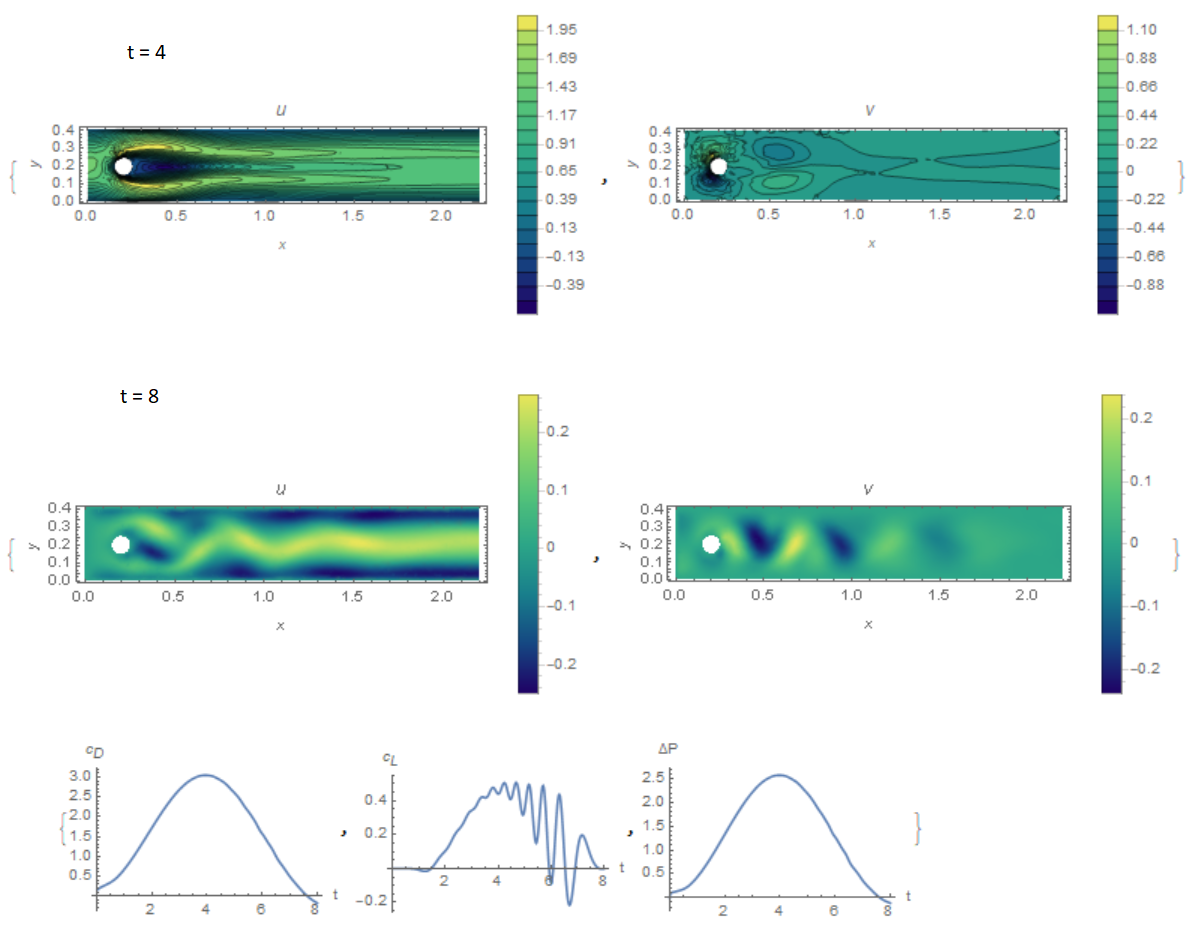
The next test differs from the previous one in that the input speed varies according to the U0[y_, t_] := 4*Um*y/H*(1 - y/H)*Sin[Pi*t/8]. It is necessary to determine the time dependence of the drag and lift parameters for a half-period of oscillation, as well as the pressure drop at the last moment of time. In Fig. 2 shows the components of the flow velocity and the required coefficients. Our solution of the problem and what is required in the test
sol = {3.0438934441256595`,
0.5073345082785012`, -0.11152933279750943`};
lowerbound = {2.9300, 0.4700, -0.1150};
upperbound = {2.9700, 0.4900, -0.1050};
 For this test, the agreement with the data in Table 5 is good. Consequently, the two tests are almost completely passed. I wrote and debugged this code using Mathematics 11.01. But when I ran this code using Mathematics 11.3, I got strange pictures, for example, the disk is represented as a hexagon, the size of the area is changed.
For this test, the agreement with the data in Table 5 is good. Consequently, the two tests are almost completely passed. I wrote and debugged this code using Mathematics 11.01. But when I ran this code using Mathematics 11.3, I got strange pictures, for example, the disk is represented as a hexagon, the size of the area is changed. 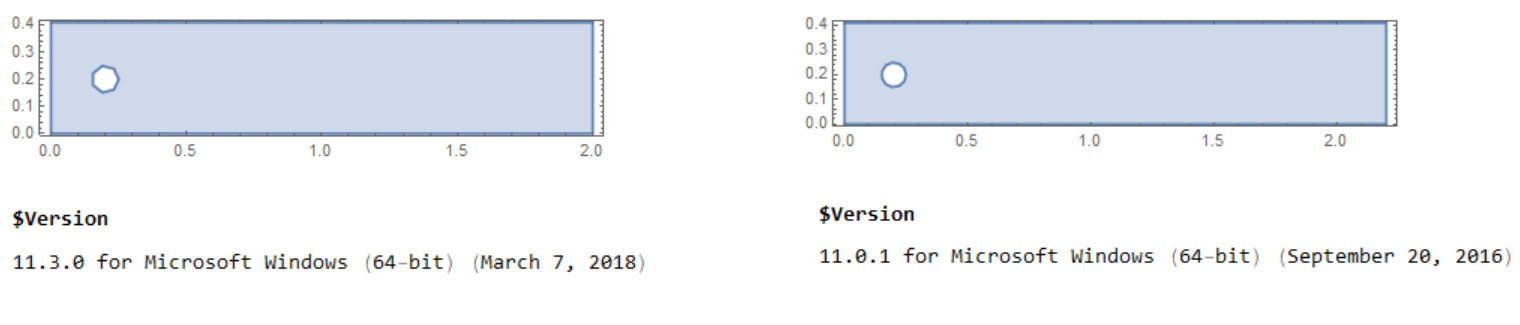 In addition, the numerical solution of the problem has changed, for example, test 2D2
In addition, the numerical solution of the problem has changed, for example, test 2D2
{3.17805, 1.03297, 0.266606, 2.60427} v11.01
{3.15711, 1.11377, 0.266043, 2.54356} v11.03
The attached file contains the working code for test 2D3 describing the flow around the cylinder in a flat channel with a change in the flow velocity.
 Attachments:
Attachments: