Recently I have been doing a lot of double and triple integrals. To my disappointment, Mathematica does not have built-in integral signs for those advanced or special integrals. Fortunately, I have found out a way to introduce those integral signs from Unicode. In Mathematica, it can be input by typing the "\:unicode number "of the integral sign.
But a new problem emerged after the introduction: when converting expressions containing my self-introduced integral signs into Latex code, Mathematica will multiply the integral sign into the numerator as long as the integrand is a fractional function.
For example, I have this expression input in my note book:
\!\(\*UnderscriptBox[
StyleBox["∬",
FontSize->24], \(1 <=
\*SuperscriptBox[\(x\), \(2\)] +
\*SuperscriptBox[\(y\), \(2\)] <= 4\)]\) Sin[\[Pi] Sqrt[
x^2 + y^2]]/Sqrt[x^2 + y^2] \[DifferentialD]x \[DifferentialD]y
which looks like :
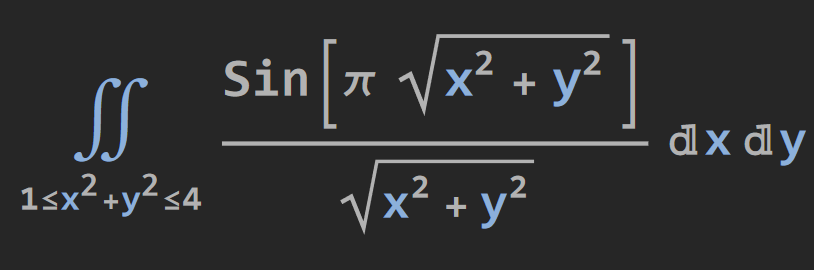
However, the latex code Mathematica made for this expression is:
$$ \frac{\iint\limits_{1\leq x^2+y^2\leq 4}\sin \left(\pi \sqrt{x^2+y^2}\right)\mathrm{d}x\mathrm{d}y}{\sqrt{x^2+y^2}} $$
where apparently Mathematica regards my self-introduced integral sign as an ordinary term which can be multiplied into the numerator. But unfortunately, it can't. By doing so the meaning and value of the expression has totally changed from the correct one.
Moreover, I have noticed that, for built-in integral signs, Mathematica will interpret the integral expression properly and will not multiply those integral signs into the numerator, which shows there must be some way to pull it off.
I already know that to convert an expression into its TexForm, Mathematica will work on its Box representation of its traditional form. As a result, I was wondering, how I can prevent my self-introduced integral sign being multiplied into the numerator when converting it into Latex code, or more specifically, preventing so when the expression's Box representation of its traditional form is being made by Mathematica.