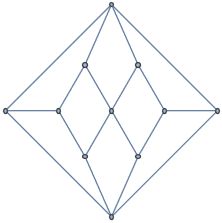
The Herschel graph is smallest smallest nonhamiltonian polyhedral graph.
GraphData["HerschelGraph"]
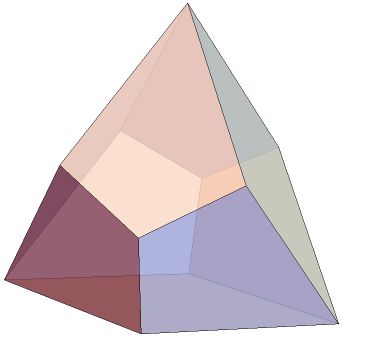
I've pondered how to improve my Canonical Polyhedra demo / function to give exact values. A polyhedron is canonical if it has a unit midsphere tangent to all edges. Here's exact values for a canonical Herschel ennehedron:
herschel=Polyhedron[With[{a=1/8 Sqrt[1/2 (5+3 Sqrt[17])], b=1/8 Sqrt[3/2 (23+Sqrt[17])]},
{{0,-b,-2a},{2Sqrt[3]a,0,-2a},{0,b,-2a},{-2Sqrt[3]a,0,-2a},{0,-4/3 b,0},{0,4/3 b,0},{Sqrt[3]a,-b,a},
{Sqrt[3]a,b,a},{-Sqrt[3]a,-b,a},{-Sqrt[3]a,b,a},{0,0,4a}}], {{1,2,3,4},{1,4,9,5},{1,5,7,2},{2,7,11,8},
{2,8,6,3},{3,6,10,4},{4,10,11,9},{5,9,11,7},{6,8,11,10}}];
It's a nice looking poly.
Looking at it, I wondered how 4 of them would fit together.
Graphics3D[{Opacity[.8],herschel,ResourceFunction["PolyhedronFaceReflect"][herschel,2],ResourceFunction["PolyhedronFaceReflect"][herschel,3],ResourceFunction["PolyhedronFaceReflect"][herschel,8]},Boxed->False]
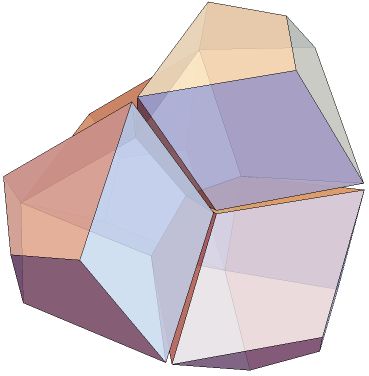
Not quite a fit. However, if the requirement for a midsphere was dropped, it seems this shape could be tweaked to work nicely with a rhombic dodecahedron.
Update
Here's the "simpler" form that might work with the rhombic dodecahedron:
points = {{0, 0, 0}, {12, 0, 0}, {0, 0, 12}, {0, 12, 0}, {3, 3, -3}, {3, -3, 3}, {-3, 3, 3}, {9, 9, 3}, {9, 3, 9}, {3, 9, 9}, {8, 8, 8}}/6;
ConvexHullMesh[points]
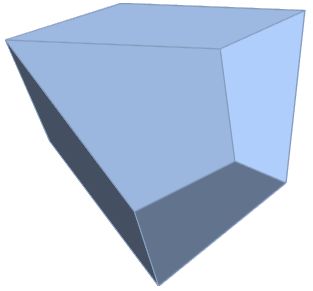
This could work with the following dodecahedron:
Select[Tuples[Range[-2,2],{3}], MemberQ[{{1,1,1},{0,0,2}},Sort[Abs[#]]]&]
Update 2: It doesn't work. The diamond doesn't match up.
 Attachments:
Attachments: