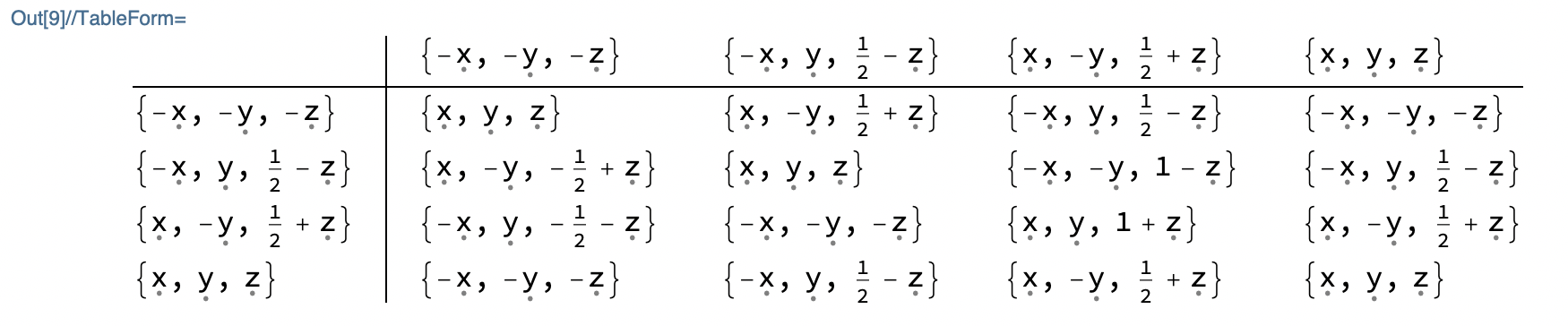It's amazing where our thoughts come from. As from out of the blue while reading a book about a beech wood in England I realized that both myself and Danny overlooked that fact that the space groups are infinite groups. And because they are infinite, so are their multiplication tables.

Including the generators {1, 0, 0}, {0, 1, 0}, and {0, 0, 1} are necessary to form the full group.

My code generates the group elements modulo 1 to keep all the products within the unit cell.

A PDF version of the International Tables is available. The Pcc2 example is on pp. 222-223.

This is the code I use:

Options[symmDot] = {Variables -> {\[FormalX], \[FormalY], \[FormalZ]}}; 

symmDot[s1_List, sn___List, opts : OptionsPattern[]] /; 
  		MatchQ[Dimensions[{s1, sn}], {_, 1 | 2 | 3}] := 
 	Fold[sd[##1, opts] & , s1, {sn}]

sd[s1_, s2_, OptionsPattern[symmDot]] := 
 	s2 /. Thread[Take[OptionValue[Variables], Length[s1]] -> s1]

(s1_List) \[CircleDot] (sn___List) := symmDot[s1, sn]

generateGroup[generators : {{__} ..}, times_ : symmDot] /; 
  		MatchQ[Dimensions[generators], {_, 1 | 2 | 3}] := 
 	Module[{group = generators, new}, 
  		While[
   			MatchQ[
    				new = Complement[
      					Apply[Join, {Outer[times, group, generators, 1], 
         						Outer[times, generators, group, 1]}, {0, 1}] /. 
       							Plus[n : (_Integer | _Rational), a__] :> 
        								Plus[Mod[n, 1], a], 
      					group](* // Echo[#, "|new| ", Length@#&]&*), 
    				{__}], 
   			group = Join[group, new](* // Echo[#, "|group| ", Length]&*)
   			]; 
  		Sort @ group
  		]

I use formal symbols, such as \[FormalX], so that they are guaranteed to be without a value.

Taking the space group Pcc2 (No. 27) as an example, there are two generators:

In[7]:= elements = generateGroup[{{-\[FormalX], -\[FormalY], -\[FormalZ]}, 
   {\[FormalX], -\[FormalY], \[FormalZ] + 1/2}}]

Out[7]= {{-\[FormalX], -\[FormalY], -\[FormalZ]}, {-\[FormalX], \[FormalY], 
  1/2 - \[FormalZ]}, {\[FormalX], -\[FormalY], 
  1/2 + \[FormalZ]}, {\[FormalX], \[FormalY], \[FormalZ]}}

The multiplication table can be generated with Outer:

In[8]:= mulTable = Outer[symmDot, elements, elements, 1]

Out[8]= {{{\[FormalX], \[FormalY], \[FormalZ]}, {\[FormalX], -\
\[FormalY], 1/2 + \[FormalZ]}, {-\[FormalX], \[FormalY], 
   1/2 - \[FormalZ]}, {-\[FormalX], -\[FormalY], -\[FormalZ]}}, {{\
\[FormalX], -\[FormalY], -(1/
     2) + \[FormalZ]}, {\[FormalX], \[FormalY], \[FormalZ]}, {-\
\[FormalX], -\[FormalY], 1 - \[FormalZ]}, {-\[FormalX], \[FormalY], 
   1/2 - \[FormalZ]}}, {{-\[FormalX], \[FormalY], -(1/
     2) - \[FormalZ]}, {-\[FormalX], -\[FormalY], -\[FormalZ]}, {\
\[FormalX], \[FormalY], 1 + \[FormalZ]}, {\[FormalX], -\[FormalY], 
   1/2 + \[FormalZ]}}, {{-\[FormalX], -\[FormalY], -\[FormalZ]}, {-\
\[FormalX], \[FormalY], 1/2 - \[FormalZ]}, {\[FormalX], -\[FormalY], 
   1/2 + \[FormalZ]}, {\[FormalX], \[FormalY], \[FormalZ]}}}

And displayed with TableForm:

TableForm[mulTable, TableHeadings -> {elements, elements}, 
 TableDepth -> 2]

I basically solved this problem by applying all the group elements to a particular coordinate, such as {0,0,0}, and then analyzing the lattice corresponding to the resulting vector set, say, by LatticeReduce.

@Daniel Lichtblau

I didn't use a matrix representation. It's what I would use if this were my problem to tackle.

Thank you for your confirmation. I got your idea. You mean that for a real problem, the matrix representation will be used. This is also what I would do, and also the final solution to any practical problem.