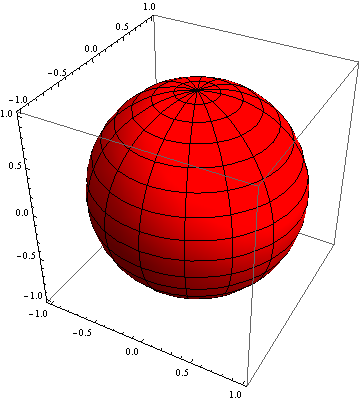
White is the middle of the range for the default ColorFunction -> Automatic (that becomes ColorData["LightTemperatureMap"]). K for this sphere will be 1 everywhere.
In[ ]:= GaussianCurvature[{Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]}, {u, v}]
Out[ ]= 1
GaussianCurvature of this sphere in Plot3D gives PlotRange of {0., 2.} when rescaled, the curvature becomes 0.5 and "LightTemperatureMap" makes white.
In[ ]:= ColorData["LightTemperatureMap"][Rescale[1, {0., 2.}]]
Out[ ]= RGBColor[0.931655, 0.995208, 0.909049]
Replace the default ColorFunction with one you design and remove the Rescale step.
GaussianCurvature[f_, {u_, v_}] :=
Simplify[(Det[{D[f, {u, 2}], D[f, u], D[f, v]}] Det[{D[f, {v, 2}],
D[f, u], D[f, v]}] -
Det[{D[f, u, v], D[f, u],
D[f, v]}]^2)/(D[f, u].D[f, u] D[f, v].D[f,
v] - (D[f, u].D[f, v])^2)^2];
Options[gccolor] =
Select[Options[ParametricPlot3D], FreeQ[#, ColorFunctionScaling] &];
Off[RuleDelayed::rhs];
signgccolor[f_, {u_, ura__}, {v_, vra__}, opts___?OptionQ] :=
Module[{cf, gc, rng},
cf = ColorFunction /. {opts} /. Options[gccolor];
If[cf === Automatic, cf = (Which[
Positive[#], RGBColor[1, 0, 0],
Negative[#], RGBColor[0, 0, 1],
True, RGBColor[1, 1, 1]] &)];
gc[u_, v_] = GaussianCurvature[f, {u, v}];
(*rng=Last[PlotRange/.AbsoluteOptions[Plot3D[gc[u,v],{u,ura},{v,
vra},PerformanceGoal\[Rule]"Speed",PlotRange\[Rule]Full],
PlotRange]];*)
ParametricPlot3D[f, {u, ura}, {v, vra},
ColorFunction -> Function[{x, y, z, u, v}, cf[gc[u, v]]],
ColorFunctionScaling -> False,
Evaluate[FilterRules[{opts}, Options[gccolor]]]]];
On[RuleDelayed::rhs];
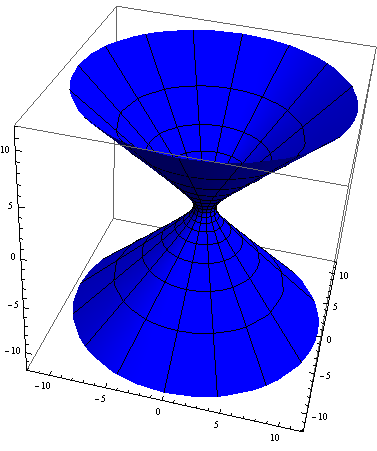
test hyperboloid, a surface of negative Gaussian curvature
signgccolor[{Cos[u] Cosh[v], Sin[u] Cosh[v], Sinh[v]}, {u, 0, 2 Pi}, {v, -Pi, Pi}]
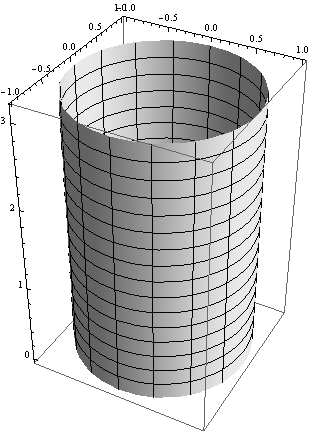
test cylinder, a surface of zero Gaussian curvature
signgccolor[{Cos[u], Sin[u], v}, {u, 0, 2 Pi}, {v, 0, Pi}]
test sphere, a surface of positive Gaussian curvature
signgccolor[{Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]}, {u, 0, 2 Pi}, {v, 0, Pi}]