Message Boards Message Boards

Analyzing a competitive new method for GenerateTiling

Brad Klee, Wolfram Research
Posted 2 years ago

Previous timing tests (here and here) made it seem likely that template tilings as computable by GenerateTiling could possibly be enumerated more rapidly by a home brewed algorithm. The underlying reason is that SatsifiabilityInstances is designed for a special class of boolean functions (using only And, Or, Not); whereas, the template tiling problem is really just an exact cover problem. It turns out that our developing intuition on this question is probably correct. The purpose of this memo is to show base case evidence, which looks very promising with regard to a competitive new method for GenerateTiling (and other related search functions).

In fact, the first attempt was a total failure, where pre-existing code even outpaced construction of the basic data for the exact cover problem. We then went back to the drawing board to find a much simpler schema, which is easy to understand and easy to compute on. The schema is computed by two functions only: 

PadTemplate[template_, size_] := 
 With[{colLen = size[[2]] + Dimensions[template][[2]] - 1},
  Join[PadRight[#, colLen, _] & /@ template, 
   Table[ConstantArray[_, colLen], {size[[1]] - 1}]]]

AllTemplates[template_, size_] := With[{
   padded = PadTemplate[template, size]},
  Catenate@Outer[Function[{row, col},
     RotateRight[RotateRight[#, col] & /@ padded, row
       ][[-size[[1]] ;; -1, -size[[2]] ;; -1]]],
    Range[0, size[[1]] + Dimensions[template][[1]] - 2],
    Range[0, size[[2]] + Dimensions[template][[2]] - 2],
    1]]

And computations are done using only two or three functions:

EitherMatchQ[a_, b_] := Or[MatchQ[a, b], MatchQ[b, a]]

RowsCombine[row1_, row2_] := Catch[MapThread[If[EitherMatchQ[#1, #2],
     First[Sort[{#1, #2}]], Throw[Nothing] ] &, {row1, row2}]]

GenerateBinaryCover[templates_, size_Integer] := 
 GenerateBinaryCover[templates, {size, size}]

GenerateBinaryCover[templates_, size_] := Fold[
  Union@Catenate[Outer[RowsCombine, #1, #2, 1]] &, {Table[_, 
    Times @@ size]},
  Transpose[(Catenate /@ AllTemplates[#, size]) & /@ templates ]]

The basic use case is: 

AbsoluteTiming[
 Length@ResourceFunction["GenerateTiling"][{IdentityMatrix[2], 
    Reverse[IdentityMatrix[2]]}, {}, 10, All]]

Out[]= {0.170944, 2}

AbsoluteTiming[
 Length@GenerateBinaryCover[{IdentityMatrix[2], 
    Reverse[IdentityMatrix[2]]}, 10]]

Out[]= {0.073363, 2}

From what I could read, this isn't written in the documentation, but setting "All" disables the fast SAT solver. In subsequent tests, we need to gauge comprehensive GenerateBinaryCover against GenerateTiling when it looks for only one result. In that case, the SAT solver wins the timing test above, because there is an easy answer to be found. In general, if there is no solution, the SAT solver still has to traverse an entire search tree, so does not necessarily improve its time over setting "All".

We will generate all binary $2 \times 2$ templates, and recursively test whether or not finite subsets lead successfully to a tiling of a $3\times3$ space. Level one only leads to monotonic, all black or all white tilings. The corresponding all-black and all-white templates can be filtered out of the set of sixteen, to obtain inputs for subsequent levels of the search: 

templates2 =   Partition[IntegerDigits[#, 2, 4], 2] & /@ Range[1, 2^4 - 2];
Grid[Partition[ArrayPlot[#, ImageSize -> 50] & /@ templates2, 7], 
 Spacings -> {1, 1}]

templates

data1 = Length@GenerateBinaryCover[#, 3] & /@ Subsets[templates2, {2}];
data2 = Replace[
     ResourceFunction["GenerateTiling"][#, {}, 3, 
      All], {_Failure -> 0, x_List :> Length[x]}] & /@ 
   Subsets[templates2, {2}];
SameQ[data1, data2]
Flatten[Position[data1, 2]]
Out[] = True
Out[] = {34, 51, 58}

The positions tell us which pairs of templates lead to periodic patterns. These can be filtered out when going to level 3, but first we need to check times: 

times1 =   AbsoluteTiming[GenerateBinaryCover[#, 3];][[1]] & /@ 
   Subsets[templates2, {2}];
times2 =   AbsoluteTiming[
      ResourceFunction["GenerateTiling"][#, {}, 3];][[1]] & /@ 
   Subsets[templates2, {2}];

Total[times1]
Total[times2]

Out[] = 0.068119
Out[] = 0.134045

It's only a factor of two overall, but we're testing a relatively naive and comprehensive Fold-based searcher against a solver, which we assume to be compiled and optimized by capable computer scientists. In that case, a factor of two sounds pretty good. Let's look more closely at the timing data: 

ListPlot[{times2, times1},
 PlotStyle -> {Red, Darker@Green},
 PlotRange -> All]

level 2 times

Notice three spikes on the green data (for GenerateBinaryCover) where the searcher is finding more than one viable tiling. These spikes could probably be removed by depth first searching, and perhaps an optimized depth-first search would increase the timing gap to a reliable order of magnitude.

At level three we find four more positive results: 

templates34Sub = Select[Subsets[templates2, {3}], 
  And @@ Function[{set}, ! 
         SubsetQ[set, Subsets[templates2, {2}][[#]]] & /@ {34, 51, 
        58}][#] &]

data1 = Length@Union@GenerateBinaryCover[#, 3] & /@ templates34Sub;
data2 = Replace[
     ResourceFunction["GenerateTiling"][#, {}, 3, 
      All], {_Failure -> 0, x_List :> Length[x]}] & /@ 
   templates34Sub;
SameQ[data1, data2]
Position[data1, x_Integer /; x > 0]

Out[] = True
Out[] = {{42}, {90}, {268}, {283}}

And the timing comparison is:

times13 =   AbsoluteTiming[GenerateBinaryCover[#, 3];][[1]] & /@ 
   templates34Sub;
times23 =   AbsoluteTiming[
      ResourceFunction["GenerateTiling"][#, {}, 3];][[1]] & /@ 
   templates34Sub;

ListPlot[{times13, times23},
 PlotStyle -> {Darker@Green, Red},
 PlotRange -> All]

L3 res

Similarly for levels 4 & 5:

l4 times

l 5 times

At level five total time is a draw due to increasing variance of the green data set, why? The variance is about a factor of eight, and eight is also the number of equivalent tilings found when a set is capable of tiling. So the variance can probably be blamed on the fact that GenerateBinaryCover is not designed for depth-first searching.

Although the timing stats above show a clear but narrow win for our simlpe algorithm, more work remains to be done improving the search recursion. More testing needs to be done to see if the ExactCover method scales as well as that SAT solver, maybe not.

POSTED BY: Brad Klee
2 Replies
Sort By:

Hey, thanks for the award! But perhaps we're moving too fast? The previous code doesn't do depth-first searching, and we haven't even solve the eight queens puzzle yet! Let's keep going on this one...

There is a BacktrackSearch available through WFR, but it seems to have a design flaw. Summer school students: Anyone can tell what is the flaw? If not, try comparing with this modified version of the source code, not too different really: 

BacktrackSearch[init_, levelData_, stateUpdate_,
  solutionQ_, max : (_Integer?Positive | All) : 1] := Module[{
   state = {init}, nextState, depth = Length[levelData], res = {},
   index, level = 1, solution, count = max},
  index = ConstantArray[0, {depth}];
  While[level > 0,
   nextState = Nothing;
   While[SameQ[nextState, Nothing] && (
      index[[level]] < Length[levelData[[level]]]),
    index[[level]]++;
    nextState = stateUpdate[Last[state],
      levelData[[level, index[[level]]]] ];];
   If[SameQ[nextState, Nothing],
    state = state[[1 ;; -2]]; index[[level--]] = 0,
    AppendTo[state, nextState]; level++];
   If[level > depth,
    If[solutionQ[Last[state]],
     If[max === 1,
       res = state;
       level = 0,
       AppendTo[res, state];
       If[--count == 0, level = 0];
       ];];
    state = state[[1 ;; -2]]; level--]
   ]; res]

Except that it now uses a stateUpdate function to compute partial solutions along the way. How does such an innovation improve timing statistics?

And for sake of reference, here's another similar Backtrack search function (of our own design):

DepthFirstIterate[stateUpdate_, solutionQ_,
   levelData_, levelLens_, maxLevel_, count_
   ][state_, inds_, level_] := Module[
  {nextState, res = Nothing, allRes = {},
   ind = 1, len = levelLens[[level]]},
  If[level == maxLevel + 1,
   If[solutionQ[Last[state]],
    Return[{state}], Return[{Nothing}]]];
  While[ind <= len,
   nextState = stateUpdate[Last[state], levelData[[level, ind]] ];
   If[SameQ[Nothing, nextState], ind++,
    res = DepthFirstIterate[stateUpdate, solutionQ,
       levelData, levelLens, maxLevel, count - Length[allRes]][
      Append[state, nextState], Append[inds, ind], level + 1];
    allRes = Join[allRes, res];
    If[Length[allRes] == count, Break[]];
    ind++]]; allRes]

DepthFirstSearch[init_, levelData_, stateUpdate_,
  solutionQ_, count : (_Integer?Positive | All) : 1] := Block[
  {$RecursionLimit = Infinity}, With[{
    levelLens = Append[Length /@ levelData, 0],
    depth = Length@levelData},
   If[SameQ[Length[#], count, 1],
      First[#], #] &[
    DepthFirstIterate[
      stateUpdate, solutionQ,
      levelData, levelLens, depth, count
      ][{init}, {}, 1]]]]

Now we actually have not one, but three possible methods for GenerateTiling. For the sake of clarity we will put the new methods into another function GenerateCover and wrap that with GenerateTemplatePattern: 

PadTemplate[template_, size_] := With[
  {colLen = size[[2]] + Dimensions[template][[2]] - 1},
  Join[PadRight[#, colLen, _] & /@ template, 
   Table[ConstantArray[_, colLen], {size[[1]] - 1}]]]

AllTemplates[template_, size_] := With[{
   padded = PadTemplate[template, size]},
  Catenate@Outer[Function[{row, col},
     RotateRight[RotateRight[#, col] & /@ padded, row
       ][[-size[[1]] ;; -1, -size[[2]] ;; -1]]],
    Range[0, size[[1]] + Dimensions[template][[1]] - 2],
    Range[0, size[[2]] + Dimensions[template][[2]] - 2],
    1]]

ElementsCombine[Verbatim[_], x_] := x
ElementsCombine[x_, Verbatim[_]] := x
ElementsCombine[x_, y_] := If[SameQ[x, y], x, Throw[Nothing]]

RowsCombine[row1_, row2_] := 
 Catch[MapThread[ElementsCombine, {row1, row2}]]

ReadByDiagonals[size_] := 
 With[{ord = Catenate@Table[{i, j}, {i, size[[1]] }, {j, size[[2]] }]},
  Position[ord, #][[1, 1]] & /@ SortBy[ord, {Total[#], #} &]]

GenerateCover[method : (DepthFirstSearch | BacktrackSearch),
  levelData_, stateUpdate_, size_List, 1] := 
 If[SameQ[#, {}], $Failed,
    Partition[Last[#], size[[2]]]
    ] &@method[Table[_, Times @@ size],
   levelData, stateUpdate, True &, 1]

GenerateCover[method : (DepthFirstSearch | BacktrackSearch),
  levelData_, stateUpdate_, size_List, count_] := 
 If[SameQ[#, Nothing], $Failed,
    Partition[Last[#], size[[2]]]] & /@ method[Table[_, Times @@ size],
   levelData, stateUpdate, True &, count]

GenerateCover["BreadthFirst", levelData_, stateUpdate_, size_List,
  count_ : All (*useless here*)] := 
 Map[Partition[#, size[[2]]] &, Fold[
   Union@Catenate[Outer[stateUpdate, #1, #2, 1]] &,
   {Table[_, Times @@ size]}, levelData]]

GenerateCover[levelData_, stateUpdate_, size_List,
  opts : OptionsPattern[{Method -> "BreadthFirst", Count -> 1}]
  ] := GenerateCover[OptionValue[Method],
  levelData, stateUpdate, size, OptionValue[Count]]

GenerateCover[levelData_, stateUpdate_, size_Integer,
  opts : OptionsPattern[{Method -> "BreadthFirst", Count -> 1}]
  ] := GenerateCover[levelData, stateUpdate, {size, size}, opts]

TemplatesToLevelData[templates_, size_Integer
  ] := TemplatesToLevelData[templates, {size, size}]

TemplatesToLevelData[templates_, size_List] := Transpose[
   (Catenate /@ AllTemplates[#, size]) & /@ templates 
   ][[ReadByDiagonals[
    size + Dimensions[templates][[2 ;; 3]] - {1, 1}]]]

GenerateTemplatePattern[templates_, size_,
  opts : OptionsPattern[{Method -> "BreadthFirst", Count -> 1}]
  ] := GenerateCover[TemplatesToLevelData[templates, size],
  RowsCombine, size, opts]

Now let's see what it can do. For a shallow search on an easy tile set, depth first goes about as fast as breadth first:

tempTest = Union@Flatten[Partition[Table[Mod[i + j, 4],
      {i, 0, 6}, {j, 0, 6}], {2, 2}, {1, 1}], 1];

AbsoluteTiming[
   Length@GenerateTemplatePattern[tempTest,
     20, Method -> #, Count -> All]
   ] & /@ {"BreadthFirst", DepthFirstSearch, BacktrackSearch}

Out[] = 1.4, 1.4, 1.4

If we just want to generate one template-consistent pattern, we can pass Count option to one of the backtrackers: 

ArrayPlot[GenerateTemplatePattern[tempTest,
  20, Method -> DepthFirstSearch, Count -> 1],
 ColorRules -> {1 -> Red, 2 -> Green, 3 -> Blue, 0 -> Yellow}]

mod pattern

And the relevant times are:

AbsoluteTiming[
   Length@GenerateTemplatePattern[tempTest,
     20, Method -> #, Count -> 1]
   ] & /@ {"BreadthFirst", DepthFirstSearch, BacktrackSearch}

Out[] = 1.3, 0.35, 0.35

The times for DepthFirstSearch and BacktrackSearch indicate the algorithms are doing the same things in the same times, even though they are written slightly different. Both methods are much faster than what we currently have at WFR, which takes an unreasonable 400 seconds to do a similar calculation. That's a much bigger slowness factor than we get comparing to GenerateTiling :

GenerateTiling = ResourceFunction["GenerateTiling"];
AbsoluteTiming[GenerateTiling[tempTest, {}, 20];][[1]]
Out[] = 0.1

Now we can generate some data by varying the pattern size, and plot: 

dataGT1 =  AbsoluteTiming[Length@GenerateTiling[tempTest, {}, #]] & /@ Range[20];

dataGC1 = AbsoluteTiming[Length@GenerateTemplatePattern[tempTest,
       #, Method -> BacktrackSearch, Count -> 1]] & /@ Range[20];

Row[Show[#, ImageSize -> 250] & /@ {
   ListPlot[{Reverse /@ dataGT1, Reverse /@ dataGC1}, 
    PlotRange -> All],
   Show[Plot[1, {x, 0, 20}],
    ListPlot[dataGT1[[All, 1]]/dataGC1[[All, 1]]],
    PlotRange -> All]}, Spacer[20]]

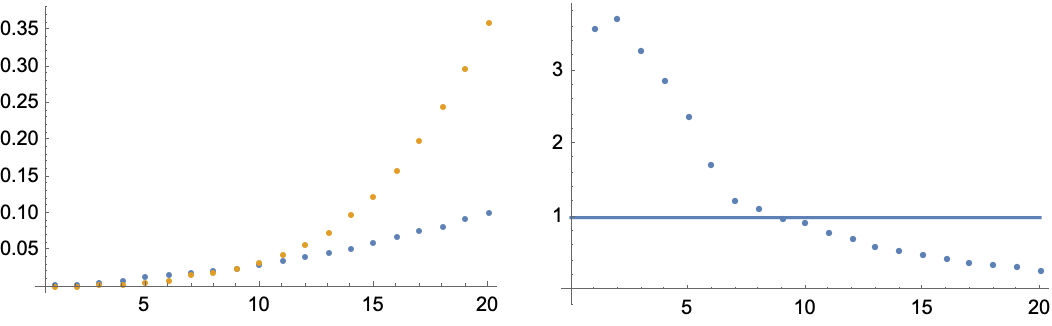
timing comparison

This data actually recapitulates what other researchers have found, that SAT solving methods can lose on the low end to backtracking algorithms, while still going faster in the long run. Here the crossover occurs for a grid size about $10 \times 10$.

Perhaps we could potentially save time in comprehensive subset searching doing small-grid eliminations using the cover method? Yes, it's a possibility, but only if breadth first is fast enough. As inputs become more complex, search trees get deeper and backtracking algorithms can easily get lost in state space and end up wasting time. Perhaps beam searching could be useful, but often the answer for getting better times is not to make things more complicated.

Instead of worrying more about times, let's talk about scope. Backtracking algorithms are a decent way to solve a wide range of combinatorial problems (some of which could even be quite practical). Some of the typical examples are solving sudoku or the eight queens puzzle:

With[{data = DeleteDuplicatesBy[
     GenerateCover[Map[Flatten,
       QueenCoversData[{8, 8}], {2}],
      RowsCombine, {8, 8}, Method -> "BreadthFirst"],
     Sort[ResourceFunction["ArrayRotations"][#]] &] /. {1 -> 2}},
 Grid[Partition[
   ResourceFunction["CharacterArrayPlot"][
      Plus[#, Table[Mod[i + j, 2], {i, 8}, {j, 8}]],
      ColorRules -> {x_ :> 
         Association[0 -> Lighter[Yellow, .6], 
           1 -> Lighter[Orange, .6]][Mod[x, 2]]},
      "CharacterRules" -> {1 -> "", 0 -> "", 
        x_ :> FromCharacterCode[9819]},
      "CharacterStyleRules" -> {x_ :> {16, Black}},
      MeshStyle -> Directive[Gray, Thick],
      ImageSize -> 200
      ] & /@ data, 3], Spacings -> {1, 1}]]

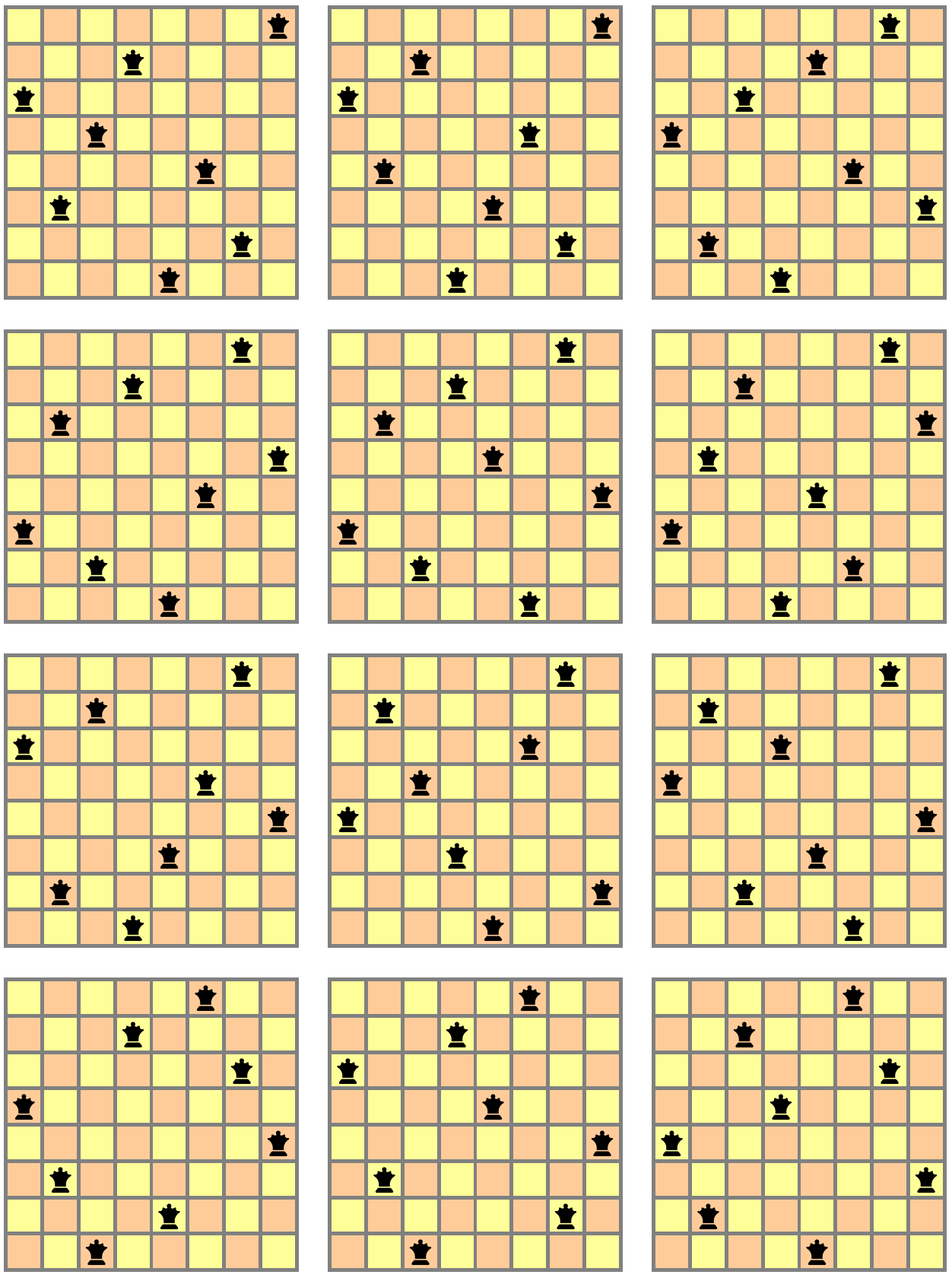
queens solutions

It's really an easy problem. To calculate the entire set of 92 it took me only 0.4 seconds, and to calculate just one solution, only .05 seconds. But I left out the code, how did I do this? Can any of the summer school students do much better?
POSTED BY: Brad Klee

enter image description here -- you have earned Featured Contributor Badge enter image description here Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!
POSTED BY: EDITORIAL BOARD

Group Abstract Group Abstract