Which one of the people on photos below you recognize? There is quite a bit of research on facial symmetry linking it to some psychological, genetic, biological, and other phenomena. There are some curious facts, for example. While speaking ~ 76% of people tend to express greater amplitude of movement on the right side of their mouth. There is a potential link to the 'big-five' personality traits: openness, conscientiousness, extraversion, agreeableness, and neuroticism. As we age accumulated progressive changes in the soft tissues of the face tend to increase asymmetry with time.
There is an interesting test to visualize asymmetry: compose (via cut & reflection) left with left side and right with right side portraits and compare them. As you can see on the photos below.


But there is a question can we automate this process? To us it is easy to understand where the axis of symmetry passes, but can a computer understand this? Especially for more asymmetric faces? In Wolfram Language there are perhaps many approaches to the problem. Here is one with ImageDistance as a measure for an optimization problem. Given pretty symmetric portrait of Lincoln:

Lets define a function that can compare left and right "unequal halves" of an image i that is split vertically at pixel column x.
splitF[i_, x_] := ImageDistance[
ImageTake[i, All, {1, x}],
ImageReflect[ImageTake[i, All, {x, -1}],Left -> Right],
DistanceFunction -> "MeanReciprocalSquaredEuclideanDistance"]
Now lets run x for several values around the middle and see where the minimum is:
i = Import["http://wolfr.am/1phd1R2"];
ImageDimensions[i]
Out[] = {400, 555}
ListPlot[splitL = Table[{splitF[i, k], k}, {k, 175, 225}]]
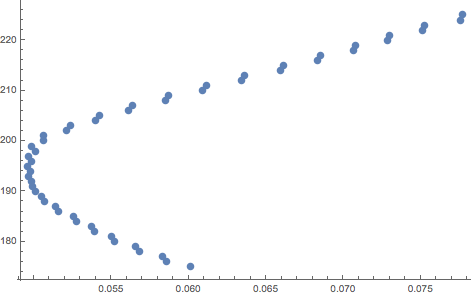
Sort[splitL];
split = %[[1, 2]]
Out[]= 195
Now lets cut at column 197 and assemble the left- and right-symmetric faces - you will get the double Lincoln portrait sown above.
ImageAssemble@{ImageAssemble[{ImageTake[i, All, {1, split}],
ImageReflect[ImageTake[i, All, {1, split}], Left -> Right]}],
ImageAssemble[{ImageReflect[ImageTake[i, All, {split + 1, -1}],
Left -> Right], ImageTake[i, All, {split + 1, -1}]}]}
Lets do the same thing with John Lennon but using a different DistanceFunction:

g = Import["http://wolfr.am/1phd6UP"];
splitF[i_, x_] := ImageDistance[
ImageTake[i, All, {1, x}],
ImageReflect[ImageTake[i, All, {x, -1}],Left -> Right],
DistanceFunction -> "MeanPatternIntensity"];
ListPlot[splitL = Table[{splitF[g, k], k}, {k, 175, 225}]]
split = Sort[splitL][[1, 2]];
ImageAssemble@{ImageAssemble[{ImageTake[g, {1, -1}, {1, split}],
ImageReflect[ImageTake[g, {1, -1}, {1, split}], Left -> Right]}],
ImageAssemble[{ImageReflect[ImageTake[g, {1, -1}, {split + 1, -1}],
Left -> Right], ImageTake[g, {1, -1}, {split + 1, -1}]}]}
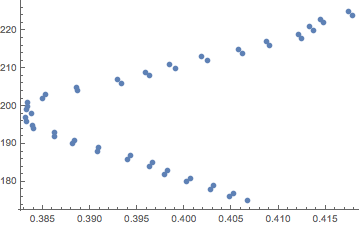
Again you will get the double portrait of Lennon show at the top. Note the graph is different. Also the split column of curse is different. Choosing different DistanceFunction may give a very different result.