
How come something that does not move is nevertheless perceived as moving? This post on Twitter by Jacob Yates explains illusions in motion perception and inspired me to look into it using Mathematica. The theory behind this illusion of motion, is explained by Adelson and Bergen in their article:
Spatiotemporal energy models for the perception of motion
A video is a sequence of frames (still images) changing over time and can be represented as an x - y - t space. The frames are then cross sections perpendicular to the t-axis. To detect movement in the video, we make cross sections perpendicular to the x- or y-axis. Here is simple video containing a static and a moving vertical line:
AnimatedImage[
Table[Image[
Graphics[{AbsoluteThickness[25], Red,
Translate[Line[{{0, -1}, {0, 1}}], {x, 0}], Blue,
Line[{{0, -1}, {0, 1}}]}, PlotRange -> 1.25],
ImageSize -> {200, 200}], {x, -1, 1, .1}]]
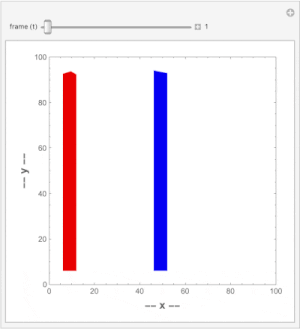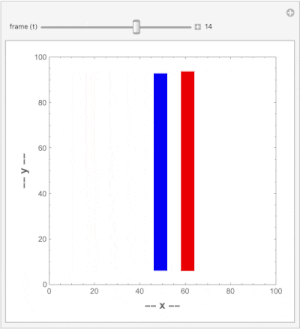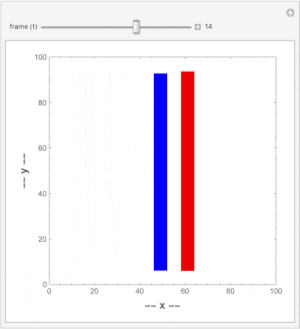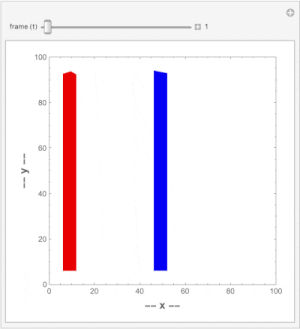
If we make a cross section perpendicular to the y-axis, we see the static (blue) line mapped as a vertical line and the moving (red) line is mapped as a slanted one.
ImageGraphics[
ImageAssemble[
Table[{ImageTake[vfLstL[[frm]], {30}]}, {frm, 1, 21, 1}]],
AspectRatio -> 1, Frame -> True,
FrameLabel -> (Style[#, Bold, 14] & /@ {"-- x --", "frame (t)"}),
ImageSize -> 350]
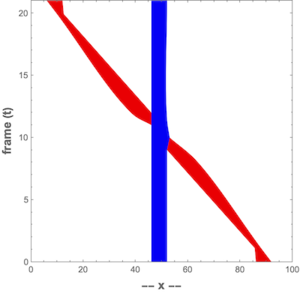
According to the above article, motion is perceived when there is orientation in x - y - t space . In our case , motion will only be observed when there is slant in the x - t diagram . We converted a video to an x-t diagram but we can equally convert an x-t diagram to its corresponding video. Here is a function that does this:
makeVideo[xtDgm_] :=
Module[{w, h}, {w, h} = ImageDimensions[xtDgm];
FrameListVideo[
Map[Image[ParallelTable[PixelValue[xtDgm, {x, #}], h, {x, w}]] &,
Range[h]], FrameRate -> 30]]
Movement in a video means slant in the x-t diagram. A simple case is that of moving vertical lines. Here is the x-t diagram and the video derived from it:
xtDgm = Image[
Graphics[
Table[{AbsoluteThickness[8], Line[{{0, d}, {1, 1 + d}}]}, {d, -1,
1, .1}], PlotRange -> {{0, 1}, {0, 1}}], ImageResolution -> 20,
ImageSize -> 100]

makeVideo[xtDgm]

For our demonstration, we want only the left- and rightmost lines to move. For that we need an x-t diagram with lines that are slanted only at both ends:
xtDgm2 =
Image[Graphics[
Table[{{AbsoluteThickness[9],
Line[{{0,
d}, {.2, .2 + d}, {.8, .2 + d}, {1, .4 + d}}]}}, {d, -.5,
1, .1}], PlotRange -> {{0, 1}, {0, 1}}], ImageResolution -> 20,
ImageSize -> 100]

makeVideo[xtDgm2]

To perfect this, we need filled and partially slanted strips to fill our x-t diagram. These two functions achieve this for both right- and left moving lines:
edgedStripR[y_, w_, h_, d_,
col_] :=(*y is y position of center, w is 1/2 of total width, d is \
fraction of 1/2 w, h is 1/2 of total height, col is the filling color*) \
{col, Polygon[{{-w + d w, y - h}, {-w, y - h - d w}, {-w,
y + h - d w}, {-w + d w, y + h}, {w - d w, y + h}, {w,
y + h + d w}, {w, y - h + d w}, {w - d w, y - h}}]}
edgedStripL[y_, w_, h_, d_, col_] := {col,
Polygon[{{-w + d w, y - h}, {-w, y - h + d w}, {-w,
y + h + d w}, {-w + d w, y + h}, {w - d w, y + h}, {w,
y + h - d w}, {w, y - h - d w}, {w - d w, y - h}}]}
Graphics[edgedStripR[0, 2, .2, .2, Gray], Axes -> True,
PlotRange -> {{-2.2, 2.2}, .5 {-1.5, 1.5}}, ImageSize -> Medium]

From this, we construct right and left x-t diagrams...
{imR, imL} =
Table[ImageResize[
ImageCrop@
ImageCrop[
Image[Graphics[
MapThread[
plt[#1, 1, .15, .2, #2] &, {Range[-1.9, 2, .1],
Flatten@Table[{Black, White}, 20]}]],
ImageResolution -> 30], {125, 162}], {50,
50}], {plt, {edgedStripR, edgedStripL}}];
Row[{imR, imL}]

...and convert them to the corresponding videos:
{vR, vL} = makeVideo /@ {imR, imL};
{goingR, goingL} =
Table[VideoFrameMap[
ImagePad[#, 10, Padding -> Lighter[Gray, .25]] &,
v], {v, {vR, vL}}];
vv = VideoTimeStretch[GridVideo[{goingL, goingR}], 3]

Many variations are now possible, only limited by our imagination:
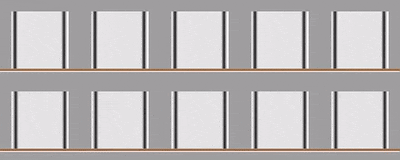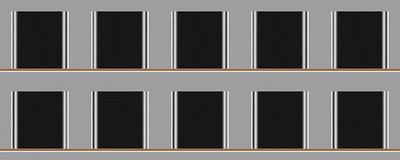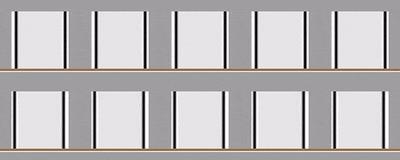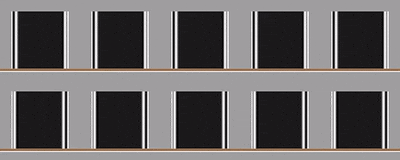
{vU, vD} = (VideoFrameMap[ImageRotate, #1] &) /@ {vR, vL};
videoRLUD =
VideoTimeStretch[
GridVideo[{{vU, vR, vR, vR, vD}, {vU, vD, vL, vL, vD}, {vU, vD,
Missing[], vU, vD}, {vU, vD, vR, vU, vD}, {vU, vL, vL, vL, vD}},
Spacings -> 5, Background -> Lighter[Gray, 0.5]], 2.5]

Some creativity can produce even more complicated examples. Adding color is one of those:
{vRc, vLc} = makeVideo /@ {imRc, imLc};
Table[VideoFrameMap[ImageResize[#, {50, 70}] &, v], {v, {vRc, vLc}}];
{goingRc, goingLc} =
Table[VideoFrameMap[ImagePad[#, 10, Padding -> LightGray] &,
v], {v, %}];
videoRc =
VideoFrameMap[ImageCompose[#, floor, Scaled[{.5, .125}]] &, goingRc];
videoLc =
VideoFrameMap[ImageCompose[#, floor, Scaled[{.5, .125}]] &, goingLc];
videoRLc =
VideoTimeStretch[GridVideo[{Table[videoRc, 5], Table[videoLc, 5]}],
1.5]

More complicated objects could be filled with "edged" strips and make illusions like the Mario one mentioned above!