These fusible numbers are all sets of rational numbers constructed through a simple binary operation: x ~ y.

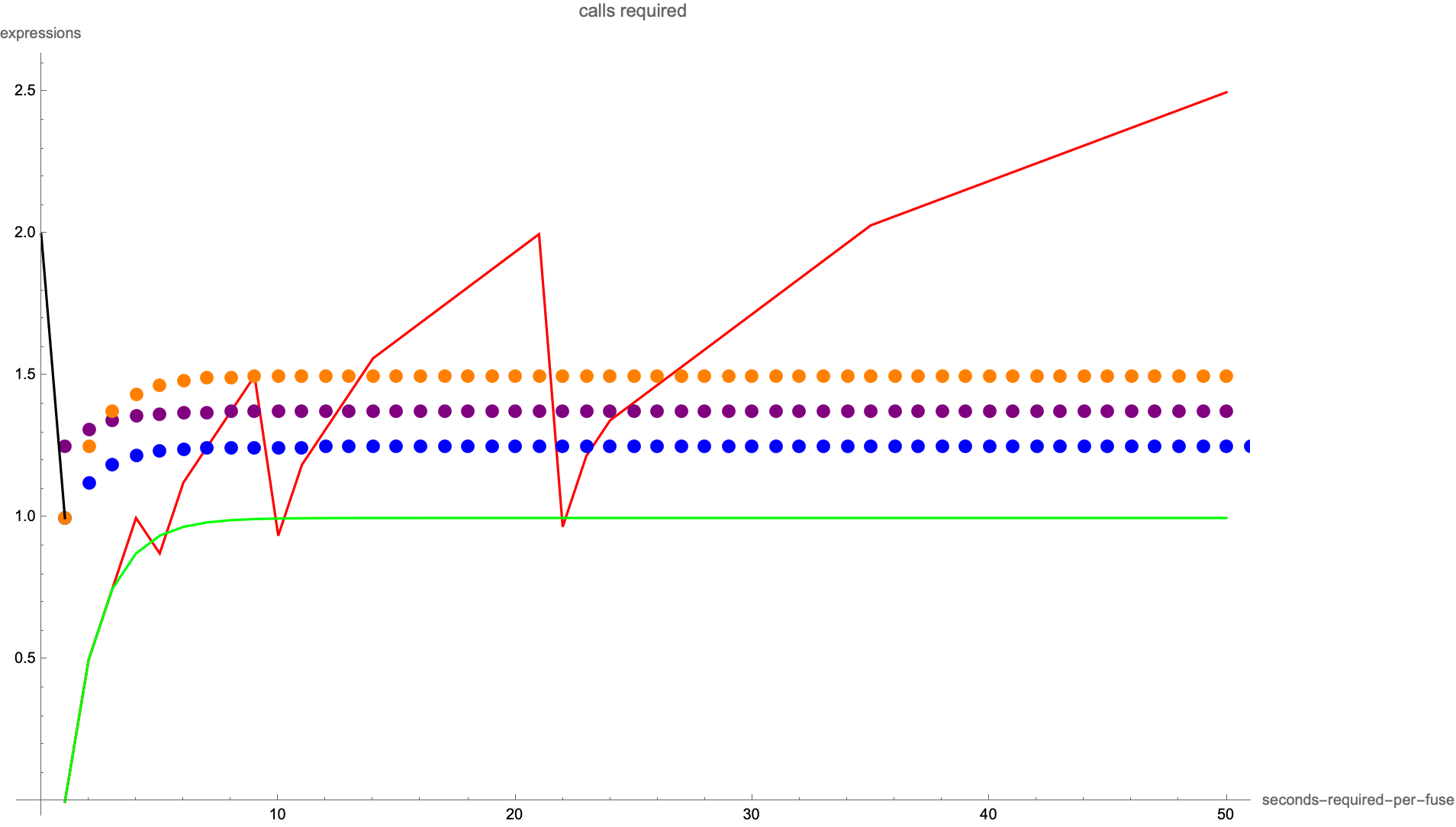
Show[ListPlot[Nest[nextFusibles, {0}, 5], PlotStyle -> {Red}, 
  AxesLabel -> {"seconds-required-per-fuse", "expressions"}, 
  PlotLabel -> "calls required", Joined -> True],
 ListPlot[fusibleN[Range[50]], PlotStyle -> {Green}, Joined -> True],
 ListPlot[fusibleN2[Range[0, 50]], PlotStyle -> {Blue}],
 ListPlot[fusibleN3[Range[50]], PlotStyle -> {Purple}],
 ListPlot[fusibleN4[Range[50]], PlotStyle -> {Orange}],
 ListPlot[partitions2[100]/50, PlotStyle -> {Black}, Joined -> True]]

That's why we can always yield rich algebraic and (transfinite) combinatorial structures. Well-ordered pure binary trees, in Schonfinkel's combinator form are made possible by this awesome, closed under addition, all I want to know is how would you burn them irregularly so that we don't know measure time by measure fuse length?

Can you measure time by measure fuse length? Why are all the fusible numbers non-negative, in R, closed under addition, and they're dyadic rationals whose denominator is a power of 2? Hypothetically, because we've already got your explanation.

fusibleGraph = TokenGraph[g, AspectRatio -> 1/2];
reversedGraph = ReverseGraph[fusibleGraph];
{DirectedGraphQ[reversedGraph], AcyclicGraphQ[reversedGraph], 
 LoopFreeGraphQ[reversedGraph]}
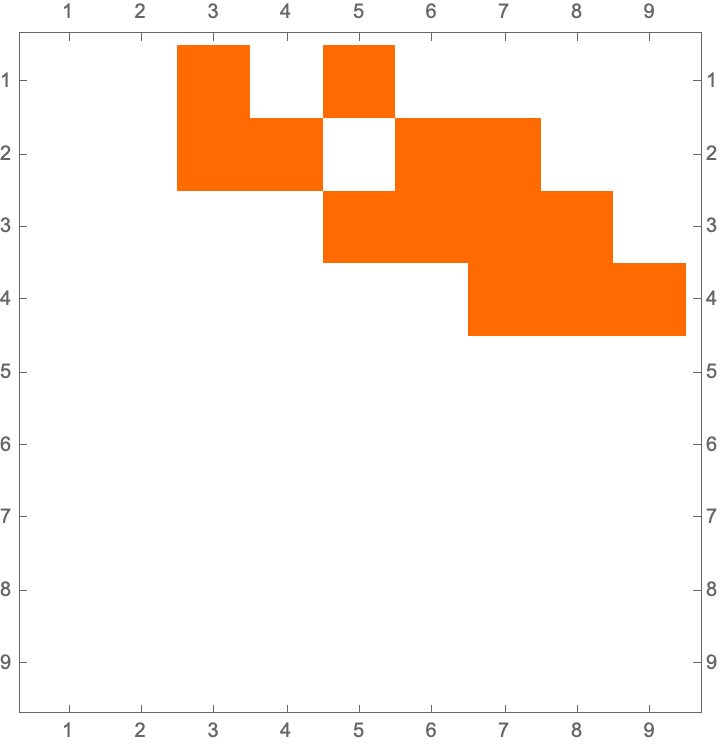
adjacencyMatrix = AdjacencyMatrix[fusibleGraph];
MatrixPlot[adjacencyMatrix]
fusibleGraph = Graph3D@fusibleGraph;
Manipulate[
 HighlightGraph[fusibleGraph, Subgraph[fusibleGraph, n]], {n, 
  VertexList[fusibleGraph]}]

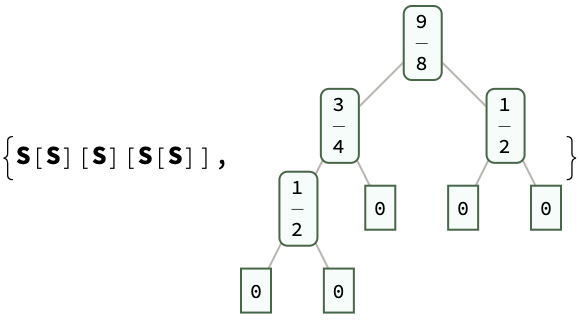
There is a deep connection between Schönfinkel's combinators and fusible numbers: both can be represented as trees. But that wouldn't change anything. The leaves of the trees are considered as 0's, and the fuse operation represents the internal nodes. If you're satisfied by that explanation, the algorithm finds only one of the partitions that work. The rational number, the number 5/4 is looking awfully problematic.

complexString5over4 = "((0~0)~0)~(0~0)";
{treeToCombinator@naughtsToTree@%,
 complexString5over4 // naughtsToTree // treeToCombinator // 
  combinatorToTree}

The algorithm requires the rational number to be changed from 3/4 to 6/8 for the decomposition to be successful, that can't be right. Which can't be right, which can't be right. That's the power of the decomposition for both fractional numbers and integers. I'm just further expanding the concept of these fusible numbers getting minimal binary tree compositions! If you hadn't told me sooner I might have deconstructed a fusible number to its minimal composition: binary tree.

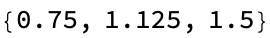
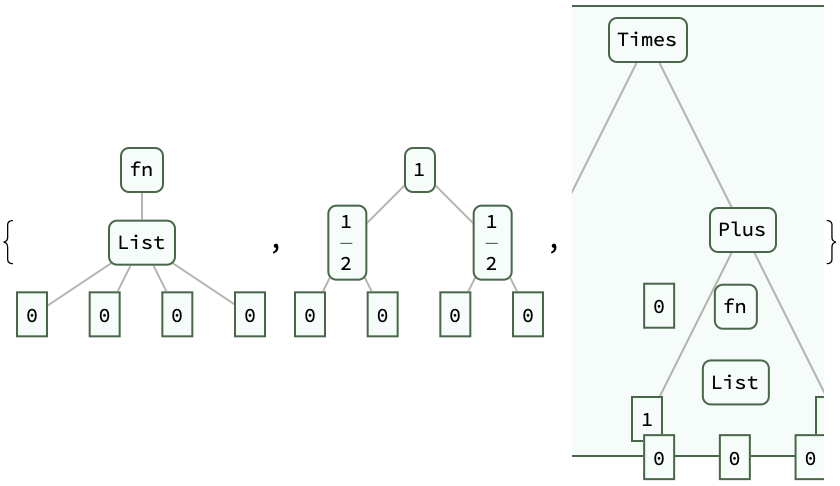
naughtsToTree /@ {"0~0~0~0", "(0~0)~(0~0)", "0~(0~0~0)"}

How can we even discuss the concept of the game of Anti-Fuse or Fuse, and their representation as binary trees? I can't wait..maybe that's just our way of calculating fusible numbers using the binary fuse operation, and embed the fusible numbers binary tree into a larger tree structure, establishing a hierarchy among the fusible numbers. Fusible numbers can be engineered differently.

t1 = "(0~(0~0))~(0~(0~0))";
t2 = "(0~0)~((0~0)~(0~0))";
treeToCombinator[naughtsToTree[t1]]
treeToCombinator[naughtsToTree[t2]]

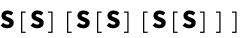
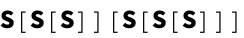
When you provide these examples of the concept of fusible numbers, maybe deconstruct them quickly so that we can explain the sum of the textual experience? It was the internal nodes that are represented and we're responsible for providing rough approximations to these irrational numbers like pi and the square root of 2 because I don't understand them, only. Only, the inefficiency of this recursive algorithm is prone to failure although it really does allow us to explore fusible numbers greater than x from all sides. A living, breathing, computationally computational infinite fusible number collection is the obstacle in creating such an algorithm. The challenge turns out to be a formula, and we made it this way due to the fast-growing nature of the fuse operation.

fuseCombine[1/2, 3/4]

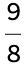
ListPlot[{fusibleN[Range[0, 15]], fusibleN2[Range[0, 15]]}, 
 PlotRange -> All, AxesLabel -> {"b", "fusibleN[b], fusibleN2[b]"}, 
 Joined -> True, PlotLegends -> {"fusibleN", "fusibleN2"}]

The challenges associated with creating a more or less generalized formula for such transitions. And I know the transition between ordinals ohm and ohm2 and the fusible numbers is transitional between the translation from fusible numbers to their corresponding ordinals and the translation from the corresponding ordinals to the fusible numbers which is amazing, to me. The concept of fusible naughts, the limit points associated with multiples of ohm, with the first accumulation point at 5/4 and the limit points converging to 3/2..what just happened?

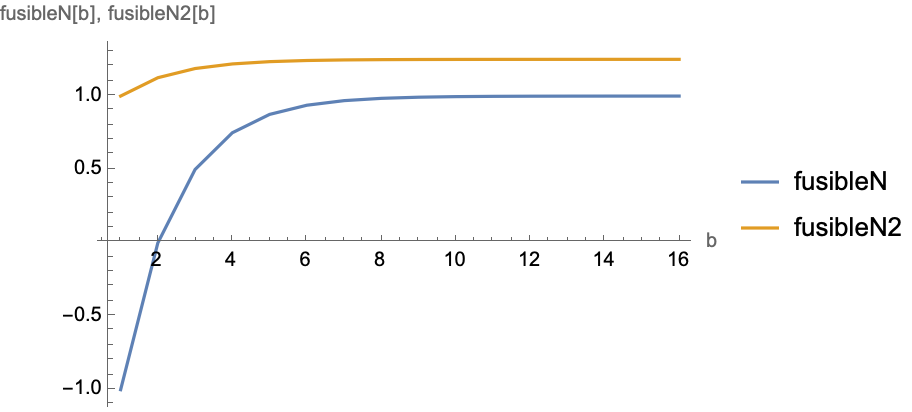
ClearAll[fusibleSequence]
fusibleSequence[n_] := 
 Table[{i, fusibleN[i], ordinalLabels[[i]]}, {i, 1, n}]
fusibleSequence[5] // TableForm

Expand upon the concept of fusible numbers, by illustrating the combinatorial distribution of fusible numbers between specific ratios, I suppose as your limit points approach past the first accumulation point at 5/4 and after the limit points converge to 3/2, maybe the collection of fusible numbers is infinite or their meaning changes. Yes, the meaning of what you have posted seems to change because what we are doing is encompassing the full complete potential of fusible numbers in approximations. Alright, now I think I finally found the default transfinite number usage in problem-solving. I don't believe the best of this newfangled transfinite/ordinal arithmetic in Mathematica. I don't know what I would do without you. 0 is the starting point for fusion, located at the bottom which is quite refreshing, really. What are the key terms referencing?

Manipulate[Nest[nextFusibles, {0}, n], {n, 0, 10, 1}]

fuseRandomPair[iterations_] := Module[
  {fusibles = Nest[nextFusibles, {0}, iterations]},
  fuse[RandomChoice[fusibles], RandomChoice[fusibles]]]
fusibleDensity[a_, b_, depth_] := 
 Count[#, x_ /; a <= x <= b]/Length[#] &@Nest[nextFusibles, {0}, depth]
ordinalToFusible[n_] := fusibleN[n]
Manipulate[
 Grid[
  {{"fuseRandomPair:", 
    fuseRandomPair[iterations]}, {"fusibleDensity:", 
    fusibleDensity[a, b, depth]}, {"ordinalToFusible:", 
    ordinalToFusible[n]}}],
 {{iterations, 5, "Iterations"}, 1, 10, 1}, {{a, 0, "Lower bound"}, 0,
   1, 0.1}, {{b, 1, "Upper bound"}, a, 1, 0.1},
 {{depth, 5, "Depth"}, 1, 10, 1},
 {{n, 7, "n"}, 1, 20, 1},
 ControlPlacement -> Left]

These fusible numbers can be 'engineered' differently and every special fusible number has a maximum-height representation. I always wondered how order is established among the fusible numbers. The infinite variety of fuses of different lengths that can be lit at both ends, during this narrow window of operations we can light the fuse at one end, light the lit fuse at the unlit end, and then fuse the ends of two lit fuses together. Zero is a fusible number. If b and a are fusible numbers with |b - a| <= 1, then (a+b+1)/2 is also a fusible number. But who are we to form a subset of the rational numbers, that means that there's no infinite sequence of fusible numbers decreasing..in other words, you can't keep going down forever; eventually, you will reach a minimum least value. Isn't that mystical? On here we have the iterations, the bounds, and the depth with n.

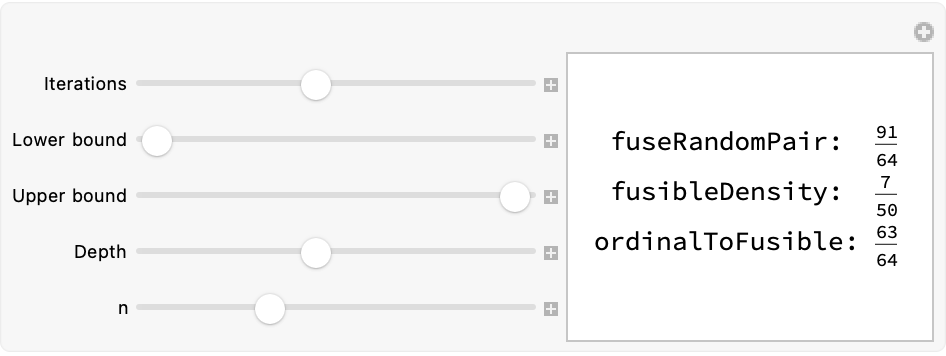
Manipulate[
 If[b >= 0, fusibleN[b], "b >= 0"], {b, 
  Range[-1, 50, 1], ControlType -> Slider}]

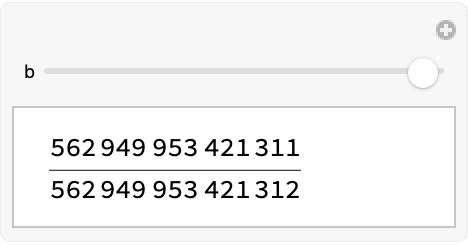
Maybe you could resize the window to get a visual of these..approximate studies of fusible numbers. Fusible numbers are relatively new. @Ranel Pärna With regard to their properties researchers are still discovering more, for example, the value slightly greater than 2 is the smallest non-fusible number.

histogramFusibles[depth_] := 
 Histogram[Nest[nextFusibles, {0}, depth], Automatic, "Probability", 
  ChartStyle -> "SolarColors", 
  ChartBaseStyle -> EdgeForm[{Dashed, Darker@LightBlue}], 
  Axes -> True, PlotRange -> All, 
  AxesLabel -> {"Fusible Numbers", "Probability"}, 
  PlotLabel -> "Histogram of Fusible Numbers"]
histogramFusibles[5]

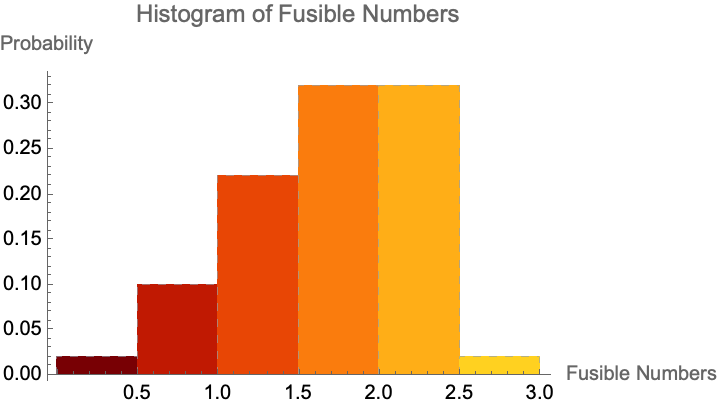
I am always so happy to see that we can find something like the smallest non-fusible number that is (3 - Sqrt(5))/2..you can't get this number by fusing other fusible numbers together, according to the rules. This result is surprising news, and in no particular order an arbitrary rational number can exist and the problem of deciding fusibility is "Undecidable", which is, and it is, shared with some of the most notorious problems in mathematics. In these difficult computer science issues like the Halting Problem, you never know when you might need to represent these fusible numbers as binary trees with the zeroes as leaves and 'fuse operation' also known as ~, acting as the internal nodes.

FusibleToOrdinal[b_] := \[Omega]^(b - 1)
OrdinalToFusible[ordinal_Integer] := ordinal - 1
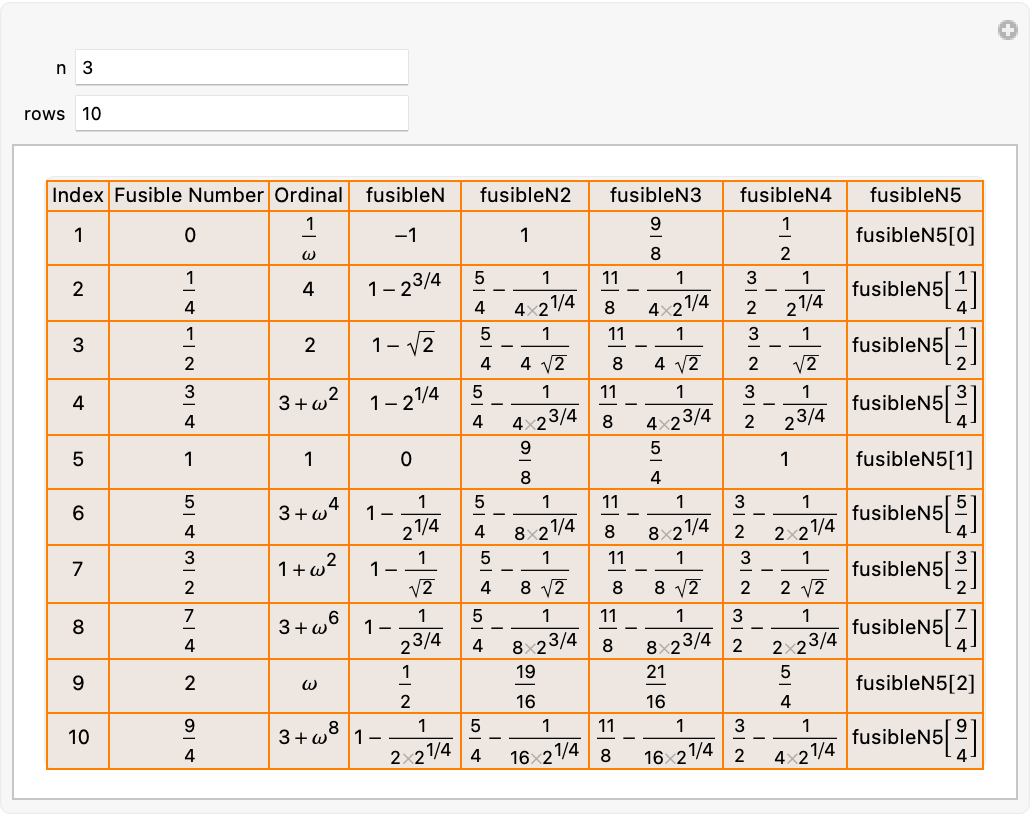
Manipulate[Panel[Grid[Join[{
     {"Index", "Fusible Number", "Ordinal", "fusibleN", "fusibleN2", 
      "fusibleN3", "fusibleN4", "fusibleN5"}},
    MapIndexed[
     Function[{row, index}, Prepend[row, First@index]],
     Take[Table[{
        fusible,
        FusibleToOrdinal[fusible],
        fusibleN[fusible],
        fusibleN2[fusible],
        fusibleN3[fusible],
        fusibleN4[fusible],
        fusibleN5[fusible]},
       {fusible, Range[0, n, 1/4]}
       ], rows]]], Frame -> All,
   Background -> RGBColor[0.6, 0.3, 0.1, 0.1],
   FrameStyle -> Directive[Thin, Orange]],
  FrameMargins -> 0],
 {{n, 3}, 0, 10, 1,
  "Number of Fusible Numbers"},
 {{rows, 10}, 1, 20, 1,
  "Number of Rows"}]

{N[First[fuseApprox[Sqrt[2], 5]]], N[First[fuseApprox[Pi, 5]]]}

These grids, we finally got the default grids! The nice geometric representation to these numbers links them to the other, areas of computer science and mathematics. The closest thing we have to a Hilbert space is the sign of an inactive, set of fusible numbers that is well-ordered. Now what this means, is that for any nonempty subset of fusible numbers there's a least element and furthermore it's a deep concept in set theory, well-ordering is. This is one of set theory's best kept secrets. And this only works if the fusible numbers include all certain rational numbers, whatever those are. And non-negative integers. And the gaps in the set. For instance, there are ranges of numbers that contain no fusible numbers at all. This confirms that, the size of these gaps, and the distribution of fusible numbers, are areas of research that are ongoing. This is happening now.

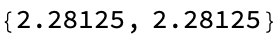
FusibleToOrdinal[b_] := \[Omega]^(b - 1)
OrdinalToFusible[ordinal_Integer] := ordinal - 1
With[
 {mValues = Reap[m[2]], maxXRange = 60},
 Manipulate[
  Show[
   ListLinePlot[
    Take[mValues[[2, 1]], UpTo[xRange]],
    ImageSize -> 800,
    AspectRatio -> 1/10,
    PlotTheme -> "Detailed",
    GridLines -> {None, {mValues[[1]]}},
    PlotRange -> {{0, maxXRange}, {0, 1}},
    Method -> {"GridLinesInFront" -> True},
    ColorFunction -> (Blend[{Blue, White}, #] &),
    GridLinesStyle -> Directive[Thickness[0.001], Red]
    ],
   ListPlot[
    Take[mValues[[2, 1]], UpTo[xRange]],
    PlotStyle -> Directive[PointSize[1/107], Green]
    ]
   ],
  {xRange, 1, maxXRange, 1},
  Frame -> True,
  ControlPlacement -> Bottom
  ]
 ]

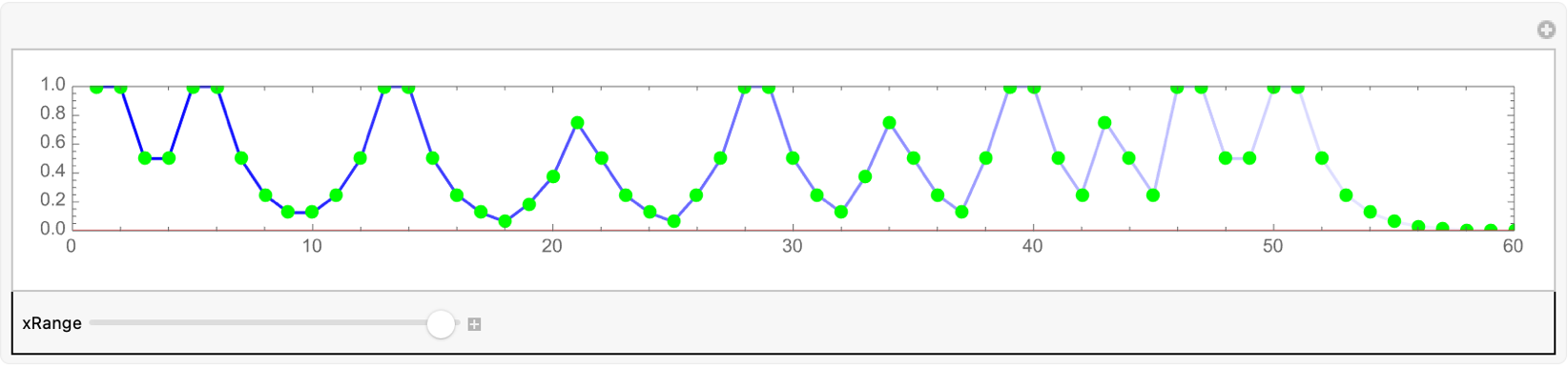
For every natural number n, there exists a smallest fusible number larger than n. And with that true, there exists an algorithm, M, which cannot be proven to terminate, within the constraints of Peano Arithmetic, for all natural inputs. Even though it does in fact terminate, for real inputs. That's a reflection and it really does come down to that, of visualizations of representations of binary trees...

DynamicModule[{num = 1/2}, 
 Column[{"Choose a fusible number, to decompose:", 
   Slider[Dynamic[num], {0, 3, 1/8}], 
   Dynamic[decompose[num] // TreeForm]}]]

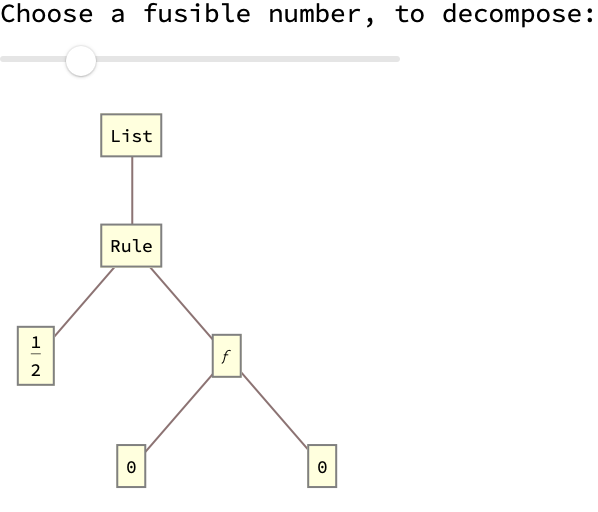
Manipulate[
 Groupings[ConstantArray[Tree[0, None], n], 
  FuseTree -> {2, Orderless}], {{n, 5, "Number of Nodes"}, 1, 15, 1}, 
 FrameMargins -> 0, Paneled -> False]

There are some several realistic statements that can be expressed within the system of Peano Arithmetic, but which cannot be proven within it, but which can provide further examples and get some action out of Gödel's incompleteness theorem. They are an algorithm to determine in this universe whether a given real number is fusible or not, in the hall of all its limit points the set of fusible numbers is closed, in though the context of fusible numbers the behavior of the "so-called exponent" of dyadic fractions.

fusibleNumbersPerIterations = 
  Table[Nest[nextFusibles, {0}, n], {n, 1, 5}];
fuseApproxN[x_, n_] := 
 If[x < 0, -fuseApprox[-x, n], fuseApprox[x, n]]
fusibleTimings = Table[
   {i, First@
     Block[{$RecursionLimit = 10^4}, RepeatedTiming[fusibleN[i]]]},
   {i, Join[Range[2, 5], Range[10^2, 10^3, 10^2]]}];
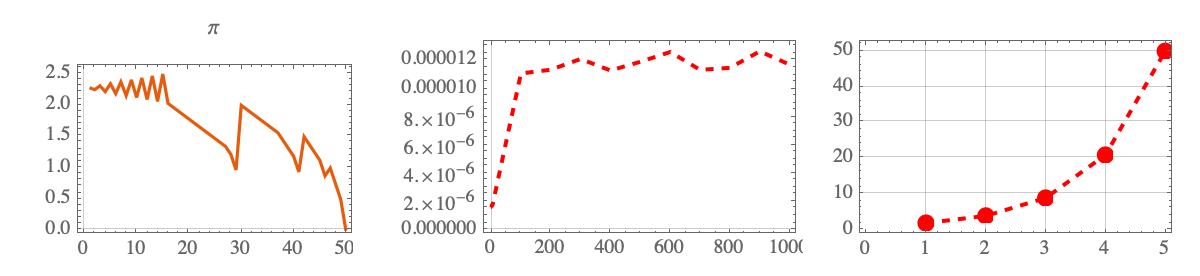
GraphicsRow[{
  ListLinePlot[
   fuseApproxN[Pi, 5],
   PlotLabel -> Pi,
   PlotTheme -> "Scientific"],
  ListLinePlot[
   fusibleTimings,
   PlotTheme -> "Scientific",
   PlotStyle -> {Red, Thick, Dashed}],
  ListPlot[
   Length /@ fusibleNumbersPerIterations,
   Joined -> True,
   GridLines -> Automatic,
   PlotTheme -> "Scientific",
   PlotMarkers -> {Automatic, 10},
   PlotStyle -> {Red, Thick, Dashed}]
  }]

Also, do you know please that we can embrace the change that our modern society presents, a symbol of the inevitable that is soon to come? Explaining these fusible numbers could be as simple as holding up a smartphone with a QR code. No coins, no crumpled bills, just a technological bridge where you will find that we can reach one another, make a difference. @Ranel Pärna This project begs for some refreshments, the mathematical riddle about measuring time using fuses. All since they can be fused together from 0 using the binary fuse operation, and yes they are well-ordered. The binary fuse operation, this operation involves calculating the average of x and y, two fusible numbers they are and adding 1/2 with the difference between x and y, less than 1.

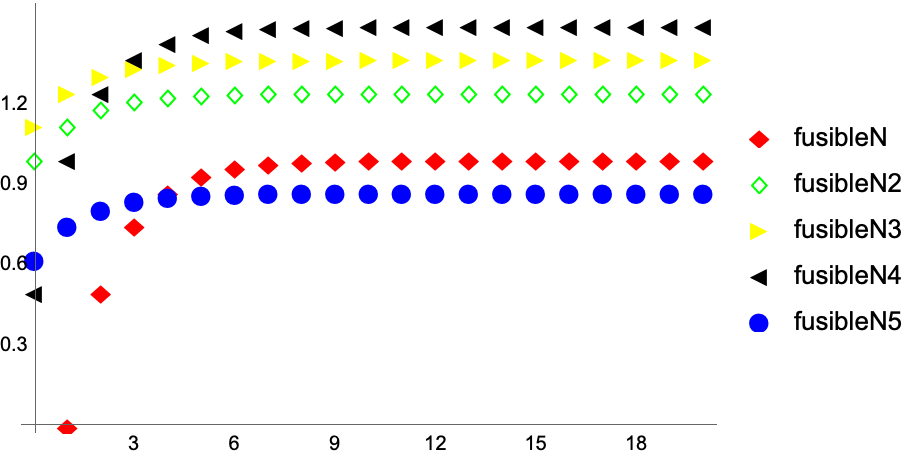
ClearAll[fusibleN1, fusibleN2, fusibleN3, fusibleN4];
fusibleN1[b_] := 1 - 2^(-1 - (b - 2));
fusibleN2[b_] := 5/4 - 2^(-1 - (b + 1));
fusibleN3[b_] := 11/8 - 2^(-1 - (b + 1));
fusibleN4[b_] := 3/2 - 2^-(b + 1) - 2^-(b + 1);
fusibleN5[b_] := 7/8 - 2^(-1 - (b + 1));
fusibleFns = {
   fusibleN,
   fusibleN2,
   fusibleN3,
   fusibleN4,
   fusibleN5
   };
ListPlot[
 Table[
  Table[
   {x, fn[x]}, {x, 0, 20}
   ],
  {fn, fusibleFns}],
 PlotLegends -> fusibleFns,
 PlotStyle -> {
   Directive[Red, Thick],
   Directive[Green, Thick],
   Directive[Yellow, Thick],
   Directive[Black, Thick],
   Directive[Blue, Thick]
   },
 PlotMarkers -> {
   Style["\[FilledDiamond]", 15, Red],
   Style["\[EmptyDiamond]", 15, Green],
   Style["\[FilledRightTriangle]", 15, Yellow],
   Style["\[FilledLeftTriangle]", 15, Black],
   Style["\[FilledCircle]", 15, Blue]
   }, Ticks -> {
   Table[{i, i, 0}, {i, 0, 20, 3}],
   Table[{i, i, 0}, {i, 0, Max[Table[fn[20], {fn, fusibleFns}]], .3}
    ]}]

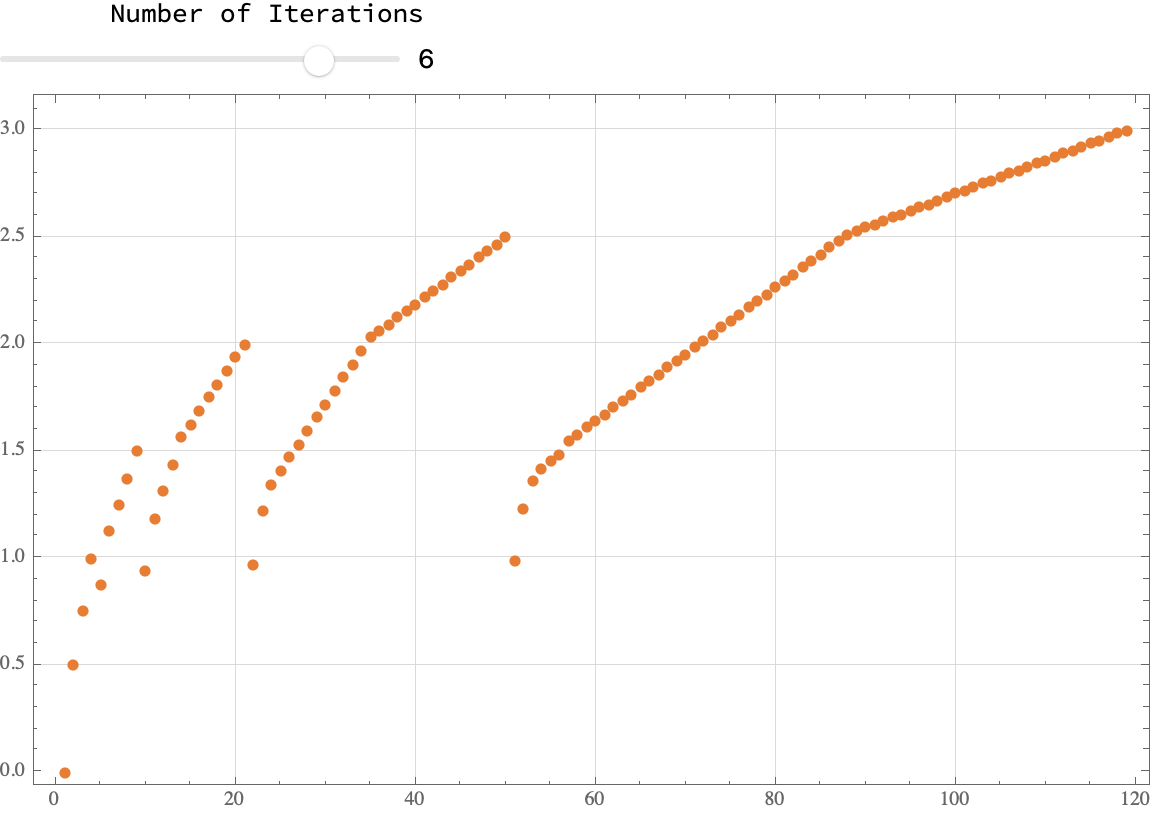
DynamicModule[{iter = 5},
 Column[
  {Labeled[
    Slider[
     Dynamic[iter],
     {1, 7, 1},
     Appearance -> "Labeled"],
    "Number of Iterations",
    Top],
   Dynamic[
    ListPlot[
     Nest[nextFusibles, {0}, iter],
     PlotRange -> All,
     ImageSize -> Large,
     Frame -> True,
     PlotStyle -> {PointSize[0.01],
       ColorData["Rainbow"][iter/7]},
     PlotTheme -> "Scientific",
     GridLines -> Automatic,
     GridLinesStyle -> LightGray]]}]]

That is the stipulation. A testament to our ability to adapt faster to the future of work, which is just something we do in our spare time. Quantum computing has been the object of serious studies...the density of these numbers grows rapidly, along the real line. The best way I can describe this is that they're not distributed evenly! Oh no..their density sharply drops and increases around accumulation points, all of a sudden, I was surprised. Okay, it takes a while and I know this is just a fascinating field of exploration in number theory relax.

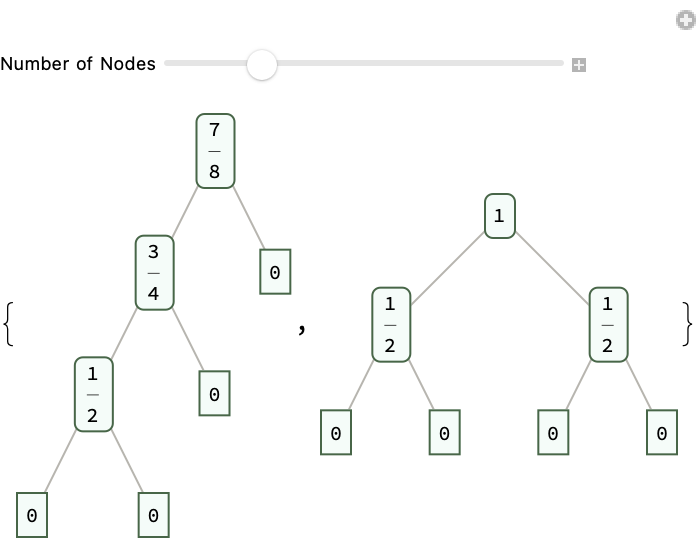
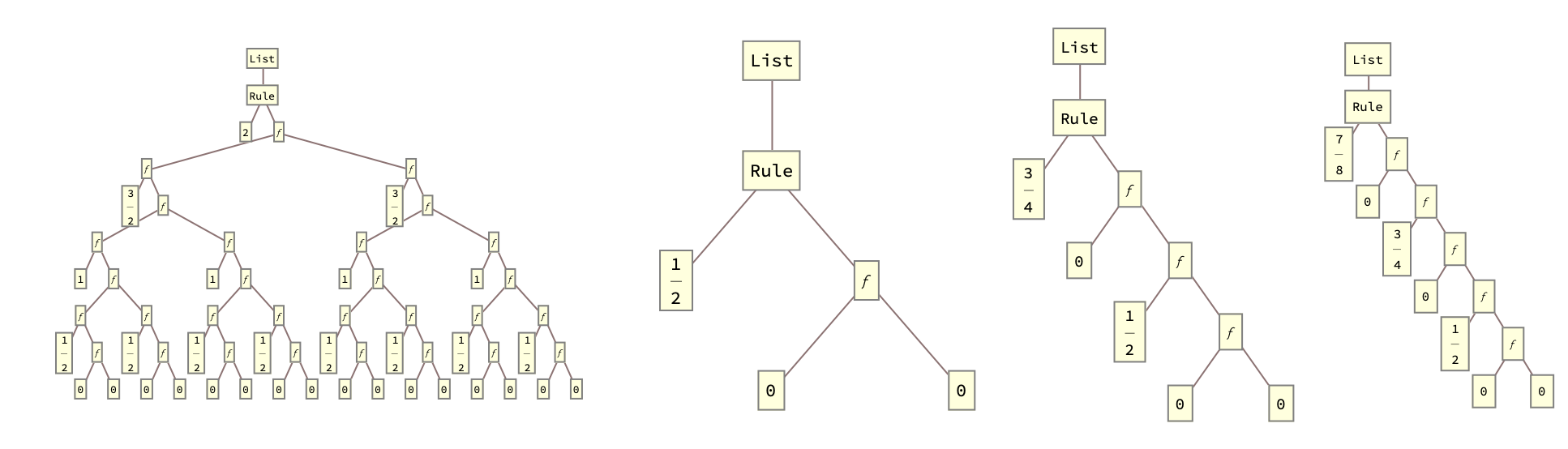
decompositionTree[n_] := TreeForm[decompose[n]]
Row[{decompositionTree[2], decompositionTree[1/2], 
  decompositionTree[3/4], decompositionTree[7/8]}]

Particularly in terms of their relation to ordinal numbers, distribution, growth, you name it Pärna do mapping of ordinal numbers to fusible numbers: limit ordinals. In Schönfinkel's combinator form their manipulation and expression has run its course. It's not about the rich combinatorial structures and rich algebra that exists outside of the implementation. It's not even about our desire to form more intriguing simple binary operations x ~ y. Because within our mental imagery within the Ruliad you will find the breadth of this mathematical riddle about measuring time using fuses which is suitable enough for our purposes.

Manipulate[
 With[
  {values = Nest[nextFusibles, initSet, 3]},
  Graphics[{ColorData["Rainbow"][RandomReal[]],
    Polygon[{{#, -0.02}, {# + 0.02, 0}, {#, 0.02}}] & /@ values},
   Axes -> {True, False},
   PlotRange -> {{0, 4}, All},
   ImageSize -> 10 72,
   AspectRatio -> 1/10]],
 Control[
  {{initSet, {1, 0.5}, "initSet"},
   ControlType -> InputField,
   FieldSize -> 15,
   Interpreter -> (ToExpression@StringSplit[#, ","] &)}]]
ordinals = {1, 1.125, 1.25, 1.5, 1.625, 1.75, 1.875, 2, 3};  
DynamicModule[
 {iter = 5},
 Column[{
   Slider[Dynamic[n, (n = #; iter = #) &], {1, 20, 1}],
   Dynamic[Nest[nextFusibles, {0}, iter] // Graphics[{
        Polygon[{{#, -0.02}, {# + 0.02, 0}, {#, 0.02}}] & /@ #,
        {Red, 
         Polygon[{{#, -0.02}, {# + 0.02, 0}, {#, 0.02}}] & /@ ordinals}
        },
       Axes -> {True, False},
       PlotRange -> {{0, 4}, All},
       ImageSize -> 10 72,
       AspectRatio -> 1/10] &]}]]

There are so many breakthroughs showing that determining whether a number is fusible is computationally "Undecidable". That means there's no algorithm that can solve this problem for all inputs in a finite number of steps. Have you tried an infinite number of steps? It's a beautiful thing, the concept of fusible numbers has the computational complexity and I know this seems like a hokey explanation, and it doesn't mean that we can't break the symbolic structure of the Wolfram Language, it doesn't mean that theory of computation.