Hi Shwetabh, you really swept me away when it comes to the expression simplification, with the leaves, the recursive subcounts, and their histograms. Supposedly we think we could do all these things..

poly = RandomReal[{-1, 1}] (x + 3) (x - 10)/(x - 3);
\[Theta] = RandomReal[{0, 2 \[Pi]}];
F[{x_, y_}] = {{Cos[\[Theta]], -Sin[\[Theta]]}, {Sin[\[Theta]], 
     Cos[\[Theta]]}} . {x, y + poly};
ListPlot[
 Table[NestList[F, {RandomReal[{-3, 0}], i/10}, 5000], {i, -20, 20}], 
 Axes -> False, ImageSize -> 800, AspectRatio -> Automatic, 
 PlotStyle -> PointSize[.001]]

This histogram polynomial, you could use it on the epidemiological models. One promise, so many possibilities & transformations. How would you classify these polynomials? Oh no what it actually is is the process of implementing a multiway system, to describe what the simplification of algebraic expressions is really trying to convey it's extraordinary. The Wolfram Language in Mathematica, language in lowercase, demonstrates the potential for transforming polynomials into multiple forms, which can often simplify complex expressions, which really just shows the unstoppable complex expression simplification. If that makes everything questionable then..fusible numbers can approximate constants. Can constants approximate fusible numbers? It was heartbreaking when I saw those complex expressions what we traditionally think of as a polynomial in a category, how polynomials can be expressed in a multitude of ways, due to their transformation properties. Unless you put safeguards in place it could not be more clear now that we can simplify away, and no one wants to have a polynomial defined. But that would be an exaggeration, that wouldn't solve anything. Supposedly all these polynomials they are to be processed and it is amazing how these expressions can be applied from a given function to a polynomial derivative and integral, with respect to x, returning a list of expressions over an arbitrary number of time steps to represent the graph, vertex count, leaf counts and outgoing & incoming edges per vertex.

Plus there's this tree structure that you mention these properties are so transformative. This article got me dreaming in Wolfram Language and that's why these graphs are so hard because they are easy, the more you understand it. When you group parts of the given polynomials that are different and apply the transformations of factor & expand, you may visualize the transformations of this polynomial. But it's not going to happen, that fast. This was a thriller, let me sort of re-do and re-remember where I was. A forerunner of the modern Mathematica Language, the dynamics of what happened with the cellular automata. At any time, I can be alone by myself at any time think, write code, ya know write things. That's one sense of being off the grid. Function repository directories. Let's just bet on you @Shwetabh Singh it's the 5% of you that is going to do fantastic things beyond what you could have achieved if you'd just been doing the large main-line institutional things.

expressionsFrom[poly_, fun_] := 
  fun /@ {poly, D[poly, x], Integrate[poly, x]};
replaceParts[poly_, fun_] := 
  MapAt[fun, poly, #] & /@ Position[poly, _];
findVertexInfo[nn_] := 
  Module[{lf, maxlf, minlf, maxlfpos, minlfpos, maxlff, minlff}, 
   lf = LeafCount /@ VertexList[nn];
   maxlf = Max[lf];
   minlf = Min[lf];
   maxlfpos = Position[lf, maxlf][[1, 1]];
   minlfpos = Position[lf, minlf][[1, 1]];
   maxlff = VertexList[nn][[maxlfpos]];
   minlff = VertexList[nn][[minlfpos]];
   <|"MaxLeaf" -> maxlf, "MinLeaf" -> minlf, "MaxLeafForm" -> maxlff, 
    "MinLeafForm" -> minlff|>];
graphInfo[graph_] := <|"VertexCount" -> VertexCount[graph], 
   "EdgeCount" -> EdgeCount[graph], 
   "VertexInfo" -> findVertexInfo[graph]|>;
polys = {(x^2 + 2 x + 1) (x - 2), (x^2 - 4) (x - 1)/(x - 2), (x^3 + 
     x^2 - x - 1), (x^4 - x^3 + x^2 - x + 
     1), (x^3 + 2 x^2 - 5 x + 1)/(x - 2)};
nestGraphs = 
  NestGraph[
     Join[expressionsFrom[#, Expand], 
       expressionsFrom[#, Factor]] &, #, 4, 
     VertexLabels -> Automatic] & /@ polys;
info = graphInfo /@ nestGraphs;
Dataset[info]

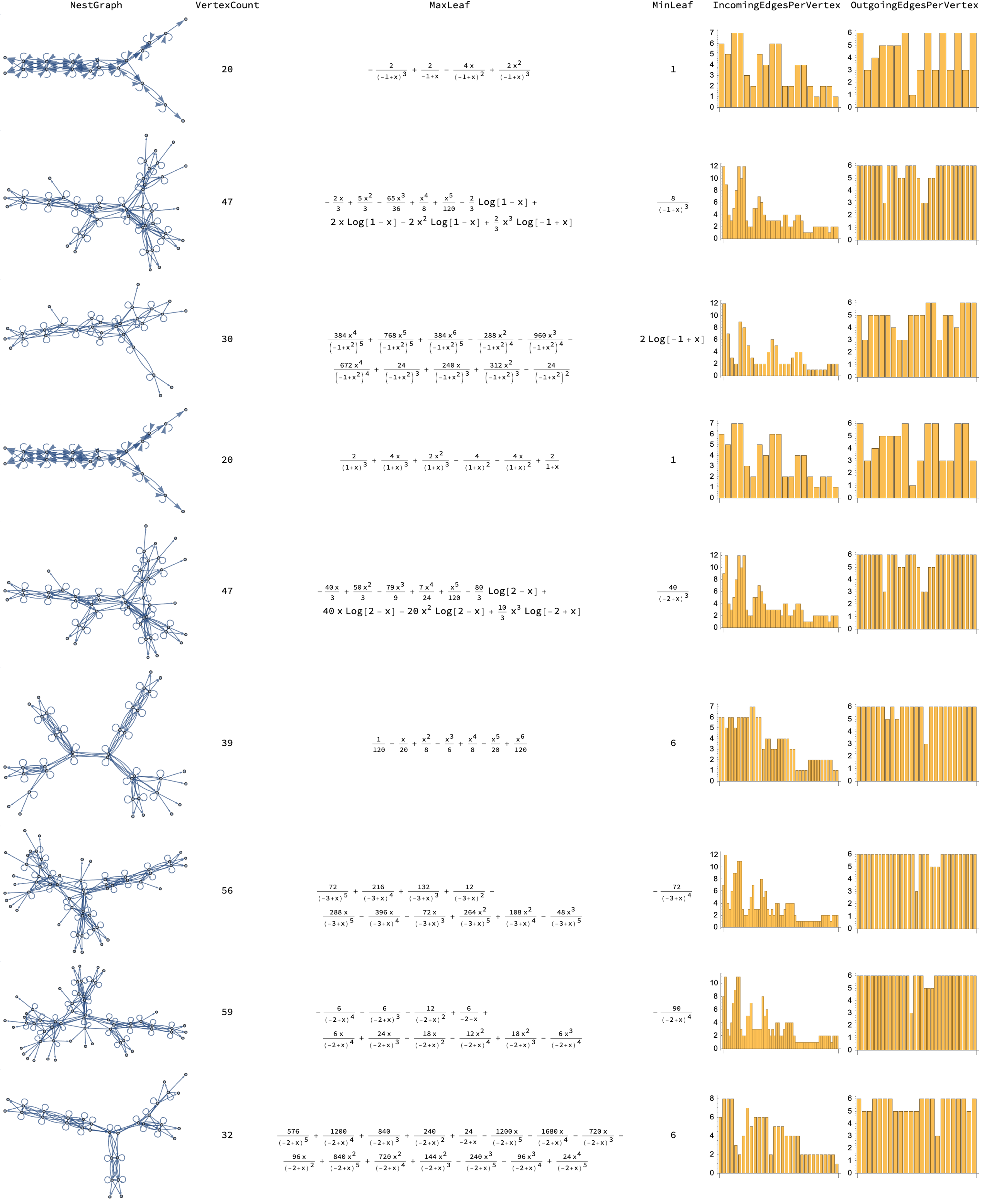
As seen on the multi-way system, where the nodes represent the transformation of the polynomial and edges represent the transformation operations..we can use and remove the NextGraph function to apply a given function recursively to the nodes in the graph. The means of defining the simplicity of an expression is the timely LeafCount function that indicates, and yes it does show that a simpler expression has fewer elements or leaves. If I discuss the limitations of the function please tell me, the transformation of the polynomial tools that introduces a recursive function as an improvement. Do you think that matters, @Shwetabh Singh ? Then you can dig deeper into the subexpression expressions thus creating more potential transformations and groupings. The maximum and minimum leaf count vertices are a delectable treat, they represent the simplest and complex forms of the polynomial. And that's a wrap!

expressionsFrom[poly_, fun_] := 
  fun /@ {poly, D[poly, x], Integrate[poly, x]};
replaceParts[poly_, fun_] := 
  MapAt[fun, poly, #] & /@ Position[poly, _];
findVertexInfo[nn_] := 
  Module[{lf, maxlf, minlf, maxlfpos, minlfpos, maxlff, minlff}, 
   lf = LeafCount /@ VertexList[nn];
   maxlf = Max[lf];
   minlf = Min[lf];
   maxlfpos = Position[lf, maxlf][[1, 1]];
   minlfpos = Position[lf, minlf][[1, 1]];
   maxlff = VertexList[nn][[maxlfpos]];
   minlff = VertexList[nn][[minlfpos]];
   <|"MaxLeaf" -> maxlf, "MinLeaf" -> minlf, "MaxLeafForm" -> maxlff, 
    "MinLeafForm" -> minlff|>];
graphInfo[graph_] := <|"VertexCount" -> VertexCount[graph], 
   "EdgeCount" -> EdgeCount[graph], 
   "VertexInfo" -> findVertexInfo[graph]|>;
polys = {(x^2 + 2 x + 1) (x - 2), (x^2 - 4) (x - 1)/(x - 2), (x^3 + 
     x^2 - x - 1), (x^4 - x^3 + x^2 - x + 
     1), (x^3 + 2 x^2 - 5 x + 1)/(x - 2)};
nestGraphs = 
  NestGraph[
     Join[expressionsFrom[#, Expand], 
       expressionsFrom[#, Factor]] &, #, 4, 
     VertexLabels -> Automatic] & /@ polys;
info = graphInfo /@ nestGraphs;
Dataset[info]

All transformed polynomials remain equivalent by evaluating them with a random number..and while we can find vertex info about the maximum and minimum leaf count that signify the thought of the measure of complexity, the number of terminals in an expression tree, the Wolfram Language used within your Association cannot be translated. You can acknowledge the function expressionsFrom, even use it with both Expand and Factor functions, even focus on how the NestGraph function applies the expressionsFrom function to generate a graph..with Expand & Factor, none of our nodes represent the transformations of the polynomial. None of the edges represent the transformation operations, that's not going to happen. These prodigious Wolfram language operations are forbidden to be described no matter how deep we dig into the expression's subexpressions, via the potential transformations and groupings, once we leave the Wolfram function repository we are able to gain a deeper understanding of polynomials, like the differentiation and integration transformations that are used in signal processing, linearly capture more complex relationships in datasets by transforming a complex polynomial into a quadratic. Which may not be true, we didn't even do anything and the polynomial just changed!