@Jan Greve that was amazing. You just got all those Riordan arrays and you could use them to model & analyze, populations that we all agree.
RiordanArray[g_, f_][n_Integer?NonNegative, k_Integer?NonNegative] :=
SeriesCoefficient[g[t]*Power[f[t], k], {t, 0, n}];
RiordanArray[g_, f_][n_Integer?NonNegative,
kStart_Integer?NonNegative ;; kEnd_Integer?NonNegative] /;
kEnd >= kStart :=
If[kStart > n, ConstantArray[0, kEnd - kStart + 1],
If[kEnd > n,
Join[(SeriesCoefficient[g[t]*Power[f[t], #], {t, 0, n}]) & /@
Range[kStart, n],
ConstantArray[0,
kEnd - n]], (SeriesCoefficient[
g[t]*Power[f[t], #], {t, 0, n}]) & /@ Range[kStart, kEnd]]];
RiordanArray[g_, f_][
nStart_Integer?NonNegative ;; nEnd_Integer?NonNegative,
k_Integer?NonNegative] /; nEnd >= nStart :=
CoefficientList[Series[g[t]*Power[f[t], k], {t, 0, nEnd}],
t][[(nStart + 1) ;; (nEnd + 1)]];
RiordanArray[g_, f_][
nStart_Integer?NonNegative ;; nEnd_Integer?NonNegative,
kStart_Integer?NonNegative ;; kEnd_Integer?NonNegative] /;
nEnd >= nStart && kEnd >= kStart :=
CoefficientList[Series[g[t]*Power[f[t], #], {t, 0, nEnd}],
t, {nEnd + 1}][[(nStart + 1) ;; (nEnd + 1)]] & /@
Range[kStart, kEnd] // Transpose;
RiordanArray /:
MatrixForm[
RiordanArray[g_,
f_], {nStart_Integer?NonNegative ;; nEnd_Integer?NonNegative,
kStart_Integer?NonNegative ;; kEnd_Integer?NonNegative}] /;
nEnd >= nStart && kEnd >= kStart :=
If[nStart == 0 && kStart == 0,
Join[Map[PadRight[#, (kEnd + 2), "\[CenterEllipsis]"] &,
RiordanArray[g, f][nStart ;; nEnd, kStart ;; kEnd], 1],
List[Join[
ConstantArray[
"\[VerticalEllipsis]", (kEnd +
1)], {"\[DescendingEllipsis]"}]]] // MatrixForm,
If[nStart != 0,
If[kStart == 0,
Join[List[
Join[ConstantArray[
"\[VerticalEllipsis]", (kEnd +
1)], {"\[AscendingEllipsis]"}]],
Join[Map[PadRight[#, (kEnd + 2), "\[CenterEllipsis]"] &,
RiordanArray[g, f][nStart ;; nEnd, kStart ;; kEnd], 1],
List[Join[
ConstantArray[
"\[VerticalEllipsis]", (kEnd +
1)], {"\[DescendingEllipsis]"}]]]] // MatrixForm,
Join[List[
Join[{"\[DescendingEllipsis]"},
ConstantArray[
"\[VerticalEllipsis]", (kEnd + 1 -
kStart)], {"\[AscendingEllipsis]"}]],
Join[Map[
PadLeft[PadRight[#, (kEnd + 2 - kStart),
"\[CenterEllipsis]"], (kEnd + 3 - kStart),
"\[CenterEllipsis]"] &,
RiordanArray[g, f][nStart ;; nEnd, kStart ;; kEnd], 1],
List[Join[{"\[AscendingEllipsis]"},
ConstantArray[
"\[VerticalEllipsis]", (kEnd + 1 -
kStart)], {"\[DescendingEllipsis]"}]]]] // MatrixForm],
Join[
Map[PadLeft[
PadRight[#, (kEnd + 2 - kStart),
"\[CenterEllipsis]"], (kEnd + 3 - kStart),
"\[CenterEllipsis]"] &,
RiordanArray[g, f][nStart ;; nEnd, kStart ;; kEnd], 1],
List[Join[{"\[AscendingEllipsis]"},
ConstantArray[
"\[VerticalEllipsis]", (kEnd + 1 -
kStart)], {"\[DescendingEllipsis]"}]]] // MatrixForm]
]
RiordanArray /:
MakeBoxes[ra : RiordanArray[g_, f_], StandardForm] :=
BoxForm`ArrangeSummaryBox[RiordanArray, ra,
ArrayPlot[RiordanArray[g, f][0 ;; 4, 0 ;; 4],
ColorFunction -> "Rainbow", ColorFunctionScaling -> True],
{{"g(t) =", g["t"]}, {"f(t) =", f["t"]}}, {}, StandardForm]
ColumnGeneratingFunction[RiordanArray[g_, f_], k_] :=
(g[#]*Power[f[#], k]) &
ColumnGeneratingFunction[RiordanArray[g_, f_],
k_Integer?NonNegative, {t_, n_Integer?NonNegative}] :=
Series[(g[t]*Power[f[t], k]), {t, 0, n}]
RiordanArray /: RiordanArray[g1_, f1_] . RiordanArray[g2_, f2_] :=
RiordanArray[g1[#]*g2[f1[#]] &, f2[f1[#]] &]
FTRA[RiordanArray[g_, f_], h_, k_] :=
ColumnGeneratingFunction[
RiordanArray[g, f] .
RiordanArray[(GeneratingFunction[h[#], k, #]) &, (1) &], 0]
RiordanArray /: Inverse[RiordanArray[g_, f_]] :=
With[{finv = InverseFunction[f]},
RiordanArray[Power[g[finv[#]], -1] &, finv[#] &]]
GetGeneratingFunctionPairs[RiordanArray[g_, f_]] := {g[#] &, f[#] &};
GetGeneratingFunctionPairs[
RiordanArray[g_, f_], {t_, n_Integer?NonNegative}] :=
{Series[g[t], {t, 0, n}], Series[f[t], {t, 0, n}]};
ASequence[RiordanArray[g_, f_]] :=
With[{finv = InverseFunction[f]}, (#/finv[#]) &]
ZSequence[RiordanArray[g_, f_]] :=
With[{zseq = (Values[
First@Solve[{z[
u] == (g[t] - SeriesCoefficient[g[t], {t, 0, 0}])/(t*
g[t]), u == f[t]}, z[u], {t}]] /. u -> #)[[1]]}, zseq &]
FindGeneratingFunctionPairs[ASequence_, ZSequence_, dinit_] :=
With[{sols =
Solve[Join[{(h[t]/t) == ASequence[h[t]], t > 0}, (# > 0) & /@
CoefficientList[ASequence[t], t]], h[t], Reals]},
With[{f = (Values[First@sols][[1]] /. t -> #) &},
g = (Values[
First@Solve[
Join[{d[t] == dinit*Power[1 - t*ZSequence[f[t]], -1],
t > 0}, (# > 0) & /@ CoefficientList[ZSequence[t], t]],
d[t], Reals]][[1]] /. t -> #) &;
RiordanArray[g, f]
]
]
NestTree[If[# == 0, {0, 0, 1}, {# - 1, # - 1, #, #, # + 1}] &,
RulesTree[0 -> {0, 0, 1}], 1];
treeRiordan =
FindGeneratingFunctionPairs[(\[Alpha] + \[Beta] # + \[Gamma] #^2) \
&, (\[Beta] + \[Gamma] #) &, 1];
{gTree, fTree} = GetGeneratingFunctionPairs[treeRiordan];
treeRiordanExample =
RiordanArray[(Simplify[
gTree[t] /. {\[Alpha] -> 1, \[Beta] -> 2, \[Gamma] -> 2},
t > 0] /. t -> #) &, (Simplify[
fTree[t] /. {\[Alpha] -> 1, \[Beta] -> 2, \[Gamma] -> 2},
t > 0] /. t -> #) &];
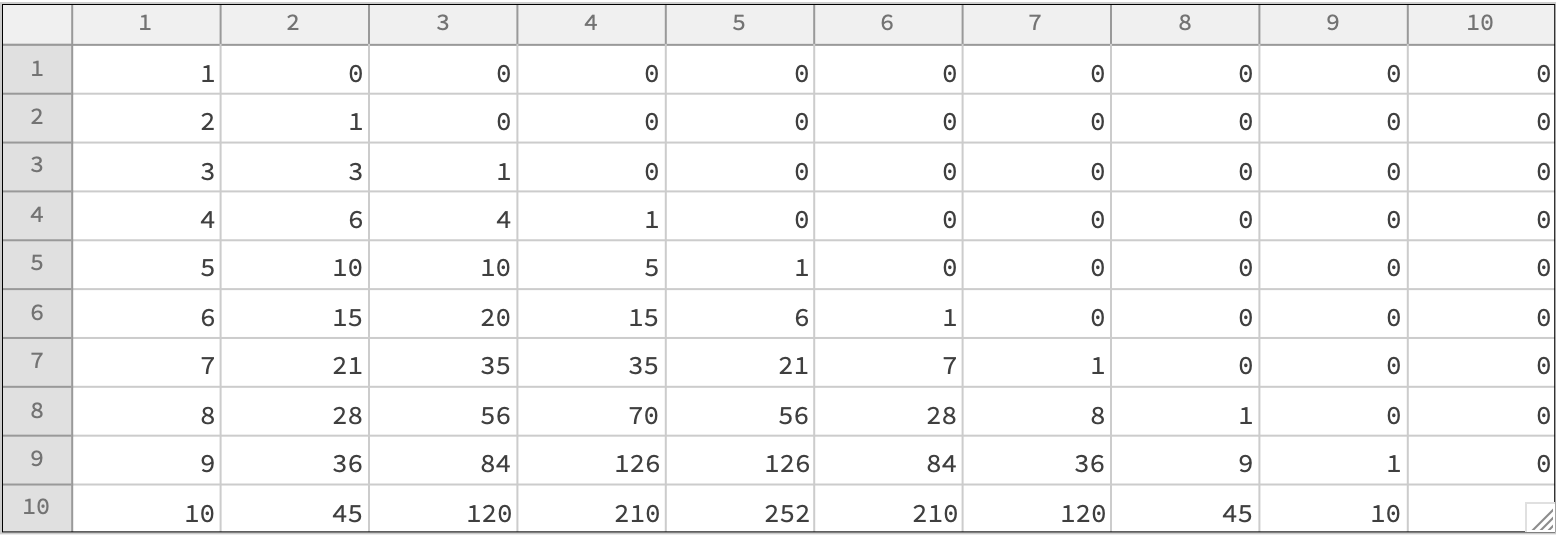
MatrixForm[treeRiordanExample, {0 ;; 10, 0 ;; 10}]
treeRiordanExample[0 ;; 10, 0 ;; 10]/
Dot[treeRiordanExample[0 ;; 10, 0 ;; 10],
ConstantArray[1, 11]] // MatrixForm
weights = Array[Factorial[#] &, 11, 0];
weightedTable =
Map[(weights*#) &, (treeRiordanExample[0 ;; 10, 0 ;; 10]/
Dot[treeRiordanExample[0 ;; 10, 0 ;; 10], weights])];
MatrixForm[weightedTable,
TableHeadings -> {Range[0, 10], Range[0, 10]}]
seriesCoefficients =
Table[SeriesCoefficient[
FTRA[treeRiordanExample, (1) &, k][t], {t, 0, n}], {n, 0, 9}]
ListLogPlot[{seriesCoefficients, Log[seriesCoefficients]},
PlotRange -> All, PlotTheme -> "Detailed", Frame -> True,
FrameLabel -> {"Coefficient index", "Coefficient value"},
PlotLabel ->
"Logarithmic series coefficients for FTRA of tree Riordan array"]
{gSeq, fSeq} =
GetGeneratingFunctionPairs[
FindGeneratingFunctionPairs[(1 + #) &, (1) &, 1]];
TableView@
Array[RiordanArray[(gSeq[t] /. t -> #) &, (fSeq[t] /.
t -> #) &], {10, 10}]
gSeq[t]
fSeq[t]
You could even use these Riordan arrays to model cockatoos, cockatoos are the smartest. That would really help us understand how the mathematical structure of the array provides insight into the behavior of the cockatoos over time.
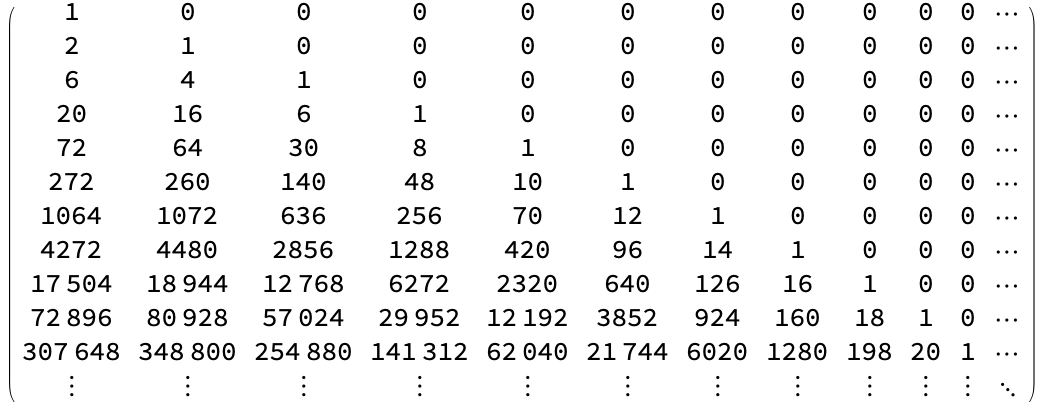
On what order of combinatorial enumeration of say lattice walks does your strategy acquire the acquaintance necessary to explain branchial space?

Or maybe we don't even need the computational efficiency to find a Riordan matrix but we can compute the normalization constant of a probability distribution.
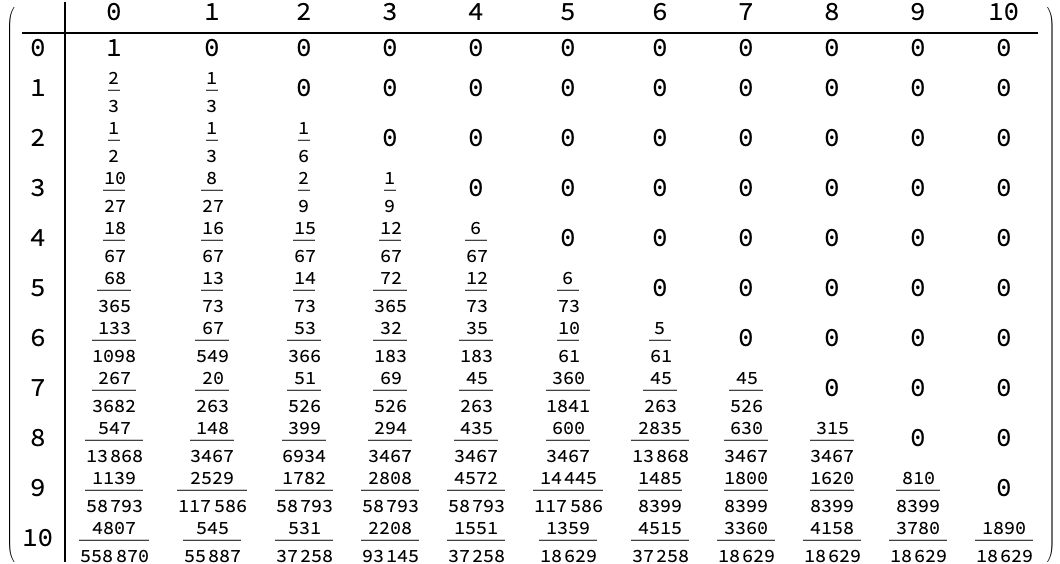
No matter what we can just do some multi-way systems, computational challenges of network partitioning NEAT.
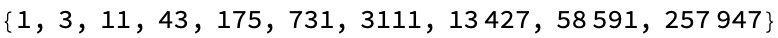
Could this Riordan array be used for blockchain? I genuinely just don't know what I'm talking about the topic is multi-way computation.
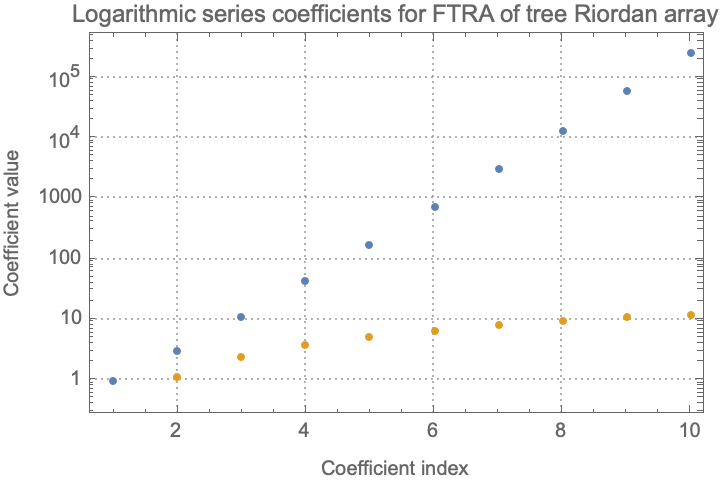
Suppose we've been in the process of sending all those green tokens, turquoise tokens, and we've got some hash functions and adjacency matrices...could we do a lattice walk to reach these terminal nodes across the Ruliad?
I wanted to take a moment to express my deepest gratitude @Jan Greve for your valuable contributions. My name is Dean and I enjoyed your insightful article on the Riordan array that really opened up new possibilities for me to explore and it is your dedication, to guiding me through the project that was truly inspiring, a promising new development in the field of combinatorics.
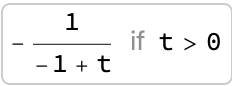
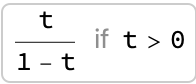
Your contributions have not gone unnoticed, and I am grateful to have had the opportunity to work with you and learn from you during the Wolfram Summer School.