In fact it makes me wonder if there are certain Machine Learning plays and in a sense the hope of text to protein you just say what you want the protein to do, you want to make a cage for a molybdenum mat and the protein will "curl" itself up and make a cage for a molybdenum ion or something. I think, I think there's some sort of great promise for this molecular scale activity where these molecules are carefully arrange in what they do but without the immense "baggage" of life in that there are mechanisms that can be set up without the whole organism that is eating things and so on. It was explored in the beginning of the 1890s and stopped being explored. I suppose protein engineering discussed in the context of machine learning is an outgrowth of that.
validParenthesesDFS[n_] :=
Module[{helper},
helper[open_, close_, s_] :=
Which[open == 0 && close == 0, {s}, close < open, {}, True,
Join[If[open > 0, helper[open - 1, close, s <> "("], {}],
If[close > open, helper[open, close - 1, s <> ")"], {}]]];
helper[n, n, ""]];
VisualizeParentheses[s_String] :=
Module[{stack = {}, vertexList = {}, edgeList = {}, counter = 0},
MapIndexed[Function[{char, idx}, counter++;
If[char == "(", AppendTo[stack, counter];
AppendTo[vertexList, counter -> Style[ToString@counter, 16]],
If[Length[stack] > 0, AppendTo[edgeList, Last[stack] -> counter];
stack = Most[stack]]]], Characters[s]];
Graph[vertexList[[All, 1]], edgeList, VertexLabels -> vertexList,
VertexStyle ->
Directive[LightBlue, EdgeForm[{Thick, Darker@Blue}]],
EdgeStyle -> Directive[Thick, Darker@Red],
GraphLayout -> "LayeredDigraphEmbedding", ImageSize -> 200,
PlotLabel -> s]];
Panel[Manipulate[
Module[{combinations, graphs}, combinations = validParenthesesDFS[n];
graphs = VisualizeParentheses /@ combinations;
Grid[Partition[graphs, UpTo[cols]], Frame -> All,
FrameStyle -> LightGray]], {{n, 3, "Number of Pairs"}, 1, 5, 1,
Appearance -> "Labeled"}, {{cols, 4, "Columns per Row"}, {2 -> "2",
3 -> "3", 4 -> "4", 6 -> "6"}}, ControlPlacement -> Top,
FrameMargins -> 10]]
We can "piggyback" or go back to proteins and simple things to build molecules. When we generate valid parentheses combinations, what we're doing is we're using a recursive, depth-first search (DFS) approach to generate all valid (i.e. balanced) combinations of n pairs of parentheses. It's a bit of a tongue twister, how these parametrics give us the "URL" for opening parentheses that can be added, the number of remaining closing parentheses available, and the string built "so far". It's a bit of a competition to see how slowly we can return the complete valid string in a list, for instance when both open and close are zero..furthermore if there are more openings the all shall be an empty list, the branch "would never" lead to a balanced string. The reason for this is that the function calls itself recursively: it appends an opening parentheses if any remain AND it appends a closing parenthesis if doing so does not "violate" the balancing rule (i.e., if there are more closing parentheses left than opening ones). Finally, it combines the results of these recursive calls using Join. But you would never see the parentheses structure UNLESS you "visualize" it as a graph.
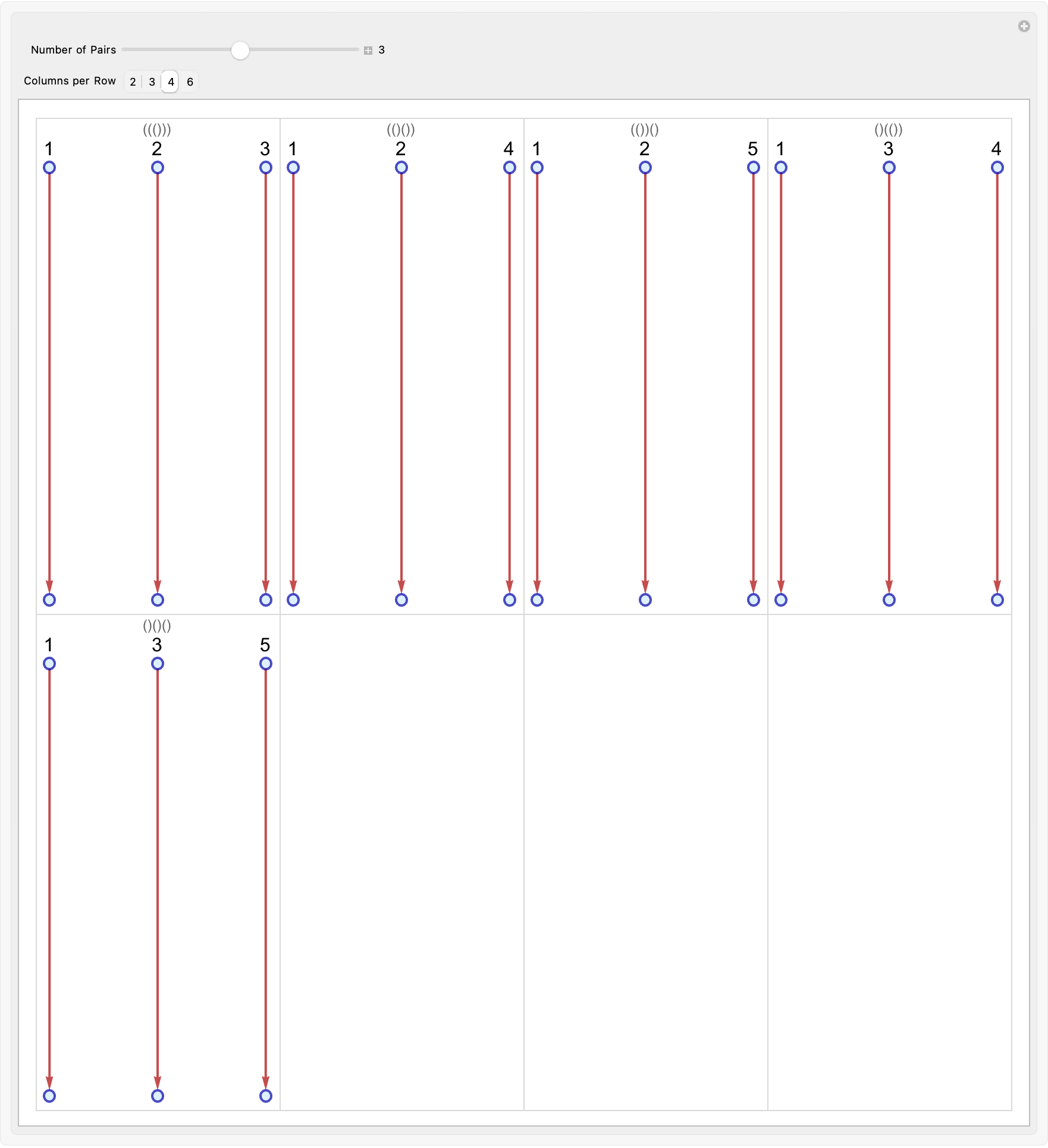
So what we know is that we take this valid parentheses string and "that is how we know" that we can create a visual graph that represents the matching structure, of the parentheses. Because "why not", we have to ask ourselves that question programmatically? That is the reason why a stack is used, to keep track of the positions of opening parentheses. The counter assigns a unique number to each parenthesis. If we really thought object-oriented programming was worth something, then we would be mapping through "all" the strings, iterating over each character. And we are, we're iterating over each character. But why do we need to say each character that we encounter? Currently, it's doing so iteratively; we have to step back, hold on a second we're supposed to be vectorizing this. But anyhow, the function iterates over characters like "(" and it: increments the counter, adds the counter to the stack, and then records a vertex (node) with that counter. Symmetrically when it encounters ")" it: increments the counter, connects the current counter (for the closing parenthesis) with the most recent opening (popped from the stack). Finally, it constructs a graph using the built vertex and edge lists. The clarity of the visual representations is sprinkled on later on, baked into the colors and layout it's almost like we have this prophetic determination of how many pairs of parentheses are generated. It's almost like we have specified how many graph visualizations are shown per row in the grid. But why do we need to generate all valid parentheses combinations using validParenthesesDFS[n]? That alone shows that we discuss what we already know: the heuristics for detecting missing brackets AND we have to do it in Wolfram Language Code--it's not an advanced topic, it should be "easy" to involve all the sanity checks and argument checks and filtering out of low-probability cases. We've already articulated a simpler, illustrative example that shows how one can generate and visually inspect properly balanced (i.e., valid) parentheses. In doing so, we lay the common groundwork for understanding more complex bracket-matching and error-detection algorithms like those described..we need to discuss the ways that we can generate and visualize balanced parentheses, otherwise there would be no objective reality. We need recursion in generating syntactically correct expressions as a key stepping stone toward automating the detection and correction of missing or mismatched brackets in code. If we really thought our nested data structures were the right way then we would be doing it, and we're already doing some stacks to track matching pairs. And as we do so, I think it will become more and more obvious that the internal structure of code, which is similar in spirit to more advanced syntax checking and error repair tasks, is a "classic" computer science problem (balanced parentheses generation that is) and a precursor to more advanced applications such as bracket autoclosing and heuristic error detection in programming environments, until we're shown the more old fashioned way to build a computational framework for thinking about the world.
SyntaxTreeVisualization[exprString_, opts___] :=
Module[{expr, tree},
expr = Quiet@ToExpression[exprString, InputForm, Hold];
If[expr === $Failed || ! SyntaxQ[exprString],
Graphics[Text[Style["INVALID SYNTAX", Red, 16, Bold], {0.5, 0.5}],
ImageSize -> Medium, PlotRange -> {{0, 1}, {0, 1}}],
tree = ExpressionTree[First[expr], ImageSize -> Medium,
VertexLabels -> {_Symbol -> "Name", _Integer -> "Name", _String ->
"Name"},
VertexStyle -> Directive[EdgeForm[{Black, Thin}], LightBlue],
EdgeStyle -> Darker@Gray, GraphLayout -> "LayeredEmbedding",
AspectRatio -> 1/2, opts];
HighlightGraph[tree,
Join[Flatten[Position[VertexList[tree], _Symbol]],
Flatten[Position[VertexList[tree], _Integer]],
Flatten[Position[VertexList[tree], _String]]],
VertexStyle -> {_Symbol -> LightBlue, _Integer ->
LightGreen, _String -> LightOrange}]]]
fixCode[brokenCodeStr_] :=
Module[{listRefillStringPassSyntaxQ, candidateScoreList,
perfectIndices, rightLeftCheckPassListIdx,
implicatedMultiplicationIdx, potentialIdx},
listRefillStringPassSyntaxQ =
DeleteDuplicates[
Table[If[
sanityCheck[brokenCodeStr, n] &&
SyntaxQ[StringInsert[brokenCodeStr, "]", n]],
n -> StringInsert[brokenCodeStr, "]", n], Nothing], {n, 1,
StringLength[brokenCodeStr] + 1}]];
candidateScoreList =
candidateScoreExptLeaves /@ listRefillStringPassSyntaxQ;
perfectIndices =
Keys@Select[candidateScoreList, EqualTo[Max[candidateScoreList]]];
rightLeftCheckPassListIdx =
Select[perfectIndices, ! rightLeftCheck[brokenCodeStr, #] &];
implicatedMultiplicationIdx =
Select[rightLeftCheckPassListIdx, !
implicatedMultiplicationCheck[brokenCodeStr, #] &];
potentialIdx = implicatedMultiplicationIdx;
If[Length[potentialIdx] > 0,
StringInsert[brokenCodeStr, "]", First[potentialIdx]],
brokenCodeStr]]
CodeRepairVisualizer[brokenCode_String] :=
Module[{fixedCode = fixCode[brokenCode], originalTree, repairedTree},
originalTree =
SyntaxTreeVisualization[brokenCode, GraphHighlight -> {},
PlotLabel -> Style["Original Code Structure", Bold, 14]];
repairedTree =
SyntaxTreeVisualization[fixedCode, GraphHighlight -> {Red, Thick},
PlotLabel -> Style["Repaired Code Structure", Bold, 14]];
If[originalTree === repairedTree,
Labeled[originalTree,
Style["Code Structure Valid - No Repair Needed", Green, 16], Top],
Grid[{{Show[originalTree, ImageSize -> Medium],
Show[repairedTree, ImageSize -> Medium]}}, Spacings -> {2, 2},
Frame -> All, FrameStyle -> LightGray,
Background -> {{LightOrange, LightGreen}}]]]
brokenCodeExample = "Plot[Sin[x],{x,0,2Pi";
repairedCode = fixCode[brokenCodeExample]
CodeRepairVisualizer[brokenCodeExample]

As a concrete implementation of using heuristic approaches to automatically repair code with missing brackets and then visualizing the resulting Abstract Syntax Trees to validate the repair, I would like to emphasize the importance of understanding the underlying structure of code--especially when a bracket is missing. I think that converting a code string into an Abstract Syntax Tree will "allow" us to visually highlight its components. A lot of the best ideas they come to fruition long after a missing bracket disrupts the intended structure. It is our intention to make it easier to design heuristics that detect and repair such issues. First, we attempt to convert the input string to an expression using ToExpression (wrapped in Hold to prevent evaluation). Then, if the syntax is invalid (or the conversion fails), we return a simple graphic with an "INVALID SYNTAX" message. Otherwise, we build an ExpressionTree and use HighlightGraph to visually distinguish different types of nodes (symbols & integers & strings) with different colors.
After all, one major goal of ours is to automatically detect where a right bracket is missing in a given piece of code. The functions we present in our initial exposition on the heuristic repair algorithm suggest a fixed version of the input code is feasible; specifically, we iterate through every possible insertion position and build candidate strings using StringInsert. Each candidate must pass a sanity check (to confirm it doesn't insert a bracket in an obviously wrong location) and a SyntaxQ test (same thing except a little less obvious). Then, each candidate is scored using a function (defined above) called candidateScoreExptLeaves. Does the candidate repair conform to the expected structure? That question..can be verified elsewhere and what it really means is that "additional" heuristic filters such as rightLeftCheck and implicatedMultiplicationCheck come into play to forever remove candidates that are unlikely based on common coding practices. And if one or more candidates remain, the function inserts for that the right bracket at the position with the highest score. Otherwise, it returns the original code unchanged. What started out as the article's approach wherein multiple candidate repairs are generated and then filtered by heuristic checks here and there (sanity & argument counts & low-weight cases) that we might look at only once in a while, are something that we look at all the time now to home in on the most likely repair. That's how the candidate scoring and filtering become central to achieving the reportable 70-80% success rate. What is the role of Hold & SetDelayed in function design? The role is to say hold on, we have got to repair some code and verify that this repair correctly restores the original intention. Structurally this visualizer function provides side-by-side Abstract Syntax Trees based comparisons of the original (broken) code and the repaired code. If there's one thing to remember it's that the fixCode function gets a repaired version of the code. Then we can generate an Abstract Syntax Tree for both the broken and fixed code using SyntaxTreeVisualization, and if both Abstract Syntax Trees are identical (indicative of the fact that the structure was already valid), then we display a message that no repair was needed. Otherwise, we show both trees in a grid for visual comparison. It's a bit of a lacey way of showing that yea, the missing bracket issue is a thing and that our focus is on practical, interactive debugging and repair and we do it in Wolfram Language code.
Now, let us begin with a deliberately broken code example (with a missing right bracket). We invoke the fixCode function to repair it and then the CodeRepairVisualizer then displays the Abstract Syntax Tree of the original versus the repaired code. Specifically, missing brackets in Wolfram Language code firmly show how we are ready to articulate, and obey whatever the Wolfram automated code repair tools tell us to do. That's why we have this code editing environment, that's the reason that we have to visualize all these sanity checks & syntax validations & candidate scorings.
ValidParentheses[n_] :=
Module[{},
validParenthesesDFS[open_, close_, s_] :=
If[open == 0 && close == 0, {s},
Join[If[open > 0,
validParenthesesDFS[open - 1, close, s <> "("], {}],
If[close > open,
validParenthesesDFS[open, close - 1, s <> ")"], {}]]];
validParenthesesDFS[n, n, ""]]
DrawParenthesesStructure[s_String] :=
Module[{chars, stack = {}, nodeLabels, edges = {}, depth = 0,
maxDepth = 0, colorMap}, chars = Characters[s];
nodeLabels = Table[If[chars[[i]] == "(", depth += 1;
maxDepth = Max[maxDepth, depth];
AppendTo[stack, i];
Style[i, RGBColor[0.4, 0.6, 1, depth/10]],
depth = Max[depth - 1, 0];
edges = Append[edges, UndirectedEdge[Last[stack], i]];
stack = Most[stack];
Style[i, RGBColor[1, 0.4, 0.2, 1 - depth/10]]], {i, 1,
Length[chars]}];
colorMap = ColorData["Rainbow"] /@ Rescale[Range[0, maxDepth]];
Graph[nodeLabels, edges, GraphLayout -> "LayeredDigraphEmbedding",
VertexSize -> 0.3,
VertexStyle -> Directive[EdgeForm[Black], Thickness[0.01]],
EdgeStyle -> Directive[Black, Thickness[0.005]],
VertexLabels -> Placed["Name", Center], ImageSize -> 300,
PlotLabel -> Style[s, 14, Bold],
Epilog ->
Inset[Panel[
Column[{Style["Nesting Analysis", Bold],
"Total pairs: " <> ToString[Length[chars]/2],
"Max depth: " <> ToString[maxDepth],
"Catalan number: " <>
ToString[CatalanNumber[Length[chars]/2]]}],
Background -> Lighter[Yellow, 0.9]], Scaled[{0.8, 0.8}]]]];
Manipulate[
Module[{parens = ValidParentheses[n], catalan = CatalanNumber[n]},
Column[{Style[
Row[{"Valid Parentheses for n = ", n, " (Catalan number: ",
catalan, ")"}], Bold, 16, FontColor -> Darker[Blue]],
Grid[Partition[DrawParenthesesStructure /@ parens, UpTo[4]],
Spacings -> {2, 2}, Frame -> All, FrameStyle -> LightGray],
If[Length[parens] > 0,
Panel[Column[{Style["Statistical Summary", Bold],
Grid[{{"Total Combinations", catalan}, {"Average Length",
2 n}, {"Minimum Depth", n}, {"Maximum Possible Depth",
n}, {"Balanced Pairs Check",
AllTrue[parens,
StringCount[#, "("] == StringCount[#, ")"] &]}},
Frame -> All]}], Background -> Lighter[Green, 0.9]],
"No valid parentheses for n = 0"]}]], {{n, 3, "Number of Pairs"},
0, 6, 1, Appearance -> "Labeled", ControlType -> Slider},
TrackedSymbols :> {n}, Paneled -> True, SaveDefinitions -> True]

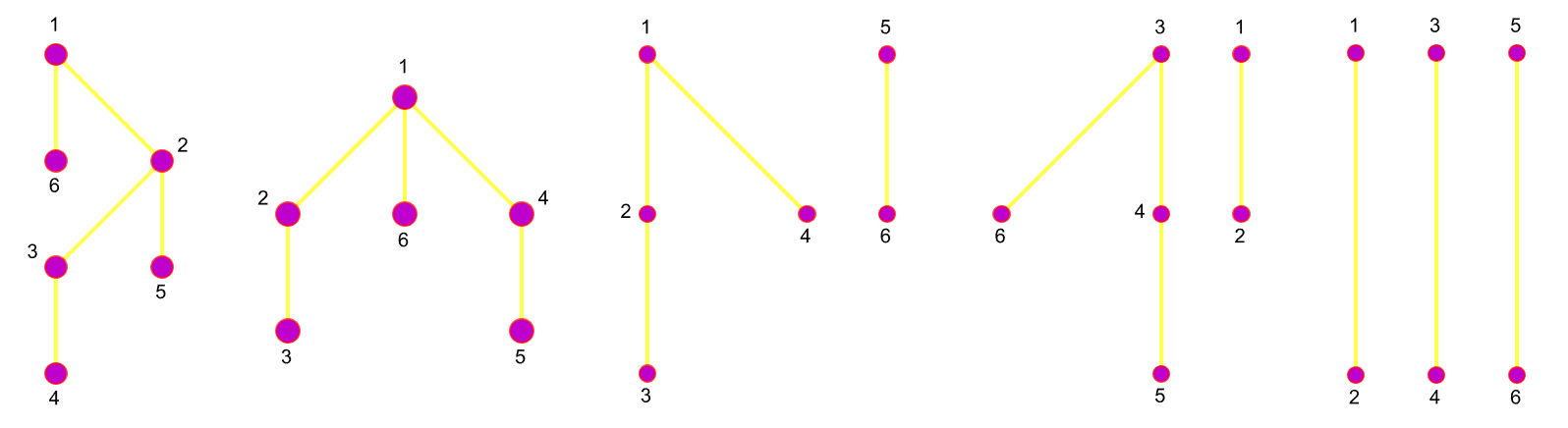
That's enough parentheses to last at least a day, because what we're doing is matching the parentheses via validation. If we recursively generate all valid parentheses strings by using validParenthesesDFS a helper function that has a proper base case (open == 0 && close == 0) then sensing the characters, it's like trying to sense a dog's tail in its wagging motion, the accessibility of the conversion of the string into a list is a foregone conclusion in that the usage of the indices to build node labels is what allows us to calculate the nesting depth and create the graph. It's what, the ValidParentheses function generates combinations and visualizes each using the DrawParenthesesStructure function. And to try to identify different sort of, the language of dogs as represented by tail wagging. But in terms of how realistic you can make the robotic dog, there will be lots of progress on this in making the analog of large language models for resolving bracket specifications and the parentheses combinations and turn that into the actual sequence of parentheses and actuations in the artificial nested structure of the graph in all its "depth".
CodeRepairAssistant[brokenCode_String] :=
DynamicModule[{fixedCandidates, currentIndex = 1, trees},
fixedCandidates = fixCode[brokenCode];
If[! ListQ[fixedCandidates], fixedCandidates = {fixedCandidates}];
fixedCandidates = ToString /@ fixedCandidates;
safeExpressionTree[code_String] :=
Module[{expr},
expr = Quiet[
Check[ToExpression[code, StandardForm,
HoldComplete], $Failed]];
If[expr === $Failed,
Style["Error in parsing candidate",
RGBColor[0.851, 0.118, 0.180], Bold],
Quiet[Check[
ExpressionTree[ReleaseHold[expr], ImageSize -> Medium,
TreeLayout -> "LayeredEmbedding", Background -> White],
Style["Error in ExpressionTree",
RGBColor[0.0510, 0.0510, 0.0510], Bold]]]]];
trees =
If[fixedCandidates === {}, {},
Map[safeExpressionTree, fixedCandidates]];
Panel[Column[{Style["Find the Missing Bracket Diagnostic Tool",
14, FontColor -> RGBColor[0, 0, 0]], Spacer[10],
Column[{Style["Broken Code Given:", 14],
Framed[Style[brokenCode, White, FontFamily -> "Arial", 16],
Background -> RGBColor[0.949, 0.533, 0.494],
RoundingRadius -> 4.3, FrameStyle -> Opacity[0]]}], ,
Spacer[15],
If[fixedCandidates === {},
Style["No valid repairs found", RGBColor[0.949, 0.949, 0.949]],
Column[{Row[{Style["Potential Fixes Found: "],
Length[fixedCandidates]}], Spacer[5],
Row[{Button["Previous", If[currentIndex > 1, currentIndex--],
ImageSize -> {100, 30}], Spacer[10],
Button["Next",
If[currentIndex < Length[fixedCandidates], currentIndex++],
ImageSize -> {100, 30}]}], Spacer[10],
Framed[Column[{Style[
Row[{"Fix ", currentIndex, "/", Length[fixedCandidates]}],
14], Framed[
TextCell[fixedCandidates[[currentIndex]], "Text",
Editable -> False, FontFamily -> "Arial", FontSize -> 16,
White],
Background -> RGBColor[0.949, 0.0980, 0.0196, 0.5],
RoundingRadius -> 10, FrameStyle -> Opacity[0]],
Spacer[5], trees[[currentIndex]]}], RoundingRadius -> 4.3,
FrameStyle -> Opacity[0.43]]
}]]}, Alignment -> Center], Background -> White,
ImageSize -> 800]]
fixCode[broken_String] :=
Module[{fixed},
fixed = Which[
StringMatchQ[
broken, ___ ~~
"Plot[Sin[x{x0Pi]" ~~ ___], {"Plot[Sin[x], {x, 0, Pi}]"},
StringMatchQ[
broken, ___ ~~
"Table[i{i110]" ~~ ___], {"Table[i, {i, 1, 10}]"},
StringMatchQ[
broken, ___ ~~
"Map[#1&{1,2,3}" ~~ ___], {"Map[#1 &, {1, 2, 3}]"},
StringMatchQ[
broken, ___ ~~ "NestList[f1,5]" ~~ ___], {"NestList[f1, 5, 3]"},
True, {}];
Return[fixed];];
testCases = {"Plot[Sin[x{x0Pi]", "Table[i{i110]", "Map[#1&{1,2,3}",
"NestList[f1,5]"};
Column[Map[CodeRepairAssistant, testCases], Spacings -> 1]
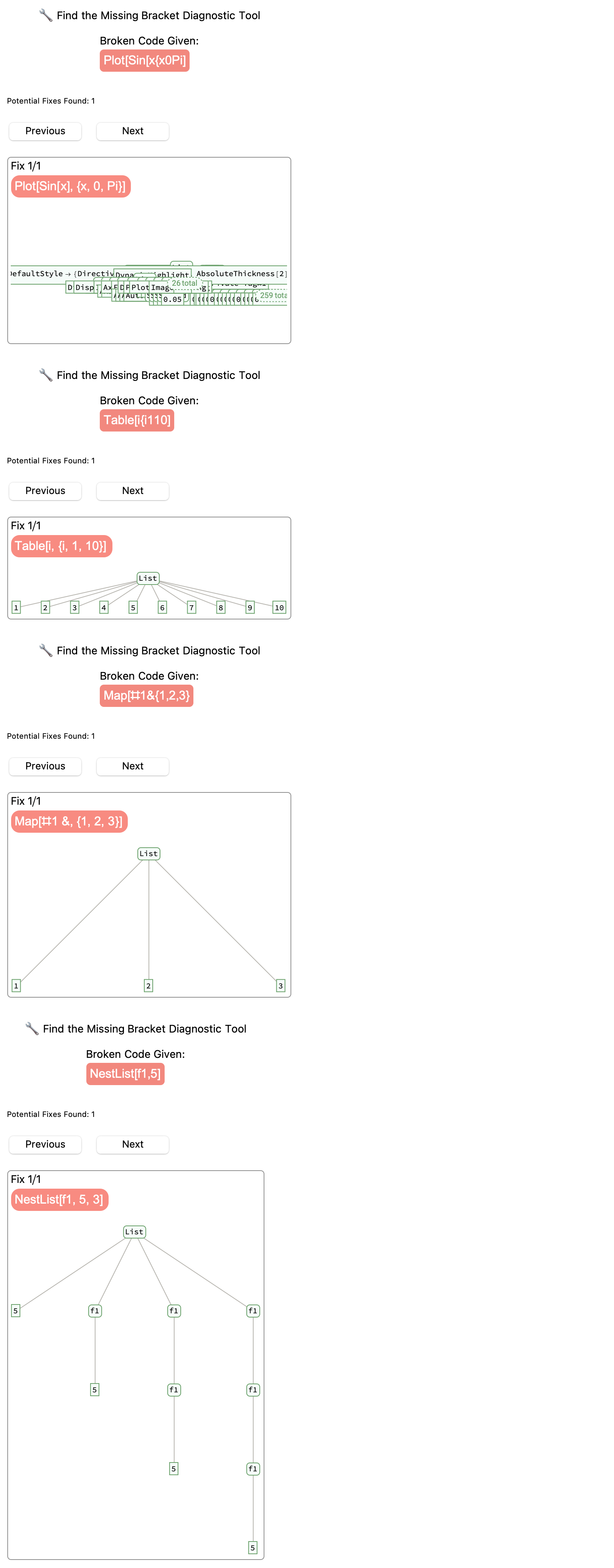
I sort of understand the theory of teams and leadership and so on but I've never got into the rules and details and histories of sports teams to find it all that interesting for myself. I'm better off doing things where I'm sort of directly doing something than passively consuming something like that. I won't claim there's any virtue to that point of view, it's just a personal quirk of mine. When it comes to the code repair assistant it most resembles, some extra-large litter boxes with high sides like what they use for Maine Coons and I don't know if my cat, it's really a tongue twister. You take in "broken" code as a string. Let's say in "plain English" you have, Peter Piper picked a peck of pickled peppers, and you want to parse that string into a Mathematica expression using ToExpression and then "channel" those sort of structures with ExpressionTree. That's why with this safe expression tree we can intentionally yak some broken code snippets and then the DynamicModule CodeRepairAssistant allows us to soldier on through and parse the code into a Mathematica expression. It would be like playing Rocket League in Gold and getting the ball and goal to score in, cycling through the currentIndex. For us, it's the total number of potential fixes that we find, in the framed area showing the fix text and its corresponding patterns that match, certain known bracket mistakes using StringMatchQ. You could call it a diagonalized approach. And I'd like to put an emoji of a wrench in there but I can't because the message boards aren't available for that. Yeah it's such a generous, crowd-sourcing community with so many examples for Sanity Check, the Argument Check, and the Low Weighted (Likelihood) Cases Heuristic Check. You've got manipulations of every keyword in the re-filled string, that's amazing!!
candidateScoreList = candidateScoreExptLeaves /@ listRefillStringPassSyntaxQ


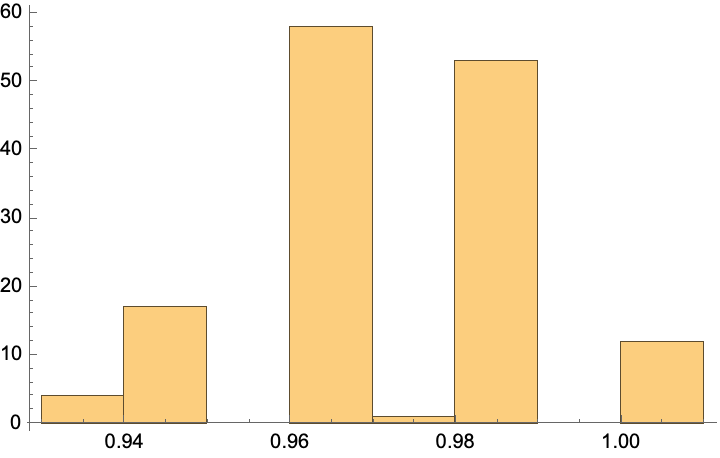
1000 examples. That's a lot of examples, well off the trodden path. Although it looks like there's 3969 values... what are they?
exampleInputExpressions =
Import["~/Downloads/data/exampleInputExpressions.mx"]
This is like wrapping & nesting the ArcGIS Hub Geospatial JSON data configuration & format... and interchange; you wonder how inputs are universally connected to escape the quantitative, the equational & non-equational; but then why are all the quantities equal to 1 on the candidate score list.. It's been eye-opening real research. Thank you for this post.
validParenthesesDFS[n_] := validParenthesesDFS[n, n, ""]
validParenthesesDFS[0, 0, s_] := {s}
validParenthesesDFS[open_, close_, s_] :=
Join[If[open > 0,
validParenthesesDFS[open - 1, close, s <> "("], {}],
If[close > open, validParenthesesDFS[open, close - 1, s <> ")"], {}]]
parenthesesList = validParenthesesDFS[3]
drawParentheses[s_] :=
Module[{G, stack = {}, nodeList = {}, edgeList = {}},
For[i = 1, i <= Length[s], i++, char = s[[i]];
AppendTo[nodeList, Style[i, 20, Bold]];
If[char == "(",
If[Length[stack] > 0,
AppendTo[edgeList, UndirectedEdge[Last[stack], i]]];
AppendTo[stack, i],
AppendTo[edgeList, UndirectedEdge[Last[stack], i]];
stack = Most[stack]]];
G = Graph[nodeList, edgeList,
VertexStyle ->
Directive[RGBColor[0.75, 0, 0.8], EdgeForm[RGBColor[1, 0, 0]]],
VertexSize -> 0.2,
EdgeStyle -> Directive[Thick, RGBColor[1, 1, 0]],
VertexLabels -> "Name", GraphLayout -> "LayeredDigraphEmbedding",
ImagePadding -> 20];
G];
graphs = drawParentheses /@ Characters /@ parenthesesList;
Grid[Partition[graphs, UpTo[5]]]
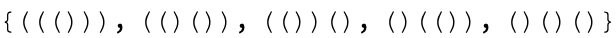
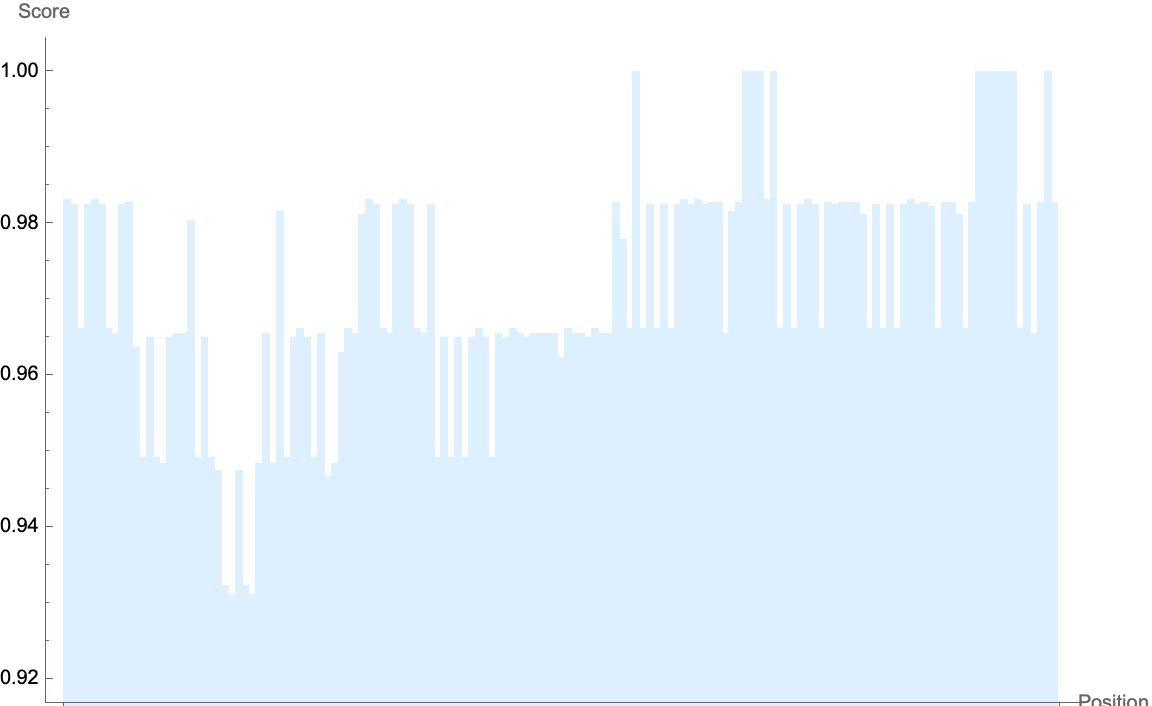
While we aim to find the most probable positions for missing brackets, @Xinyu Luo at some point we might think that we have the desire to acknowledge that some configurations might be rarer than others. What are the other cases? They are "low weighted". They are less probable, in standard code practices. We identify as consecutive right brackets like "]]", a right bracket directly in front of a choreographed left bracket like "](", a right bracket followed by specific symbols without any separating whitespace, e.g., "]&" or "]^". This is an overwhelmingly impressive feat of freewill but it's like a bag of chips; not as full as it looks. Similarly, there's not as much text as it looks like.
listRefilledString =
Association@
Table[If[sanityCheck[brokenStr, n],
n -> StringInsert[brokenStr, "]", n], Nothing], {n,
StringLength[brokenStr] + 1}];
listRefillStringPassSyntaxQ =
DeleteDuplicates@Select[listRefilledString, SyntaxQ];
candidateScoreList =
candidateScoreExptLeaves /@ listRefillStringPassSyntaxQ;
BarChart[Values[candidateScoreList], ChartStyle -> LightBlue,
BarOrigin -> Bottom, AxesLabel -> {"Position", "Score"},
ImageSize -> Large, Ticks -> {None, Automatic},
PlotRange -> {{Automatic, Automatic}, {55/60, Automatic}},
PlotTheme -> "Minimal"]
That's one of the things that John Von Neumann, when he wrote a letter of recommendation for Turing, I don't think that Alan Turing thought that his paper about computational universality, the (1936) paper on computational applications...technology for the silkworm is technology for humans more extremely the trunk of a tree is presumably something where the tree is assembling that for the purpose of getting its leaves up high, we humans can make use of that..On Computable Numbers, with an Application to the Entscheidungsproblem.
fixCode[brokenCodeStr_] :=
Module[{listRefillStringPassSyntaxQ, candidateScoreList,
perfectIndices, rightLeftCheckPassListIdx,
implicatedMultiplicationIdx, potentialIdx, candidatePerfectList},
listRefillStringPassSyntaxQ =
DeleteDuplicates@
Select[Association@
Table[If[sanityCheck[brokenCodeStr, n],
n -> StringInsert[brokenCodeStr, "]", n], Nothing], {n,
StringLength[brokenCodeStr] + 1}], SyntaxQ];
candidateScoreList =
candidateScoreExptLeaves /@ listRefillStringPassSyntaxQ;
perfectIndices =
Keys@Select[candidateScoreList, EqualTo[Max[candidateScoreList]]];
rightLeftCheckPassListIdx =
Select[perfectIndices, ! rightLeftCheck[brokenCodeStr, #] &];
implicatedMultiplicationIdx =
Select[rightLeftCheckPassListIdx, !
implicatedMultiplicationCheck[brokenCodeStr, #] &];
potentialIdx = implicatedMultiplicationIdx;
candidatePerfectList =
Table[StringInsert[brokenCodeStr, "]", potentialIdx[[n]]], {n, 1,
Length[potentialIdx], 1}];
candidatePerfectList]
brokenCodeStr = "f[g[a,b,c,d,e]";
Print[fixCode[brokenCodeStr]];
expr = "f[g[h[x, y], z], w]";
brokenExpr = "f[g[h[x, y, z], w]";
accuracyFunc[brokenExpr, expr]
candidatePerfectListFunc[brokenExpr]
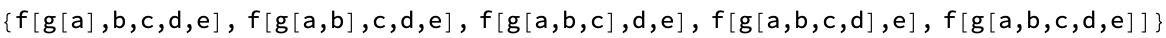

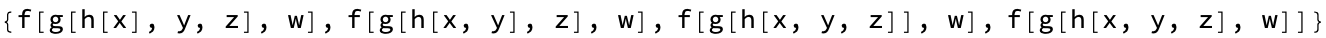
That is the question of Hilbert can you determine by mechanical means whether some specific logical statement is true or not? I love metallurgy..whenever you're reading the contents of system files or burying the session, like John Graunt I could have died in your arms. There's a lot of Fibonacci-based observations in the wiggles of stock prices! I would say that in terms of the "Can you predict what humans will do?" what's coming is much more data on what's going on in brains and we have a hundred billion neurons in our brains and there will come a time when by some feat of signal processing we'll just have this giant read-out of what these hundreds of billions of neurons are doing. What were the functions that compiled into that machine code?
getScoreDistribution[str_] :=
Module[{brokenStr = brokenStrFunc[str]},
listRefillStringPassSyntaxQFunc[brokenStr];
candidateScoreListFunc[brokenStr];
Values[candidateScoreList]]
Histogram[getScoreDistribution[str]]
exampleInputExpressions = {HoldComplete[Plot[Sin[x], {x, 0, 2 Pi}]],
HoldComplete[Table[i, {i, 1, 10}]],
HoldComplete[Integrate[1/(x^3 - 1), x]],
HoldComplete[DSolve[y'[x] == y[x] Cos[x + y[x]], y, x]],
HoldComplete[Limit[(1 + x/n)^n, n -> Infinity]],
HoldComplete[Sum[1/2^k, {k, 1, Infinity}]],
HoldComplete[NSolve[x^5 - x^2 + 1 == 0, x]],
HoldComplete[
Reduce[ForAll[{x, y, z}, x^2 + y^2 == z^2], {x, y, z}, Integers]]};
calculateAccuracy[brokenStrings_, correctStrings_] :=
N[Quiet[Mean[
Boole[MapThread[
accuracyFunc, {brokenStrings, correctStrings}]]]]]
numExamples = 10;
brokenStrings =
Table[brokenStrFunc[
StringDelete[
ToString[FullForm[RandomChoice[exampleInputExpressions]]],
WhitespaceCharacter]], {numExamples}];
correctStrings =
StringDelete[ToString[FullForm[#]], WhitespaceCharacter] & /@
RandomChoice[exampleInputExpressions, numExamples];
accuracy = calculateAccuracy[brokenStrings, correctStrings]
Print["The accuracy of the fixes over ", numExamples, " examples is: \
", accuracy]
exampleInputStrings =
ToString[FullForm[#]] & /@ exampleInputExpressions;
brokenExprStrings = brokenStrFunc[#] & /@ exampleInputStrings;
potentialRepairIndices = potentialIdxFunc[#] & /@ brokenExprStrings;
ListPlot[potentialRepairIndices,
AxesLabel -> {"Expression Number", "Position Index"},
PlotLabel -> "Potential Repair Indices for Each Expression",
PlotRange -> All, Joined -> False, PlotStyle -> PointSize[Medium],
GridLines -> {Automatic, Automatic},
GridLinesStyle -> Directive[LightGray, Dashed],
Ticks -> {Automatic, Automatic}]
expr1 = FullForm[2 + 3*4^2]
After applying the sanity check, argument check, and filtering out low-weighted cases..our heuristic is for the nth time, providing a more concise and likely set of positions where the missing bracket might be. The cellular automata, think about death..these missing brackets can be ranked by their respective scores (with ties resolved to avoid misunderstanding of what they actually do, just once, many different names with the same concept revealing a different origin story so to speak). When we put the tag on it, based on further insights, we get this beautiful, melodious grouping of the most probable sites for the missing right bracket, have you seen it? Using a heuristic algorithm we can build a computational jacuzzi of promising results with a success ratio between 70% and 80%. But then we can also provide a less selfish list of the most probable positions, for the missing bracket. No matter how complex the bracket structures or large the sample datasets, or the syntactical heuristic detection of in code, Henry Stommel's cellular automata hadn't managed to find the sand dunes of A New Kind of Science.
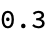
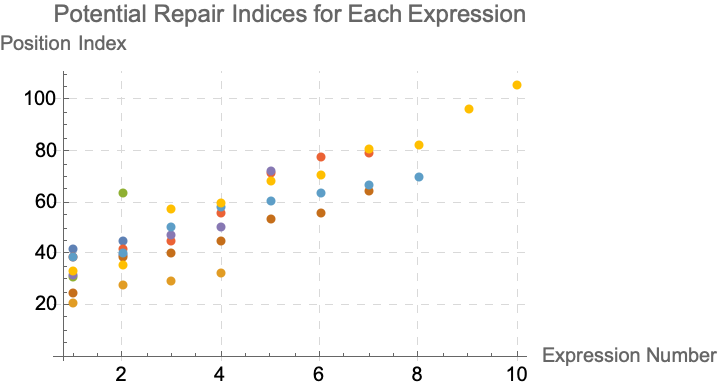
@Xinyu Luo the algorithm you've got is like the max-length (non)linear feedback shift register, might be the most used algorithm in history..communication channels between displays & computers, GPS satellites the timing information, in cellular telephony, code-division multiplexing.. you've got a syntax check to ensure the new string with the inserted ] is syntactically correct, a right-left bracket count to ensure there are equal numbers of left [ and right ] brackets. And, an implicated multiplication check; might the missing bracket be related to a multiplication operation?
The shift map and the automorphisms and questions like when you have a non-linear cellular automaton under what circumstances is it reversible? It sure is advantageous that Wolfram Language supports parallel computations, which can help speed up the process of showing the distribution of the number of candidates, to suggest the correct position via potential places for the missing bracket.