Message Boards Message Boards

0
|
9400 Views
|
8 Replies
|
0 Total Likes
View groups...
Share
Share this post:

Problem with constructing a function - Module inside a Manipulate

Petar M
Posted 11 years ago
I have an assignment to model a planetary revolution around the Sun, and to examine under which rotational speed will it leave orbit. The exact solution works, numerical also, but the problem arises when I try to put numerical sequence under Module command, and name it as one function in order of putting this function later on under "Manipulate" command in order to have a smooth way of examining the changes in the orbit arrising from changing the initial rotation speed.

So the code is basically ok, but what I don't know is how to put my numerical sequence under "Module" command in order to create a simple function that can be subjected to "Manipulate" command.
Is there someone that can help me with this?

I've attached the file with the problem.

Thanks
Attachments:
POSTED BY: Petar M
8 Replies
Sort By:
Petar M
Petar M
Posted 11 years ago

I have just seen your last posts. I noticed the same thing few days ago, but I already singed the paper. Not to worry it was alright since I didn't use manipulate, nobody (not even me till I increased the time frame), noticed that it makes these unstable orbits for small values. I also managed to solve on my own this thing with 1, -1, I thought you won't answer anymore, still thanks for your effort.

I would ask you if you could check one other of my posts. It concerns my last assignment. I have to interpret some code from wolfram demonstrations, but I am having troubles with it and I was wondering is there any explanation from the authors anywhere or some link that I could find literature that would explain this specific problem.

The link to my post is http://community.wolfram.com/groups/-/m/t/291006?p_p_auth=3MDolqmY

A comment from you would do good.

By the way what is your profession, I mean since you obviously know this stuff are you a programer or something like that?

Thanks once more, your help was of a great use.
POSTED BY: Petar M
But there is still this thing with moving from 1 to -1, don't know what is happening.
Look at
Clear[rorb]
rorb[vy0_ /; Chop[vy0] != 0, \[CurlyPhi]_] := (vy0 x0 - vx0 y0)^2/(
  4 \[Pi]^2)/(1 + Sqrt[1 + 2 ((vx0^2 + vy0^2)/2 - (4 \[Pi]^2)/r0) (vy0 x0 -
        vx0 y0)^2/(4 \[Pi]^2)^2] Cos[\[CurlyPhi] - \[Pi]]);

rorb[vy0_ /; Chop[vy0] == 0, \[CurlyPhi]_] := 1

for CurlyPhi = 0 fixed. Then Cos[CurlyPhi - Pi]= -1. With the numeric values you fixed the radicand is zero for vy0 = 2 Pi, the radikand is 1 for vy0 = 8.88577
In[108]:= Clear[vy0]
FindRoot[1 +  2 ((vx0^2 + vy0^2)/2 - (4 \[Pi]^2)/r0) (vy0 x0 - vx0 y0)^2/(4 \[Pi]^2)^2 == 1, {vy0, 8.8}]
Out[109]= {vy0 -> 8.88577}
and this is a singularity for rorb.

In[110]:= With[{vy0 = 8.88577, \[CurlyPhi] = 0},
{rorb[vy0, \[CurlyPhi]] Cos[\[CurlyPhi]],  rorb[vy0, \[CurlyPhi]] Sin[\[CurlyPhi]]} // N
]
Out[110]= {-1.07741*10^6, 0.}

Usually a singularity shows a point of the border of the definition area. Applying a formula outside of the definition area gives meaningless results.
POSTED BY: Udo Krause
I wanted to implemnt EC function in Manipulate command but from some reason it woun't do it just says abrted whent I try  
Manipulate[EC[vy0], {vy0, 0, 10}] 

that works (one has to wait for the picture because of the big nt)
POSTED BY: Udo Krause
Have you seen this
POSTED BY: Udo Krause
Petar M
Petar M
Posted 11 years ago
Thanks once again.

I am just a student of physics, and on my own on this one to add. So this help really means much. The chop part works, no errors anymore. But there is still this thing with moving from 1 to -1, don't know what is happening. The simulation should always start from one, since planet is one Astronomical unit away from the Sun, and then at one point when the starting rotational speed becomes too great it should leave the orbit, through hyperbole. Numerical solutions shows this nicely but the exact one has problems since like I said at one moment the elipse goes no more through 1 but through -1, and 1 should always be the starting point. Maybe chop again and than inverting sign of variables ?

Also just one more question concerning numerical solution. I wanted to implemnt EC function in Manipulate command but from some reason it woun't do it just says abrted whent I try

Manipulate[EC[vy0], {vy0, 0, 10}]

Once again thank you did so much allready I will understand if you don't answer this time. If there is any way to repay...
POSTED BY: Petar M
Because of
(* old rorb *)
In[7]:= Limit[rorb[X, 0], X -> 0, Direction -> 1]
Out[7]= 1

In[8]:= Limit[rorb[X, 0], X -> 0, Direction -> -1]
Out[8]= 1

one can say

 (* new rorb *)
 In[12]:= Clear[rorb]
 
 rorb[vy0_ /; Chop[vy0] != 0, \[CurlyPhi]_] := (vy0 x0 - vx0 y0)^2/(
   4 \[Pi]^2)/(1 + Sqrt[1 + 2 ((vx0^2 + vy0^2)/2 - (4 \[Pi]^2)/r0) (vy0 x0 -
         vx0 y0)^2/(4 \[Pi]^2)^2] Cos[\[CurlyPhi] - \[Pi]]);
 
 rorb[vy0_ /; Chop[vy0] == 0, \[CurlyPhi]_] := 1
 
In[16]:= rorb[0, 0]
Out[16]= 1
then the Manipulate[] is free of error messages, but it'sprobably still not free of errors:

It's switching between vy0 = 8.88 and  vy0 = 8.89, but a hyperbole is not visible, for 8.88 the abscissa runs from 0 to nearly 800, for vy0 = 8.89 the abscissa runs from about -1000000 to 0, here the code seemingly runs through a singularity, which needs either graphical care to catch the whole picture or analytical care to get the limits right. You are the theoretician of that: go ahead!

A propos, you can have more than one definition for a symbol like rorb[] in Mma: The main flavours for delayed functions, let's say f, are
f[x_<Type>?Test]:= <operations>
f[x_<Type>?Test /; Conditions]:= <operations>
f[x_<Type>?Test] := <operations> /; Conditions
Type and Test as well as Conditions can be omitted, there are many more possibilities (pure functions, functions with an indefinite number of arguments ...) all this can be cleared by
Clear[f]

and viewed by
?f
??f
Definition[f]
FullDefinition[f]

Think about a Mma function like f primarily as of a symbol. The symbol can be the target of different - preferably consistent -  definitions; because Mma is an infinite evaluation machine (it tries to apply as much transformation rules as it knows as long as the expression still changes) this gives you considerable freedom in stating functions. A function in Mma is by no means a [url=http://en.wikipedia.org/wiki/Function_(mathematics)]function in the strict mathematical sense, but it can be defined (by the user) to become a function or to behave like a function in the strict mathematical sense. This is up to you. One last thing, with
f[x_Integer, y_Integer, z_Integer:-1]

you can give e.g. the z argument a default value (-1) and call this symbol f as
f[x,y]
acting in fact as
f[x,y,-1]
POSTED BY: Udo Krause
Petar M
Petar M
Posted 11 years ago
Thank you so much.

Your advices are of great help.
If it is not to much I would ask one more question, how can I define the limit for rorb[0,0] and if I do that will that eliminate the mistake that it makes, to be concrete about it, it should make an elipse on the grafic that always goes through 1, and at one moment turns hyperbole, but this does not happen, it simply moves from 1 to minus 1 and than forms a hyperbole?

Again sorry if it is to much of a drag for you, I'll try to do this limit defining on my own but I am not sure will I know how.
And really thanks once again.
POSTED BY: Petar M
As a starter
In[14]:= rorb[X, 0]
Out[14]= X^2/(4 \[Pi]^2 (1 - Sqrt[1 + (X^2 (-4 \[Pi]^2 + X^2/2))/(8 \[Pi]^4)]))

from which one sees, that rorb[0,0] seems to be indeterminate (0/0) but the numerator vanishs with second oder, the denominator vanishes with first order, so L'Hospital would mean rorb[0,0]=1
In[15]:= Limit[rorb[X, 0], X -> 0]
Out[15]= 1

but Mma says
In[16]:= rorb[0, 0]
During evaluation of In[16]:= Power::infy: Infinite expression 1/0 encountered. >>
During evaluation of In[16]:= Infinity::indet: Indeterminate expression (0 ComplexInfinity)/(4 \[Pi]^2) encountered. >>
Out[16]= Indeterminate

one could easily fix that by defining rorb[0,0] to the correct limit.In either case this
 Manipulate[
  ParametricPlot[{rorb[vy0, \[CurlyPhi]] Cos[\[CurlyPhi]],
    rorb[vy0, \[CurlyPhi]] Sin[\[CurlyPhi]]}, {\[CurlyPhi], 0,
    2 \[Pi]}, PlotStyle -> Black, AspectRatio -> Automatic,
   FrameLabel -> {"\!\(\*
 StyleBox[\"x\",\nFontFamily->\"cmmi12\",\nFontSize->14,\nFontWeight\
 ->\"Plain\",\nFontSlant->\"Italic\",\n\
 FontVariations->{\"CompatibilityType\"->0}]\)\!\(\*
 StyleBox[
StyleBox[
RowBox[{
StyleBox[\" \",\nFontFamily->\"cmmi12\"],
StyleBox[\" \",\nFontFamily->\"Arial Narrow\"]}]],\nFontSize->14,\n\
FontWeight->\"Plain\",\nFontVariations->{\"CompatibilityType\"->0}]\)\
\!\(\*
StyleBox[\"[\",\nFontFamily->\"Arial Narrow\",\nFontSize->12,\n\
FontWeight->\"Plain\",\nFontVariations->{\"CompatibilityType\"->0}]\)\
\!\(\*
StyleBox[\"AU\",\nFontFamily->\"Arial Narrow\",\nFontSize->12,\n\
FontWeight->\"Plain\",\nFontVariations->{\"CompatibilityType\"->0}]\)\
\!\(\*
StyleBox[\"]\",\nFontFamily->\"Arial Narrow\",\nFontSize->12,\n\
FontWeight->\"Plain\",\n\
FontVariations->{\"CompatibilityType\"->0}]\)", "\!\(\*
StyleBox[\"y\",\nFontFamily->\"cmmi12\",\nFontSize->14,\nFontWeight\
->\"Plain\",\nFontSlant->\"Italic\",\n\
FontVariations->{\"CompatibilityType\"->0}]\)\!\(\*
StyleBox[\" \",\nFontFamily->\"cmmi12\",\nFontSize->14,\nFontWeight\
->\"Plain\",\nFontVariations->{\"CompatibilityType\"->0}]\)\!\(\*
StyleBox[\"[\",\nFontFamily->\"Arial Narrow\",\nFontSize->12,\n\
FontWeight->\"Plain\",\nFontVariations->{\"CompatibilityType\"->0}]\)\
\!\(\*
StyleBox[\"AU\",\nFontFamily->\"Arial Narrow\",\nFontSize->12,\n\
FontWeight->\"Plain\",\nFontVariations->{\"CompatibilityType\"->0}]\)\
\!\(\*
StyleBox[\"]\",\nFontFamily->\"Arial Narrow\",\nFontSize->12,\n\
FontWeight->\"Plain\",\n\
FontVariations->{\"CompatibilityType\"->0}]\)"}, PlotRange -> All,
  PlotLabel -> "Elipti?na orbita, egzaktno"], {vy0, 0, 20,
  Appearance -> "Labeled"}]
starts with an error without taking care about the limit.

Now about the EC[vy_] thing: that will not work because - as the error message states - the iterator for the Do[..., {i,nt}] has no upper limit nt, nt is a module local variable and is not set inside the Module[]. You have set it before the module, but the Module EC
 Euler - Cromerov metod
 x0 = 1.; y0 = 0.; vx0 = 0.; vy0 = 2 \[Pi]; t0 = 0.; tf = 10.;
 r0 = Sqrt[x0^2 + y0^2]; v02 = vx0^2 + vy0^2; e0 = v02/2 - (4 \[Pi]^2)/r0;
 l0 = vy0 x0 - vx0 y0;
 nt = 100000; dt = (tf - t0)/nt;
 tt = {t0}; xx = {x0}; yy = {y0}; ee = {e0}; ll = {l0};
 t = t0; x = x0; y = y0; vx = vx0; vy = vy0;
 
 EC[vy_] :=  Module[{vx, x, dt, r, y, t, xx, yy, tt, v2, e, ee, ll, l, i, nt},
  Do[(<snip> ....];

has all this variables as local entities, see Module, the fix is to initialize that local variables to the values you want.

Then there is another error, defining EC[vy_] you cannot assign another value to vy! Starting EC[2 Pi] you say vy = 2 Pi and then vy = vy - (4 \^2*y*dt)/r^3 means to assign 2 Pi to become something different from 2 Pi - forbidden with very sound reason. Use another name for the input, e.g. EC[vy0_] then it works and gives this picture



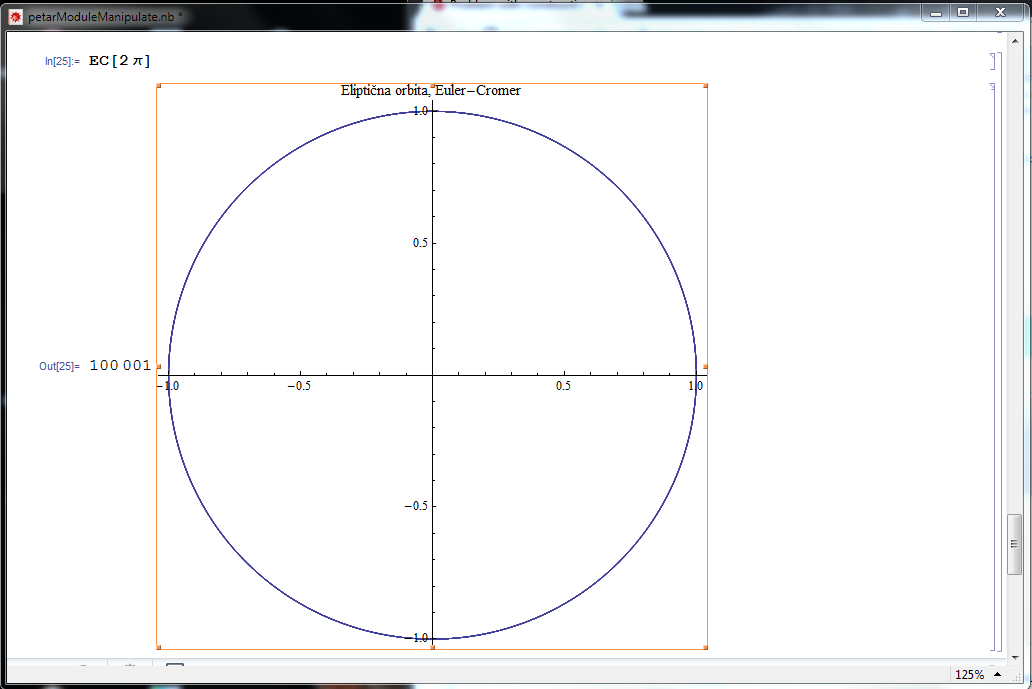
last but not least find please my modifications - which should be checked against further errors - in the appendix
Attachments:
POSTED BY: Udo Krause
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract