I noticed the following question here:

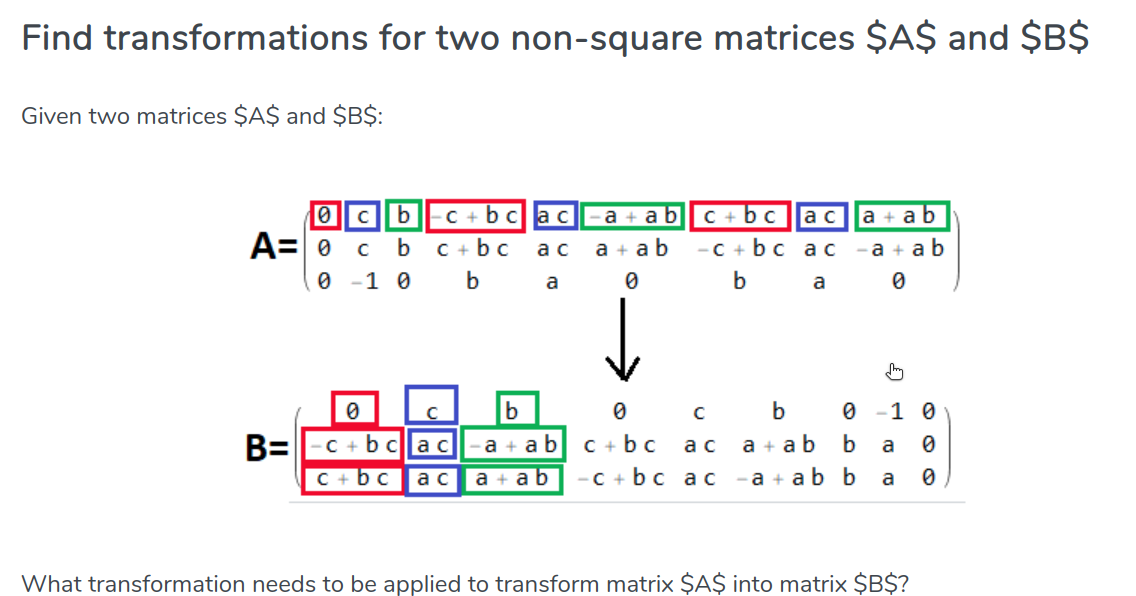
In[1]:= A = {{0, c, b, -c + b c, a c, -a + a b, c + b c, a c, 
   a + a b}, {0, c, b, c + b c, a c, a + a b, -c + b c, 
   a c, -a + a b}, {0, -1, 0, b, a, 0, b, a, 0}}

B = {{0, c, b, 0, c, b, 0, -1, 0}, {-c + b c, a c, -a + a b, c + b c, 
    a c, a + a b, b, a, 0}, {c + b c, a c, a + a b, -c + b c, 
    a c, -a + a b, b, a, 0}};

Out[1]= {{0, c, b, -c + b c, a c, -a + a b, c + b c, a c, 
  a + a b}, {0, c, b, c + b c, a c, a + a b, -c + b c, 
  a c, -a + a b}, {0, -1, 0, b, a, 0, b, a, 0}}

I also noticed the example code given on the same website as follows, which does not seem to be the solution to this problem and is very lengthy:

In[15]:= Rx = RotationMatrix[\[Phi][t], {1, 0, 0}];

Ry = RotationMatrix[\[Xi][t], {0, 1, 0}];

Rz = RotationMatrix[\[Psi][t], {0, 0, 1}];

Q = Rz . Ry . Rx;

v = {\[Phi][t], \[Xi][t], \[Psi][t]};

T1 = Flatten /@ D[Q, {v}];

T2 = Flatten /@ D[Transpose[Q], {v}];

P1 = {{1, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 1, 0, 0, 0, 0, 0}, {0, 0,
     0, 0, 0, 0, 1, 0, 0}, {0, 1, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 
    1, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 0}, {0, 0, 1, 0, 0, 0, 0,
     0, 0}, {0, 0, 0, 0, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 1}};

A1 = T1 . {{1, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 1, 0}, {0, 0, 0}, {0, 
     0, 0}, {0, 0, 1}, {0, 0, 0}, {0, 0, 0}};

A2 = T1 . {{0, 0, 0}, {1, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 1, 0}, {0, 
     0, 0}, {0, 0, 0}, {0, 0, 1}, {0, 0, 0}};

A3 = T1 . {{0, 0, 0}, {0, 0, 0}, {1, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 
     1, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 1}};

Transpose[P1 . ArrayFlatten[{{A1}, {A2}, {A3}}]] == 
  Flatten /@ D[Transpose[Q], {v}] // MatrixForm

Out[26]//MatrixForm= \!\(
TagBox["True",
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)

Is there a neat solution to this problem?

Regards, Zhao