I think that the problem might be that the number of terms in an analytical/symbolic solution of such a system increases dramatically fast.

Try an execute such a problem for small matrices and look at the rapid increase of the cpu time needed:

Table[(Solve[
     Table[Subscript[a, i, j], {i, 1, n}, {j, 1, n}].Table[Subscript[
        x, i], {i, 1, n}] == RandomReal[1, n], 
     Table[Subscript[x, i], {i, 1, n}]] // AbsoluteTiming)[[1]], {n,  2, 5}]

This gives:

{0.000691, 0.007968, 0.127200, 326.635776}

The corresponding figure is:

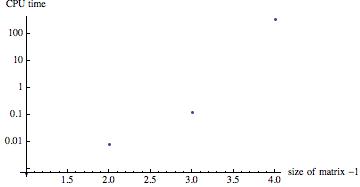
This is because of the number of permutations growing very fast for larger matrix sizes. The solution of linear equations with real entries is much, much faster:

  Table[(Solve[
     Table[RandomReal[], {i, 1, n}, {j, 1, n}].Table[Subscript[x, 
        i], {i, 1, n}] == RandomReal[1, n], 
     Table[Subscript[x, i], {i, 1, n}]] // AbsoluteTiming)[[1]], {n, 2, 30}]

This gives

{0.000247, 0.000217, 0.000246, 0.000277, 0.000378, 0.000461, \
0.000561, 0.000640, 0.000503, 0.000439, 0.000557, 0.000982, 0.000772, \
0.000691, 0.000738, 0.000811, 0.000891, 0.001443, 0.001112, 0.001240, \
0.001318, 0.001424, 0.001646, 0.001748, 0.002253, 0.002522, 0.002084, \
0.002231, 0.002249}

This is very fast so that even very large problems can be handled. Your problem involves the symbolic solution of a 25 times 25 matrix, which should be quite impossible.

M.