By the way, could you please provide the code for scaling the bar? I have a tried, but failed. Thank you!

Glad to help, I'm also glad you caught my error in the first post -- I did not consider the scaling problem (although I have been burned by that multiple times in the past!) Whenever I used a custom color function I frequently had to alter the ColorFunctionScaling to get proper results.

Regards,

Neil

Daniel,

First, to get your bar legend, you need to make a change in syntax:

Plot3D[Re[fun^2 + 1], {x, -2, 2}, {y, -2, 2}, 
 ColorFunction -> Function[{x, y, z}, Hue[Im[(x + y I)^2 + 1]]], 
 PlotLegends -> BarLegend[{Hue, {-4, 4}}]]

As to the Color function, the problem is the default behavior is ColorFunctionScaling->True which scales your x,y, and z to the range 0 to 1. This means that your calculation of Im[fun^2+1] is no longer correct. You need to use ColorFunctionScaling->False, and then you need to scale the values of the argument to Hue to make sense (between 0 and 1). This means you need an offset and scale to Hue to get your function values between 0 and 1. You can automate this easily but the basic plot should look something like this:

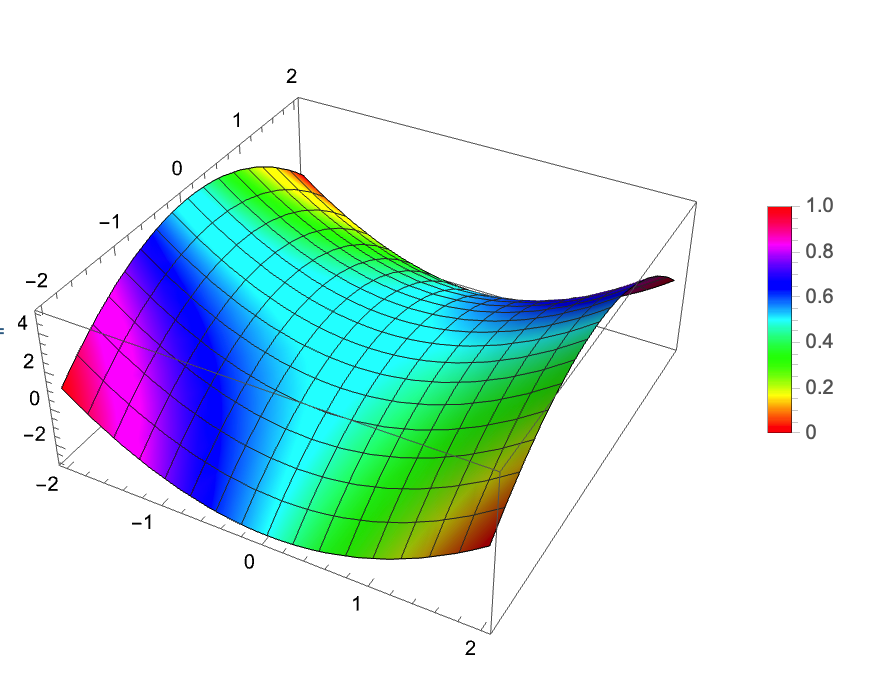
Plot3D[Re[fun^2 + 1], {x, -2, 2}, {y, -2, 2}, 
 ColorFunction -> 
  Function[{x, y, z}, Hue[(Im[(x + y*I)^2 + 1] + 8)/16]], 
 ColorFunctionScaling -> False, PlotLegends -> BarLegend[Hue]]

The legend has the wrong values but you can fix that by creating a function to give to BarLegend that scales the values so the bar is correct.

You get the following:

Regards,

Neil

Daniel,

The problem is syntax:

You entered

ColorFunction -> Function[{x, y, z}, Hue[Im[z^2 + 1]]]

In this function, the x is the real part of z, the y is the Imaginary part of z, BUT z is not your original z its the magnitude of Re[z^2 + 1]. Using z in two places like that is confusing and leads to errors.

You can fix it with:

fun = x + y I;
Plot3D[Re[fun^2 + 1], {x, -2, 2}, {y, -2, 2}, 
 ColorFunction -> Function[{x, y, z}, Hue[Im[fun^2 + 1]]], 
 PlotLegends -> BarLegend[Hue[-4, 4]]]

to get

Regards,

Neil