Regarding the multiplexer that we discussed today. Here is what we wanted to show. Let's construct the following circuit using only operators one by one:
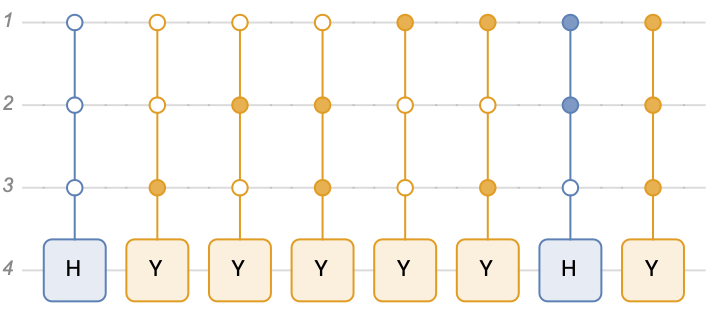
First let's create the correct sequence for control-1 and control-0 qubits:
seq = Reverse[
Values[<|0 -> {}, 1 -> {},
GroupBy[Transpose[{#, {1, 2, 3}}], First -> Last]|>] & /@
Tuples[{0, 1}, 3]]
which gives us:
{{{}, {1, 2, 3}}, {{3}, {1, 2}}, {{2}, {1, 3}}, {{2,
3}, {1}}, {{1}, {2, 3}}, {{1, 3}, {2}}, {{1, 2}, {3}}, {{1, 2,
3}, {}}}
Then the corresponding circuit can be created as follows:
qc = QuantumCircuitOperator[
MapThread[{"C", #2, Sequence @@ #1} &, {Reverse[seq], {"H", "Y",
"Y", "Y", "Y", "Y", "H", "Y"}}]]
once can show that the operator circuit is equivalent to this operator:
QuantumOperator[{"Multiplexer", "H", "Y", "Y", "Y", "Y", "Y", "H",
"Y"}]
Test:
QuantumOperator[{"Multiplexer", "H", "Y", "Y", "Y", "Y", "Y", "H",
"Y"}] == qc["CircuitOperator"]
Of course, note the difference in the number of qudits etc too
