Here is an approach the results in an explicit answer for the pdf of
$\cos(X^2)$ where
$X$ has a normal distribution with mean
$\mu$ and variance
$\sigma^2$.
The pdf has an infinite number of terms but can be approximated well with a finite number of terms.
First solve for
$x$ in
$Cos[x^2]==c$:
Solve[Cos[x^2] == c, x]
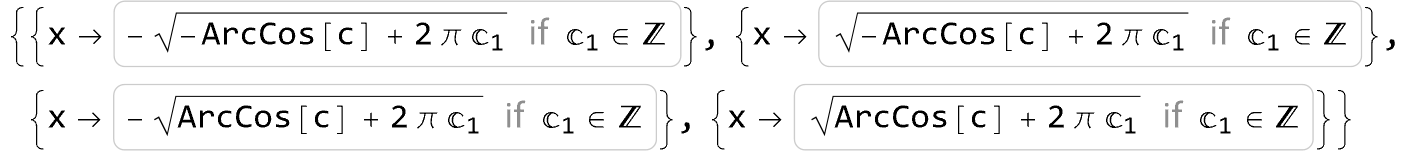
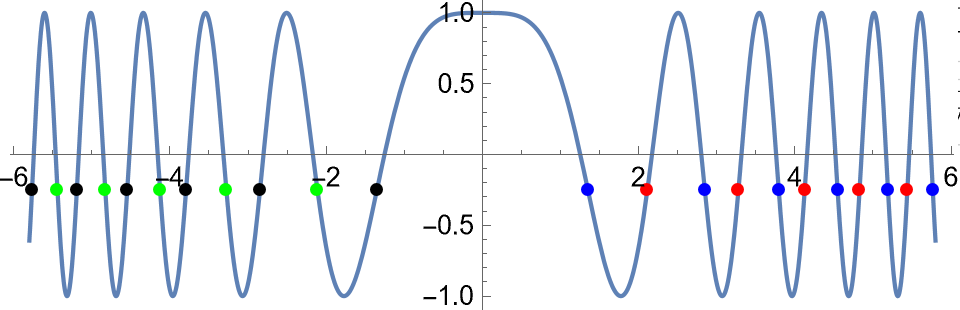
We see that there are a infinite number of values of
$x$ that give the same value of
$\cos(x^2)$. We need to make sure we account for all of those so that we can add up all of the contributions from the pdf of
$X$. Consider
$c=-0.4$:
c0 = -1/4;
Show[Plot[Cos[x^2], {x, -5.8, 5.8}],
ListPlot[Table[{-Sqrt[-ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 1, 5}], PlotStyle -> Green],
ListPlot[Table[{Sqrt[-ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 1, 5}], PlotStyle -> Red],
ListPlot[Table[{-Sqrt[ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 0, 5}], PlotStyle -> Black],
ListPlot[Table[{Sqrt[ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 0, 5}], PlotStyle -> Blue],
AspectRatio -> 1/3]
So for a particular value of c we add up all of the associated density values multiplied by the absolute value of the corresponding Jacobian to obtain the contributions. First the Jacobians:
j1 = D[-Sqrt[-ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]-ArcCos[c]])] *)
j2 = D[Sqrt[-ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]-ArcCos[c]])] *)
j3 = D[-Sqrt[ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]+ArcCos[c]])] *)
j4 = D[Sqrt[ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]+ArcCos[c]])] *)
Now for the pdf of
$\cos(X^2)$:
pdf[c_, \[Mu]_, \[Sigma]_, kmax_] :=
Sum[j1 PDF[NormalDistribution[\[Mu], \[Sigma]], -Sqrt[-ArcCos[c] + 2 \[Pi] k]], {k, 1, kmax}] +
Sum[j2 PDF[NormalDistribution[\[Mu], \[Sigma]], Sqrt[-ArcCos[c] + 2 \[Pi] k]], {k, 1, kmax}] +
Sum[j3 PDF[NormalDistribution[\[Mu], \[Sigma]], -Sqrt[ArcCos[c] + 2 \[Pi] k]], {k, 0, kmax}] +
Sum[j4 PDF[NormalDistribution[\[Mu], \[Sigma]], Sqrt[ArcCos[c] + 2 \[Pi] k]], {k, 0, kmax}]
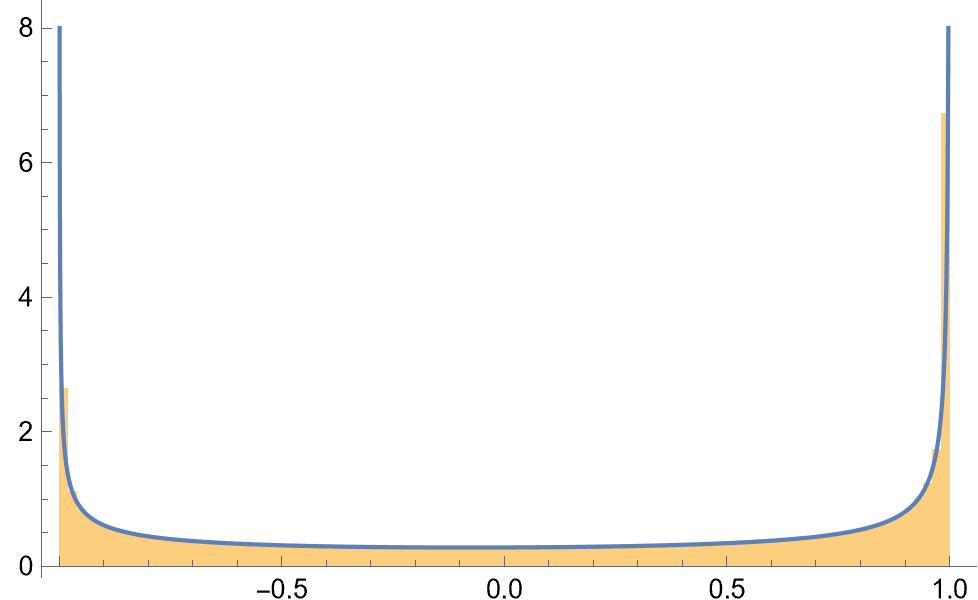
We can check this out with a finite number of terms (i.e., setting kmax to 50 rather than
$\infty$:
SeedRandom[12345];
n = 1000000;
cc = Cos[RandomVariate[NormalDistribution[-2, 3], n]^2];
Show[Histogram[cc, "FreedmanDiaconis", "PDF"],
Plot[pdf[c, -2, 3, 100], {c, -1, 1}, PlotRange -> {{-1, 1}, {0, 8}}]]