For whatever it's worth the second answer followed what's done for a "wrapped normal" distribution.

For the first answer, I chose a 1-to-1 formula and Abs[xx] is not 1-to-1.

Here is an approach the results in an explicit answer for the pdf of $\cos(X^2)$ where $X$ has a normal distribution with mean $\mu$ and variance $\sigma^2$.

The pdf has an infinite number of terms but can be approximated well with a finite number of terms.

First solve for $x$ in $Cos[x^2]==c$:

Solve[Cos[x^2] == c, x]

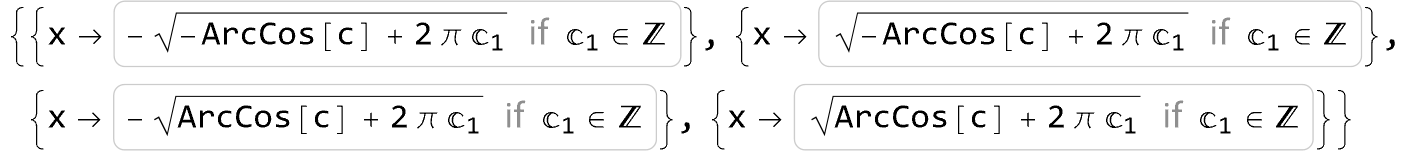
We see that there are a infinite number of values of $x$ that give the same value of $\cos(x^2)$. We need to make sure we account for all of those so that we can add up all of the contributions from the pdf of $X$. Consider $c=-0.4$:

c0 = -1/4;
Show[Plot[Cos[x^2], {x, -5.8, 5.8}],
  ListPlot[Table[{-Sqrt[-ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 1, 5}], PlotStyle -> Green],
  ListPlot[Table[{Sqrt[-ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 1, 5}], PlotStyle -> Red],
  ListPlot[Table[{-Sqrt[ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 0, 5}], PlotStyle -> Black],
  ListPlot[Table[{Sqrt[ArcCos[c] + 2 \[Pi] k], c} /. c -> c0, {k, 0, 5}], PlotStyle -> Blue],
  AspectRatio -> 1/3]

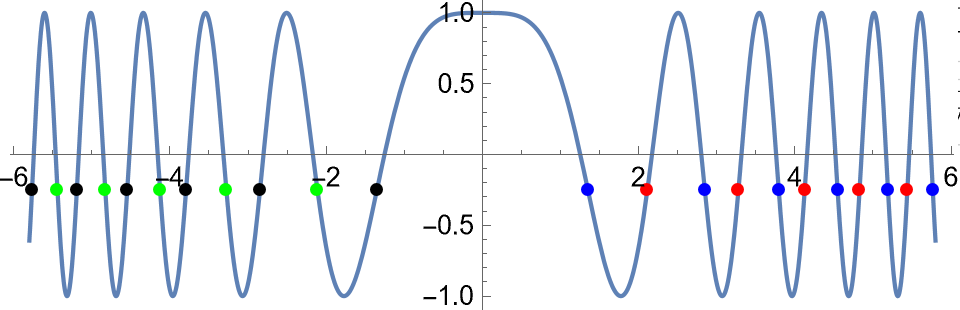
So for a particular value of c we add up all of the associated density values multiplied by the absolute value of the corresponding Jacobian to obtain the contributions. First the Jacobians:

j1 = D[-Sqrt[-ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]-ArcCos[c]])] *)
j2 = D[Sqrt[-ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]-ArcCos[c]])] *)
j3 = D[-Sqrt[ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]+ArcCos[c]])] *)
j4 = D[Sqrt[ArcCos[c] + 2 \[Pi] k], c] // Abs
(* 1/2 Abs[1/(Sqrt[1-c^2] Sqrt[2 k \[Pi]+ArcCos[c]])] *)

Now for the pdf of $\cos(X^2)$:

pdf[c_, \[Mu]_, \[Sigma]_, kmax_] :=
 Sum[j1 PDF[NormalDistribution[\[Mu], \[Sigma]], -Sqrt[-ArcCos[c] + 2 \[Pi] k]], {k, 1, kmax}] +
  Sum[j2 PDF[NormalDistribution[\[Mu], \[Sigma]], Sqrt[-ArcCos[c] + 2 \[Pi] k]], {k, 1, kmax}] +
  Sum[j3 PDF[NormalDistribution[\[Mu], \[Sigma]], -Sqrt[ArcCos[c] + 2 \[Pi] k]], {k, 0, kmax}] +
  Sum[j4 PDF[NormalDistribution[\[Mu], \[Sigma]], Sqrt[ArcCos[c] + 2 \[Pi] k]], {k, 0, kmax}]

We can check this out with a finite number of terms (i.e., setting kmax to 50 rather than $\infty$:

SeedRandom[12345];
n = 1000000;
cc = Cos[RandomVariate[NormalDistribution[-2, 3], n]^2];

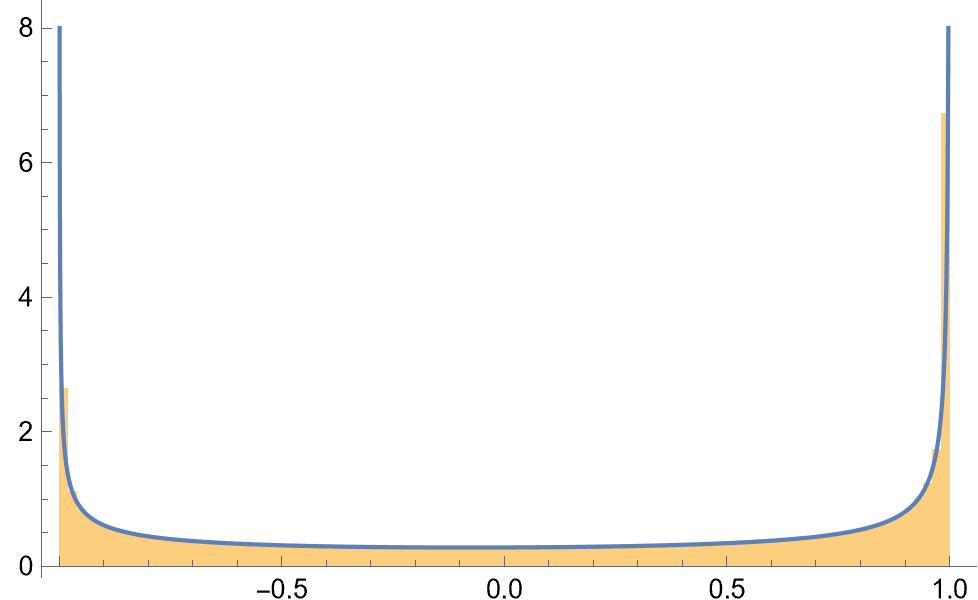
Show[Histogram[cc, "FreedmanDiaconis", "PDF"],
 Plot[pdf[c, -2, 3, 100], {c, -1, 1}, PlotRange -> {{-1, 1}, {0, 8}}]]

As Eric Rimbey mentions TransformedDistribution is the function to try. However, in this case Mathematica does not find a pdf (and a closed-form might not even exist).

The next thing to try is to take a large sample and look at the resulting shape of the distribution. In this case, it appears that a beta distribution might provide a good fit (but properly scaled to have values between -1 and 1).

dist = TransformedDistribution[Cos[x^2], x \[Distributed] NormalDistribution[-2, 3]];
xx = RandomVariate[dist, 10000000];

(* Scale xx to be between 0 and 1 *)
z = (1 + xx)/2;

(* Solve for the corresponding moments of a beta distribution *)
sol = Solve[{Mean[z] == Mean[BetaDistribution[a, b]],
    Variance[z] == Variance[BetaDistribution[a, b]]}, {a, b}][[1]]
(* {a -> 0.485618, b -> 0.369652} *)

(* Show results *)
Show[Histogram[xx, "FreedmanDiaconis", "PDF"],
 Plot[PDF[BetaDistribution[a, b] /. sol, (1 + x)/2]/2, {x, -1, 1}, PlotRange -> {{0.01, 0.99}, {0, 8}}]]